凸凹性等几何性质研究

§3.6　函数的单调性、凸凹性等几何性质研究

知识点：1．单调性判别法。

　　　　2．极值的必要条件、充分条件。

　　　　3．凸凹性和拐点

　　　　（1）定义式；（2）几何式定义法（割线、切线）；（3）f′（x）单调；（4）f″（x）保号。

　　　　4．渐近线（铅垂渐近线、水平渐近线、斜渐近线）：

　　　　若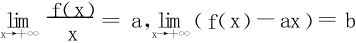，都存在，则y＝ax＋b是曲线y＝f（x）的渐近线。

　　　　5．函数作图，基本步骤如下：

　　　　（1）确定定义域，奇偶性，周期性，连续性；

　　　　（2）求f′（x），确定驻点和不可导点，求出单调区间和极值；

　　　　（3）求f″（x），确定凸凹区间和拐点（列一个表格）；

　　　　（4）求渐近线；

　　　　（5）再描若干个特殊点（如和坐标轴的交点等等）。

例1　设定义于［a，b］上的函数具有介值性，且f在（a，b）内可微，导函数有界，则f（x）必然在［a，b］连续。

分析　关键证在端点处的单边连续性，f在（a，b）上连续，可微，且导函数有界，故f必在（a，b）上有界，那么f（（a，b））是不是一个区间呢？

证明　依题意，∃M>0，st｜f′（x）｜≤M，x∈（a，b）

∀ε>0，取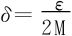。不妨设f在［a，a＋δ］上不恒为常数。

由介值性知∃r∈（a，a＋δ），使。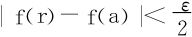

于是∀x∈（a，a＋δ），有

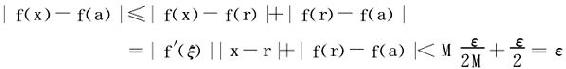
故f（x）在a点右连续。在b点左连续的证明完全类似。读者不妨一试。

例2　设x>0，求证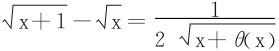，其中θ（x）满足

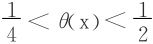
证明　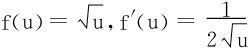，对f（u）在区间［x，x＋1］上用L-中值定理知∃0<θ<1，st

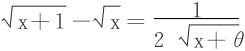
以下主要证明。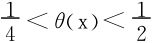

从上式解出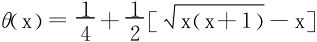，易知

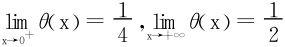
下证θ（x）单调增

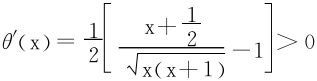
故θ（x）在（0，∞）上严格增加，进而有。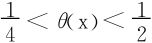

例3　f（x）在［0，c］上可微，f′（x）在［0，c］上单调减，f（0）＝0，试证

∀0≤x₁<x₂<x₁＋x₂≤c有f（x₁＋x₂）≤f（x₁）＋f（x₂）

证　欲证不等式移项并利用f（0）＝0，得

f（x₁＋x₂）－f（x₂）≤f（x₁）－f（0）

由L-中值定理知∃ξ₁∈（0，x₁），ξ₂∈（x₂，x₁＋x₂），st

f（x₁＋x₂）－f（x₂）＝f′（ξ₂）x₁，f（x₁）－f（0）＝f′（ξ₁）x₁。

利用f′（x）的递减性有f′（ξ₁）≥f′（ξ₂），立得所要证明不等式。

例4　设函数y＝y（x）由隐函数方程2y³－2y²＋2xy－x²＝1决定，试求y＝y（x）的驻点并判定其是否为极值点以及最值点。

解　用隐函数微分法，求出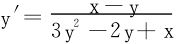，令y′＝0，得x＝y

代入原方程，解出驻点x₀＝1，用二阶导数来判断x₀＝1是否极值点

（3y²－2y＋x）y″＋y′（6yy′－2y′＋1）＝1－y′

例5　已知a>0，曲线f（x）＝ax－（1＋a⁴）x³与轴交于点（c，o），其中c>0。问a取何值时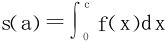，最大？

解　解出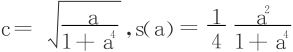

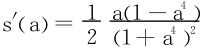，令s′（a）＝0，得a＝0，±1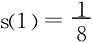，为最大值。

例6　已知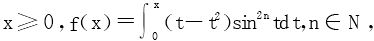证明

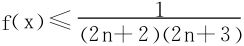
证　f′（x）＝（x－x²）sin²ⁿx，稳定点为x＝0，1，kπ，（k∈N），不难判定x＝1是唯一的极大值点，x>1时，f′（x）<0，x<1时，f′（x）>0，故f（1）也是最大值。

所以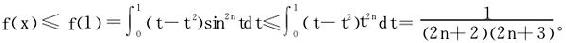　

例7　设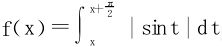，求f的最值。

解　首先确定f是周期π的函数，故只需在［0，π］上求最值。又

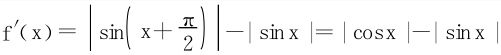
得稳定点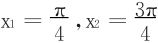，比较大小，f（0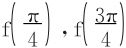），，f（π），得知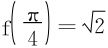为最大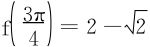值，为最小值。

例8　分别讨论函数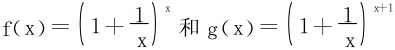在R^＋上的单调性。

解　先讨论f（x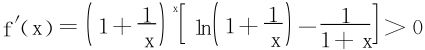）。，从而f（x）增加。

注　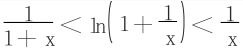是一个较常用的不等式，可以用微分中值定理推出

结合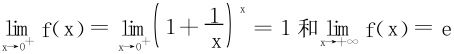，知1<f（x）<e。

再讨论g（x），类似求得

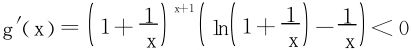
于是g（x）在R^＋单调递减。又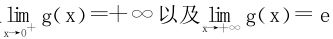，知g（x）>e恒成立。

例9　考虑一般含参数a的函数簇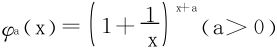的单调性。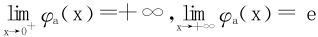，若φa（x）单调减，则一定有φ（x）>e。

关键技术：不等式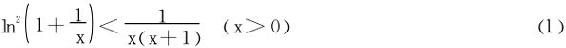

此不等式的证明参阅下一节（§3.7）的例2。

解法一　不等式等价变形，突出a的地位，类似于例2中对θ（x）的讨论。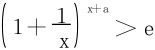两边取对数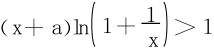，，得

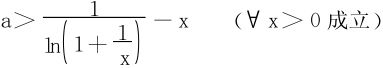
令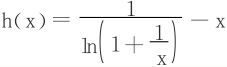，只须求出h（x）在（0，＋∞）的上确界或最大值。

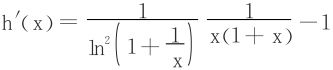
结合上述基础不等式（1）知h′（x）>0，故h（x）在（0，＋∞）上递增

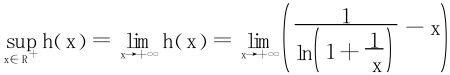
（此为∞－∞型不定式，通分后用洛必达法则显然麻烦，故采用变量代换，令）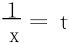

或进行Taylor展开，

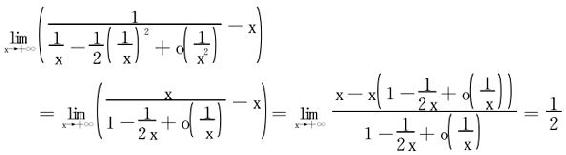
解法二　分析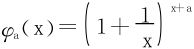的单调性，或说求最小的能使φ_a（x）单调减的a的值。

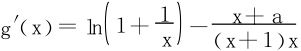（a＝0，1时例8已经讨论清楚）

希望g′（x）<0对x>0成立，即

若已知有不等式（1），则（2）成立的充分条件是

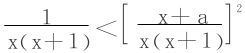
即等价于

x（x＋1）<（x＋a）²　∀x>0

于是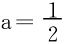时，（2）式一定成立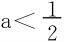；时，（2）式一定不恒成立。

若不知有不等式（1）又该如何？

分析　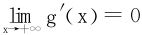，欲要g′（x）从x轴下方趋于0，相当于

g′（x）是单调增加，于是再求。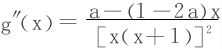

欲使g″（x）>0，（∀x>0），则当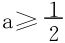时，恒成立。

上面分析说明了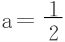，可以使φ_a（x）单调递减。

如何说明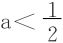时，原不等式不能对于所有的x>0恒成立呢？

分析　当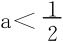时，∃x₀>0，st　g′（x₀）＝0，即

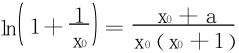
此时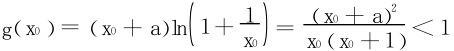

所以φ（x₀）＝e^g（x₀）<e，证毕。

补充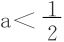：时，求得g″（x）的零点是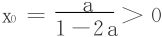。0<x<x₀时，g″（x）>0；x₀<x<∞时，g″（x）<0。即在（0，x₀）上，g′（x）↗，（x₀，∞）上，g′（x）↘。x₀是g′（x）的最大值点。结合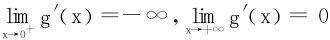，一定∃x^*∈（0，x₀），st　g′（x^*）＝0，0<x<x^*时，g′（x）<0，即得g（x）从而φ_a（x）在（0，x^*）上递减；x^*<x<∞时，g′（x）>0，g（x）从而φ_a（x）在（x^*，∞）上递增。能在R^＋上保持纯递增的函数只有a＝0时一个。

（因为a>0时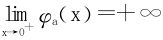，，故φ_a（x）无法递增）

解法三　欲要g（x）>1，即得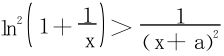因

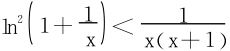
又得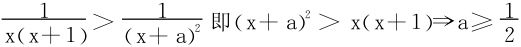

（此为g（x）>1∀x>0成立的必要条件）

再证亦是充分条件当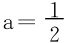时，令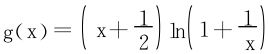，如解法二得g′（x）<0，所以g（x）>g（＋∞）＝1。

或等价于证明：

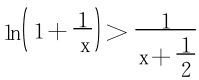
取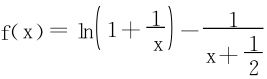

求得f′（x）<0，又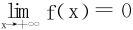，所以f（x）>0得证。

思考题：求最大的α，使得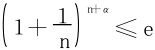对所有整数n成立。或更一般地，给出集合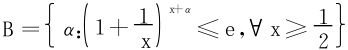，求B的最大元。

例10　设f（x）在x＝x₀处存在n阶导数，且f^（k）（x₀）＝0，（1≤k≤n－1），f^（n）（x₀）≠0。试证

（1）n为奇数时，f（x₀）不是极值；

（2）n为偶数时，则当f^（n）（x₀）<0时，f（x₀）为极大值；

　　　　　　　　　　f^（n）（x₀）>0时，f（x₀）为极小值。

联想：极值的第二充分条件。

证明　由Taylor展开（带皮亚诺余项）

（此式类似于微分式（n＝1时））。

推广：二元函数的Taylor展开和极值判定。

定理1　若函数f（x，y）在点P₀（x₀，y₀）的某邻域内有直到n＋1阶连续偏导数，则对邻域内任一点P（x₀＋h，y₀＋k），∃0<θ<1，st

定理2　设f（x，y）在P₀的邻域内有二阶连续偏导数，且P₀为f的稳定点，即f_x（P₀）＝f_y（P₀）＝0，引入A＝f_xx（P₀），B＝f_xy（P₀），C＝f_yy（P₀），Δ^*＝AC－B²，则

Δ^*<0时，P₀不是极值点；

Δ^*>0时，P₀是极值点：A>0时为极小，A<0时为极大。

证明　依皮亚诺余项的Taylor展开公式以及f_x（P₀）＝f_y（P₀）＝0，

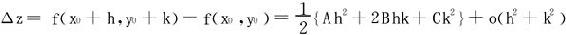
记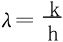，则λ∈R

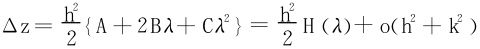
Δz的符号取决于H（λ）的符号，当H（λ）的判别式Δ＝－4Δ^*<0时，H（λ）保号，此时相当于Δ^*>0，于是z＝f（x，y）有极值。

例11　若f（x）在R上三阶连续可导，且∀h>0，有

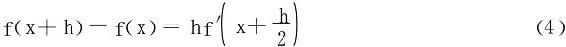
证明函数f（x）是至多二次多项式。

分析思路　若f（x）是二次多项式，则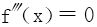，对二次多项式，自然满足（4）式

证一　由Taylor展开，对f（x＋h）在x处展开至二阶

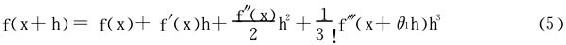
对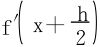在x处展开（至一阶）：

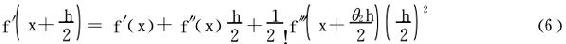
利用条件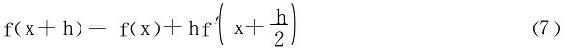　

将（6）代入（7）并与（5）式比较（两式相减），得知

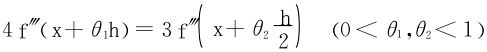
证二　（4）式等价于f（x＋h）－f（x－h）＝2hf′（x）

对h求导两次得f″（x＋h）＝f″（x－h），再令x＝h得f″（2x）＝f″（0）为常数。

证三　（4）式两边对h求导，，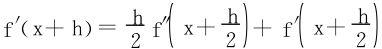

令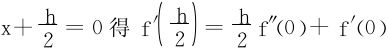。再在（4）中令x＝0，得

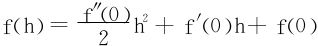，证毕。

例12　凸函数不等式，若函数f（x）在（a，b）内二阶可微，f″（x）>0，则对于（a，b）内任意n个点x₁，x₂，…，x_n恒有

等号成立当且仅当诸x_i相同。

证明　令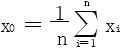，将f在x₀处展开为：

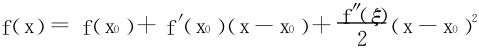　（ξ介于x₀，x之间）

分别以x₁，x₂，…，x_n代入上式，得到f（x_i）≥f（x₀）＋f′（x₀）（x_i－x₀），i＝1，2，…，n诸式相加即得欲证之结论。

注　f″（x）>0是f为（a，b）上严格凸函数的充分条件，对于严凸函数，其定义式是

∀x₁<x₂，x₁、x₂∈（a，b），0<λ<1，恒成立

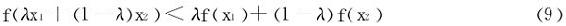
对于凸函数从归纳法（纯初等推导）可得出Jensen不等式：

证明　用归纳法。关键步骤：n＝k＋1时

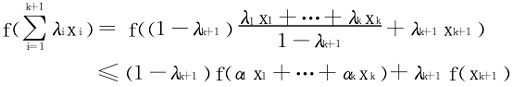
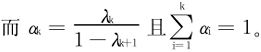
自然用Taylor展开的方法一样可证，只需在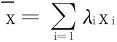处作Taylor展开。

推广：若φ（t）在［0，a］连续，f二阶可导，且f″（x）≥0，则有

首先要明了，积分是离散求和的拓广，即无穷微分之和。从本质上讲，（11）式和（8）式是同源的，如何证呢？

（11）式相当于

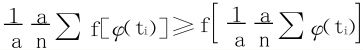
视x_i＝φ（t_i）就是（8）式，故成立，然后令n→∞，过渡到（11）。

证二　记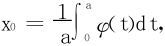将f（x）在x₀近旁作Taylor展开：

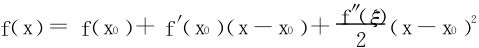
由于f″（x）≥0，故f（x）≥f（x₀）＋f′（x₀）（x－x₀）

两边以x＝φ（t）代入：

f［φ（t）］≥f（x₀）＋f′（x₀）［φ（t）－x₀］

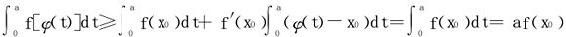
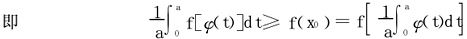
习题3.6

1．若f（x）为［a，b］上正值连续函数，则有

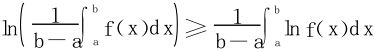
2．若f（x）在［0，1］上二阶可导，f″<0，证明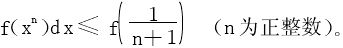

3．设f（x）在R上二阶连续可导，且

xf″（x）＋3x（f′（x））²＝1－e^－x

　（1）若f（x）在x＝c（c≠0）处有极值，证明该极值是极小值；

　（2）若f（x）在x＝0处有极值，它是极小值还是极大值？为什么？

4．设g（x）在［a，b］连续，在（a，b）内二阶可导，且｜g″（x）｜≥λ>0，g（a）＝g（b）＝0。

　证明

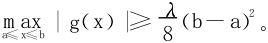
5．设f（x）在［a，b］上二阶导数连续，f″（x）≤0，证明。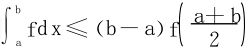

6．设f（x）在R上三阶可导，并且f和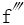有界，证明f′和f″也有界。

7．设f在（a，＋∞）二阶连续可导，且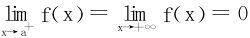。证明

　（1）∃x_n∈（a，＋∞），x_n→＋∞，；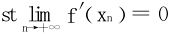

　（2）∃ξ>a　st f″（ξ）＝0。

8．设f（x）在［0，＋∞）上一阶可微，且f（0）＝0，f′（x）在（0，＋∞）上单调递减。试证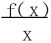也在（0，＋∞）上单调递减。

（中科院1985年）

（南开大学1982）