§4.5 定积分不等式
一、基本不等式及其证明
H lder不等式 设p、q>1且
lder不等式 设p、q>1且 (此p、q被称为共轭指数),则有
(此p、q被称为共轭指数),则有

引入记号  (Lp空间的范数),则H
(Lp空间的范数),则H lder不等式可以写成
lder不等式可以写成

特例当p=q=2时,得出柯西-许瓦兹不等式。
闵可夫斯基不等式 设f,g∈Lp,p≥1,则有如下的三角不等式

W·H·Young不等式 设f(x)在[0,∞)上连续且递增,f(0)=0,a,b>0,f-1(y)为f(x)的反函数,则有

分析 几何意义
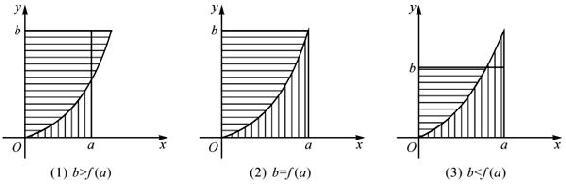
图4-2
从图形4-2易知等号当且仅当f(a)=b时成立。
凸函数不等式 设f(x)∈R[a,b],且m≤f(x)≤M,φ(u)是[m,M]上的下凸函数,则有

即积分平均值的一个关系式:

此处 表示函数f在[a,b]上的积分平均值,
表示函数f在[a,b]上的积分平均值,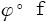 表示复合函数φ(f(x))。
表示复合函数φ(f(x))。
比较离散情形的凸函数不等式

或 φ(∑λixi)≤∑λiφ(xi) (其中λi≥0且∑λi=1)
若离散型的公式记牢,连续情形的公式就易记。
推广:p(x)>0,则有
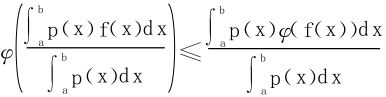
证明思路回顾(参见本书§3.6例12之推广,稍加注意的是那里的函数记号和现在略有不同)。
法一 从Riemann积分定义出发,对[a,b]等分,离散型不等式→连续型不等式。
法二 Taylor展开方法,记 ,将φ在u0处作Taylor展开,并利用φ(u)的凸性。(此时要求φ(u)是二阶可导函数,φ(u)≥φ(u0)+φ′(u0)(u-u0))。
,将φ在u0处作Taylor展开,并利用φ(u)的凸性。(此时要求φ(u)是二阶可导函数,φ(u)≥φ(u0)+φ′(u0)(u-u0))。
延伸:当φ(u)是凹函数时,不等式(4)要反向。
又特取φ(u)=lnu,φ(u)=eu等等时,得到一些特殊的不等式,如
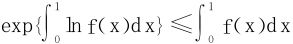 ,其中f(x)为正值连续函数。
,其中f(x)为正值连续函数。
例1 H lder不等式的证明
lder不等式的证明
(1)加权幂平均≤加权和平均 
(2)单位化 令f1=f/‖f‖pg1=g/‖g‖q,则‖f1‖p=‖g1‖q=1。
先证明 。参见§3.7之例11。
。参见§3.7之例11。
例2 minkowski不等式:设f,g∈Lp(p≥1),则有‖f+g‖p≤‖f‖p+‖g‖p。
对|f|和|f+g|p/q应用H lder不等式得
lder不等式得

同理

两式相加,得(因为p-1=p/q)

minkowski不等式当p=q=2时即为Cauchy-Schwarz不等式,此不等式还有一个简易的证明方法,令u(x)=[f(x)-λg(x)]2≥0,则 ,即
,即 ,∀λ∈R成立。
,∀λ∈R成立。
由二次三项式的判别式Δ≤0立得欲证之不等式。
例3 Young不等式的证明
(i)当f(a)=b时,要证的不等式转化为

几何意义非常明显,见图4-2-(2)。
若加强条件f(x)连续可微,可用常数变易法证得(3′),视a为变量t,一般情形,可用定积分定义。
f(x)在[0,a]上连续且↗,则f(x)在[0,a]上一致连续。又得f-1(y)在[0,f(a)]上连续且↗。将[0,a]n等分0=x0<x1<…<xn=a,相应地0=y0<y1<…<yn=f(a)。当n→+∞时, 。
。
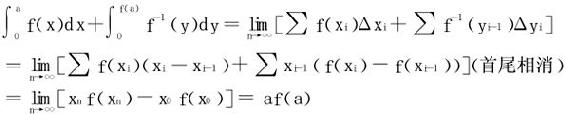
(ii)当b<f(a)时,不妨设b=f(x*),x*<a
从(i)知

所以

(iii)当b>f(a)时,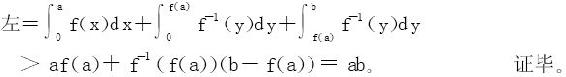
特取f(x)=xp-1,当p>1时,满足Young不等式的要求f-1(y)=yq-1,可得

这个不等式在§3.7例12证明H lder不等式时曾被引用。
lder不等式时曾被引用。
二、积分不等式的证明方法
1.利用基本不等式法
例4 假设f∈C[a,b],f(x)>0,证明 。
。
证明 利用Cauchy-Schwarz不等式
例5 设fi(x)(i=1,2,…,n)恒正连续,证明

(当n=2时,即为Cauchy不等式)
证明 单位化,引入
原不等式化为 
因为 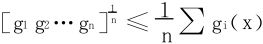
所以 
注 此证法本质即为将不等式的右边去除左边,起化简作用。
不等式的变形:fi(x)不一定非负时,可以用|fi|代替fi。
又将开方转换成乘方形式:

再在(5′)中令f1(x)=f(x),f2=…=fn=1,得出

上述不等式可以简写为

事实上,由不等式(4),取φ(u)=un亦可得到不等式(6)。
例6 设f为[a,b]上连续正值函数,讨论f的n次幂平均序列Jn(f)之单调性和极限。
解 取 ,q=n+1,则p,q为共轭指数,利用H
,q=n+1,则p,q为共轭指数,利用H lder不等式
lder不等式
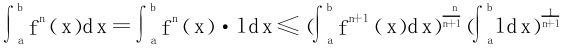
于是

故Jn(f)单调递增,下面考虑Jn(f)当n→+∞时的极限。因f∈C[a,b],f(x0)=M为f的最大值,Jn(f)≤M较明显。
∀ε>0,∃δ>0,stU(x0;δ)⊂[a,b](当x0即为端点时,U(x0)取单边邻域)且x∈U(x0;δ)时,M-ε≤f(x)≤M

得知

于是

2° 在相同条件下, 。如
。如 。剖析此结果
。剖析此结果

那么应该有

记 
易得

相乘知 。所以
。所以 ,得印证。
,得印证。
2.常数变易法
一个常量的问题,如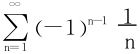 的求和等,必得借助于引入适当的变量,如幂级数
的求和等,必得借助于引入适当的变量,如幂级数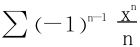 ,采用逐项求积分或逐项求微分等等技术求得其和。这个变量的引入,恰如分牛问题:某农户有十七头牛,三个儿子分,大儿子得
,采用逐项求积分或逐项求微分等等技术求得其和。这个变量的引入,恰如分牛问题:某农户有十七头牛,三个儿子分,大儿子得 ,二儿子得
,二儿子得 ,三儿子得
,三儿子得 。如何实施分割呢?只需借一头牛,则三个儿子依次各分得9头,6头,2头,仍多出一头牛。这借来的一头号牛其实只是虚晃一枪,这就是数学的智慧。
。如何实施分割呢?只需借一头牛,则三个儿子依次各分得9头,6头,2头,仍多出一头牛。这借来的一头号牛其实只是虚晃一枪,这就是数学的智慧。
在Young不等式的证明中,我们也已经提及常数变易法。
例7 假定f(x)在[0,1]上单调递减,试证∀a∈(0,1)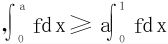 。
。
证一 引入 ,转换命题证明H(a)≥H(1)
,转换命题证明H(a)≥H(1)
这由f(x)在[0,1]上的递减性不难推得
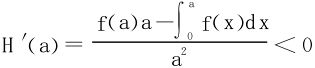
证二 分析法,欲证原不等式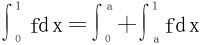
得出原不等式等价于

而f(x)↘,故必有

证三 令x=αt,则
例8 假定f∈C′[0,1],且0<x<1时,0<f′(x)<1,f(0)=0,试证

证一 令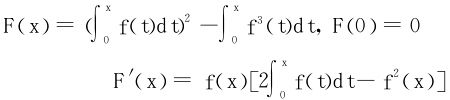
记
证二 令 作比法且由Cauchy微分中值定理∃ξ∈(0,1)以及η∈(0,ξ)使得
作比法且由Cauchy微分中值定理∃ξ∈(0,1)以及η∈(0,ξ)使得

3.升维法
通常高维的问题须降维,如化二重积分为累次积分。但偶尔也有例外,如广义积分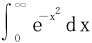 的求值,就可采用升维技术先转化为第一象限的二重积分再利用极坐标变换求之。同样地,在不等式的证明方面,升维亦能起到柳暗花明的独特作用。
的求值,就可采用升维技术先转化为第一象限的二重积分再利用极坐标变换求之。同样地,在不等式的证明方面,升维亦能起到柳暗花明的独特作用。
例9 设f,g是[a,b]上严格递增的连续函数,则有
证明 作差法令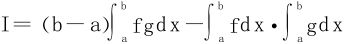
作以下升维变形:记D=[a,b]×[a,b]
由对称性

于是
或:(f(x)-f(y))(g(x)-g(y))≥0称f,g为似序的。
上式先对x积分,后对y积分。
例10 设f(x)∈C[0,1]且严格递增,证明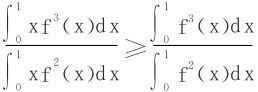
证 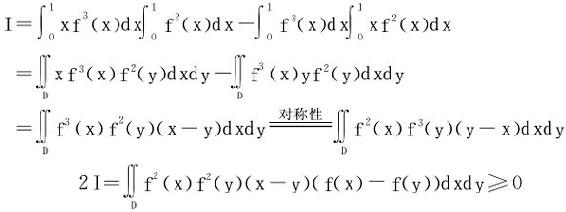
习题4.5
1.证明当a,b≥1时,ab≤ea-1+blnb。(f(x)=ex-1,Young不等式)
2.f(x)在[0,1]上非负连续,单减,0<a<b<1,证明:

3.设f∈C[0,1],证明

4.设p(x)为[a,b]上的正值可积函数,f,g是[a,b]上的不减函数,则有:
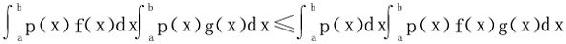
5.设f(x)是在[a,b]上的正值连续函数,试求 。或f的n次幂平均Jn(f)中,允许n取负整数时,考虑Jn(f)的单调性和极限
。或f的n次幂平均Jn(f)中,允许n取负整数时,考虑Jn(f)的单调性和极限 (n从-1,-2,…,往下取时,J-1(f)>J-2(f)>J-3(f)>…)
(n从-1,-2,…,往下取时,J-1(f)>J-2(f)>J-3(f)>…)
6.设f(x),g(x)都是连续且非负,则 。若记
。若记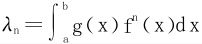 ,证明
,证明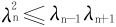 ,进而
,进而 存在。
存在。
8.设f在[a,b]上连续、正值,则 。
。
9.设f在[0,1]上连续且0≤f<1。证明

10.设x>0时f0(x)>0,定义 证明nfn+1(x)<xfn(x)。
证明nfn+1(x)<xfn(x)。
11.设f(x)、g(x)在[0,1]上的导数连续,且f(0)=0,f′(x)≥0,g′(x)≥0。证明:对任何a∈[0,1]有

(2005年数学(三))
12.设f在[a,b]上连续、单调递增。证明 。并且等号仅当f为常值时成立。
。并且等号仅当f为常值时成立。
(北师大2004年)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















