偏微分方程及其变换

§6.4　偏微分方程及其变换

变量代换思想在数学中广泛应用，体现了一种转化矛盾，从繁到简直至解决问题的思路。无论在求极限，还是求积分包括二重、三重积分等问题，经常要使用变量代换。同样，对一个包含未知函数偏导数的方程，适当地引入变换，就可以使方程得以简化进而求得其解。

现设有二元函数z＝f（x，y），满足一个偏微分方程（一阶或二阶）

引入变换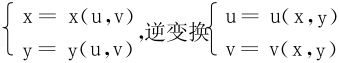

称（u，v）为新变量，（x，y）为原变量，我们面临的任务是要将关于原变量x，y的方程变换为关于新变量u，v的新方程，或是证明一个新旧变量之间的偏导数恒等关系。

如何实现偏导数之间的变换呢？一个基本的工具是链式法则，解题时须特别留意变换的方向选择。通常我们视z是以x，y为中间变量以u，v为自变量的复合函数

依链式法则：

或若视（u，v）为中间变量，x，y为自变量，于是有

将x＝x（u，v），y＝y（u，v）都用u，v表示。代入上式，以及原偏微分方程，就可以得关于（u，v）变量的新的偏微分方程。

例1　证明：在变换u＝x，v＝x²＋y²下，方程

可转化成

证一

代入原方程立得

证二　因为已告知目标方程为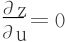，我们也可以采用执果索因证法，视（u，v）为自变量，（x，y）为中间变量。

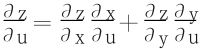
从原变换易解出

（如不去解逆变换，则可以使用反函数组的求导法，解出）

故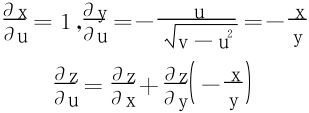　

所以方程即化为

注　1．证明时可以从原方程出发，也可以从新方程出发，原则上可以选择从较简的一个方程出发。

2．证明时应选用偏导数易算的变换式，如极坐标变换就应视（r，θ）为新变量，（x，y）为中间变量。

然后容易证明

3．变换后得以简化的方程往往极易求解。

由于的解是z＝g（v）即得微分方程的通解是z＝g（x²＋y²）。可以说微分方程变换的目的仍是求解微分方程。

解　因为变换后的新方程未知，我们只能从原方程出发，视（x，t）为自变量，（u，v）为中间变量。

代入原弦振动方程化简得以u，v为变量的新方程是，进而易求得此方程的解为φ＝f（u）＋g（v），从而原方程解的形式为φ（x，y）＝f（x＋at）＋g（x－at）。

还有一类题型是除了自变量变换外，因变量（函数）亦同时代换，要求出新函数对新变量的偏导数所满足的方程。为求出此方程，将新函数看成通过中间变量（新变量）而为原变量的函数，并实施以下步骤：

（1）在新函数表示式两端分别对原变量求偏导数；

（2）解出原函数对原变量的一阶偏导数的表示式；

（3）再求出其二阶偏导的表示式；

（4）将它们代入所给出的原方程，化简整理即可得到新函数对新变量的偏导数所满足的方程。

例3　设函数z＝z（x，y）满足方程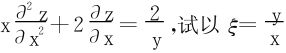，η＝y为新的自变量，w＝yz－x为ξ，η的函数，把方程变换为w＝w（ξ，η）所满足的方程。（浙江大学2001年）

解　在w＝yz－x的两边都对x求偏导：

以代入上式可解得

上式再对x求偏导：

代入原方程并化简得

思考　上述方程的解如何？

例4　设u＝u（x，y）可微，在极坐标变换之下，，证明：

证一　从左往右证

u可以看作r，θ的复合函数，即以x，y为中间变量。

证二　从右往左证，即视r，θ为中间变量。

如何求呢？

若从极坐标变换解出逆变换

得到。

但一般而言，我们不必去显化，而直接依赖隐函数的微分技巧。

对

即得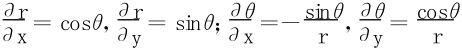

所以　

从而易验证　

注　在原极坐标变换中，r、θ处于自变量地位，从而在变换之时，将x，y视作中间变量的方法（从左往右化简）更显简单。

例5　设n为正整数，若∀t>0，f（rx，ty）＝tⁿf（x，y），称f是n次齐次函数。证明：若f可微，则f是n次齐次函数的充要条件是

证明　必要性：在f（tx，ty）＝tⁿ（f（x，y）的两边关于t求导。

f′₁·x＋f′₂·y＝nt^n－1f（x，y），令t＝1立得（*）式

充分性：

先讨论n＝0时，f（tx，ty）＝f（x，y）

令。

令变量代换，并以ξ，η为中间变量：

于是　

原微分方程化简为，从而g（ξ，η）＝g（η），即有。

以下讨论一般情形

在f（tx，ty）＝tⁿf（x，y）中令，可得

于是引入中间变量ξ＝xⁿ，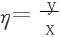

原方程

因为这个方程只含有ξ和u，而不含有η，故可视η为参量，改而求解常微分方程，得出u＝Cξ。

但此中常数C应是可以依赖于η的，记C＝F（η），得到

得知u＝f（x，y）为n次齐次函数。

例6　若u（x，y）的二阶导数存在，证明u（x，y）＝f（x）g（y）的充要条件是

（清华大学）

证一　只证充分性，回忆二阶常微分方程y″＝f（x，y′）及y″＝f（y，y′）的降阶解法。

现令，原方程化为。

视x为参量，y为变量。（亦即将上述方程视为常微分方程）

分离变量：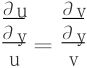

上式两边关于y积分：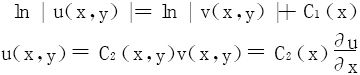

再分离变量：

两边关于x积分：

证二　从

等价化为

即　，上式凑微分又得

　　

解得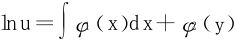　

从而　

习题6.4

1．设变换u＝x－2y，v＝x＋ay可把方程化为，试求a。

（1996年（数学一））

2．证明：在变换ξ＝x，之下，方程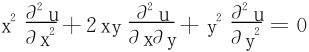可以化为。进而求解此方程。

3．在极坐标变换下，证明

4．给出变换

5．设u＝x＋y，。变换方程

6．设z＝f（x－y，x＋y）＋g（x＋ky），f、g具有二阶连续偏导数，且，如果，求常数k的值。

（浙江省高等数学竞赛2005）

7．令，变换方程。

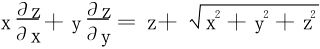
（北师大2001年）

8．已知z＝z（x，y）满足微分方程

　引入变换，ξ＝x²－y²，η＝y，将上述方程变换为关于ξ，η的形式，然后求解之。

9．若u＝f（x，y）满足拉普拉斯方程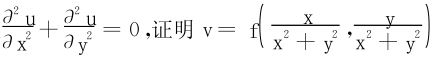也满足此方程。

10．若三元函数f（x，y，z）可微，证明f为n次齐次函数的充要条件是

11．设Ω为含原点的凸区域，u＝f（x，y）在Ω上可微，且满足。

　求证：f（x，y）在Ω上恒为常数。

12．试求在球面坐标变换之下的新形式。

13．证明拉普拉斯算子在柱面坐标（r，θ，z）下可以写成

14．证明在球面坐标变换x＝rsinφcosθ，y＝rsinφsinθ，z＝rcosφ之下，

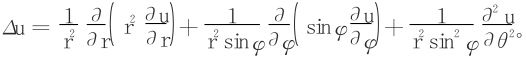
15．设z＝z（x，y）在R²上一阶连续可偏导，w＝w（u，v）由方程组u＝x²＋y²，，z＝e^w＋x＋y所确定，试将方程

　化为所满足的关系式。