重积分的计算

一、二重积分与三重积分的定义

重积分有深刻的几何与物理背景，我们生活在一个三维空间，很多现象用一维的知识是难以解决的，故对重积分的背景问题必须稍有认识，二重积分的背景是如何计算曲顶柱体的体积；三重积分的背景可以是三维物体对其外部一点的引力等等。

重积分的定义完全类似于Riemann积分的定义：分割，取点并作和，求极限。

重积分的积分区域通常是平面或空间的有界闭区域，而被积函数往往是连续函数。可积性的讨论往往显得不甚重要，关键是如何计算。

详细的定义在此不再罗列。

二、重积分的计算之一—化为累次积分

1．设平面闭区域D为X－型区域：φ₁（x）≤y≤φ₂（x），a≤x≤b，则

2．设平面闭区域D为Y－型区域：φ₁（y）≤x≤φ₂（y），c≤y≤d，则

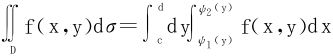
3．设Ω为空间的有界闭区域，其在xy平面上的投影为D，Ω是由定义在D上的两个连续曲面Z＝φ（x，y）和Z＝ψ（x，y）（φ（x，y）<ψ（x，y）），以及过D的边界竖起的垂直于xy平面的柱面所围成，则

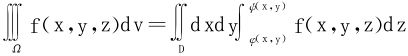
而对于右边的D上的二重积分，则可据第1、2条继续化为累次积分。如设

Ω＝｛（x，y，z）｜a≤x≤b，y₁（x）≤y≤y₂（x），z₁（x，y）≤z≤z₂（x，y）｝

则有

积分顺序是先写后积。

4．如果积分区域与某坐标轴相垂直的截面面积（这是关于这个坐标变量的函数）易求而被积函数又只含此坐标变量，那么此三重积分可化为二重积分再定积分计算。

设Ω＝｛（x，y，z）｜c≤z≤d，（x，y）∈D_z｝，则

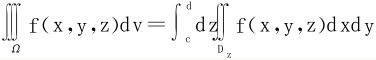
特别当f仅是z的函数时

式中｜D_z｜代表截面D_z的面积。

5．对称性的运用，当且仅当积分区域与被积函数都具有对称性时，才可用此性质。

几点说明：

1．有时同一区域既是X型又是Y型，则要合理地选取某种型号，对于三重积分，更具有选择余地。

2．有时积分区域既不是X型又不是Y型，则须将其进行恰当分割，成为若干个简单区域之并。

3．当被积函数是分“段”函数（即在不同区块内表达式不同）时，亦该将积分化为几个分区域积分之和。

4．当积分区域和被积函数都具有某种对称性时，可实现简化。

例1　计算下列重积分

（1）　D是以（0，0），（0，1），（1，1）为顶点的三角形区域；

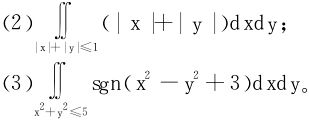
解　（1）D既是X－型又是Y－型区域，但视为X－型区域则积不出，必须视为Y－型区域

（2）利用对称性，

（3）分析，被积函数

又被积函数与积分区域都关于坐标轴对称，因此只要计算第一象限之部分。

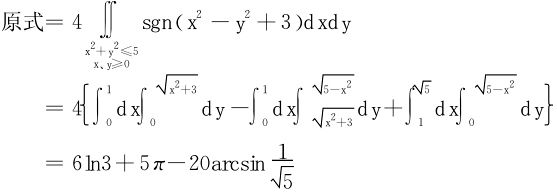
（双曲线y²－x²＝3与园周x²＋y²＝5在第一象限之交点为M（1，2）；涉及一重积分的计算内容非我们现在之重点，故不详细写出）

例2　设f（t）为连续函数，证明

证明　

例3　计算下述三重积分

（1）　Ω由曲面z＝xy，y＝x，x＝1，z＝0所围成；

（2），Ω是四面体：x，y，z≥0，x＋y＋z≤1；

（3）：Ω是椭球体之上半部分；

（4）　Ω是上小题中的整个椭球；

（5）　Ω是由曲面z＝xy和平面x＋y＋z＝1，及z＝0所围成；

（6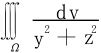）　Ω为棱台，六个顶点为A（0，0，1），B（0，1，1），C（1，1，1）；A₁（0，0，2），B₁（0，2，2），C₁（2，2，2）。

解　（1）Ω在xOy平面上的投影区域是

D＝｛（x，y）｜0≤x≤1，0≤y≤x｝

底面即为z＝0，顶面z＝xy

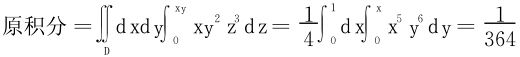
或解：先定出高度z＝z₀时，Ω的截面

依第四款化为先二重积分再定积分：

（3）高为z的平面去截积分区域，截面在平面上的投影D_z是一个椭园：

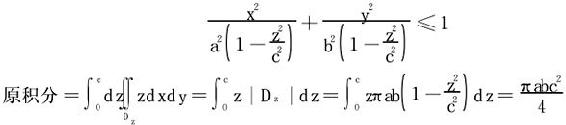
（4）依结构对称性，先算，方法如上，得出值为，由对称性知

注　（3）（4）两题用广义球坐标变换求解之法见后。

（5）由上述图形看出，积分区域的底在xy平面内，为三角形底面，顶由两部分构成，一部分平顶：z＝1－x－y（当（x，y）∈D₁时）；另一部分为曲顶：z＝xy（当（x，y）∈D₂时）。

图7-1

剩下的是定积分的计算，省略。

（6）作为棱台，其上底面即顶为大三角形A₂B₂C₂，下底面即为底三角形A₁B₁C₁。以高为z的平面去截，得截口区域D_z＝｛（x，y）｜0≤x≤y，0≤y≤z｝为Y型区域。

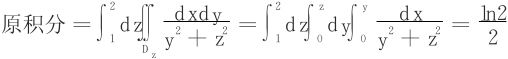
或解：视梯形A₁B₁B₂A₂为底，梯形A₁C₁C₂A₂为顶，则底区域为yz平面上的

D＝｛（y，z）｜0≤y≤z；1≤z≤2｝

顶面方程为x＝y，亦即积分区域可以写为

Ω＝｛（x，y，z）｜0≤x≤y，0≤y≤z，1≤z≤2｝

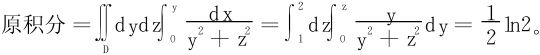
三、重积分计算之变量替换

1．二重积分的变量替换

特取极坐标变换x＝rcosθ，y＝rsinθ，就得

2．三重积分的变量替换

设有三维空间的变量代换

在与情形1完全类似的变换条件下，有

3．柱坐标变换

注　请大家思考柱坐标网的几何含义：r＝常数、θ＝常数、z＝常数各代表什么样的曲面，或了解柱坐标系中的“长方体”的几何形状。

4．球坐标变换

变量φ从z轴的正向起算（若从xy平面起算，则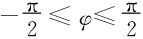，变换式要改）。

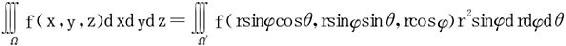
注　了解球坐标中“长方体”的含义（几何形态）。

5．广义球坐标变换

在广义球坐标下，三重积分的变量替换公式：

重积分变量替换的要点是：

i）使被积函数得到简化，或者积分区域变得易于定限；

ii）关键在于定出变换T的原象区域D′或Ω′；

iii）实际操作中，常常会先给出逆变换

而雅可比行列式计算遵从如下公式：

注　此式完全类似于一元反函数求导法，请阅§6.3末（18）式。

例4　选择适当变量替换计算下列各二重积分：

解　（1）作代换，则积分区域简化成uv平面中的矩形｝

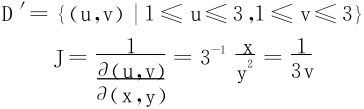
注　本题可直接从对称性分析得出结果是0（这叫做不算之算）！！由方程｜x｜＋｜y｜≤1表示的斜置方形区域皆可采用此变换化为标准方形区域。

（3）同（2）题变换，

通过代换，很难算的问题迎刃而解，请各位读者多多体会其中妙处。

（4）法一　令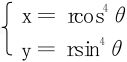

法二　令而另一个变换式如何选取呢？尝试用，则有

　　　

或行不行呢？此时，算得

D″＝｛（u，v）｜｜v｜≤u而0≤u≤1｝

思考　若令行不行呢？此时区域D′难求一些。读者不妨一试。

（5）区域关于y轴对称，故被积函数中关于x的奇次幂项的积分等于0。

于是原积分首先化简为

为了使被积函数和积分区域都得以简化，先令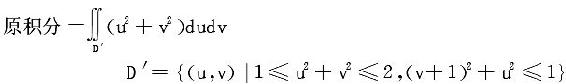

此积分区域完全在uv平面u轴的下方（见图7-2-（1）），由对称性

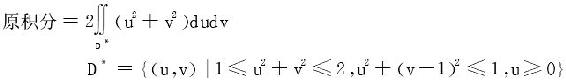
图7-2

（6）其实本题是广义二重积分。

被积函数有三个乘积因子，结合积分区域的特征易联想到应该令u＝x＋y，第二个变量如何令呢？

若令易想到，但x＝0时没有意义。不妨作为广义二重积分计算。此时，

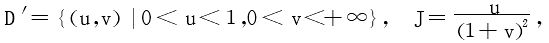
所以原积分变为

对三重积分的变量替换，基本要求是掌握常规的柱坐标变换和球坐标变换。

例5　求以下三重积分：

（1），Ω为椭球；

（2），Ω为椭园锥面：与平面z＝c所围成；

（3），Ω由z＝ay²，z＝by²，z＝αx，z＝βx，z＝h所围成的y>0的部分（h>0，0<a<b，0<α<β）；

（4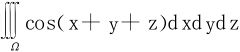），Ω为单位球体x²＋y²＋z²≤1。

解　（1）此题即为例3的第（3）小题。现在依据广义球坐标变换去解。

　　　，显得简洁明快。

（2）从积分区域分析，纯粹的球面坐标或广义球面坐标尚不能直接化简，故考虑先化为一个二重积分和一个一重积分之累次积分，再作二维变量替换。积分区域Ω在xOy平面的投影区域是D：

　　

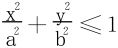
再利用二重积分的广义极坐标变换x＝arcosθ，y＝brsinθ

注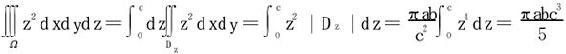　

其中D_z为高度为z的平面去截积分区域所得截口在xy平面的投影

其面积为。

（3）令，则Ω变成了

Ω′＝｛a≤u≤b，α≤v≤β，v≤w≤h｝

且求得，于是

（4）为简化被积函数，考虑变换使x＋y＋z＝0是新坐标系中uv坐标平面。亦即作一个坐标系的旋转，新坐标系中的三个坐标轴单位向量是

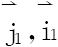取作x＋y＋z＝0的单位法向量，是平面x＋y＋z＝0内的两个正交单位向量，例如

这样得到的变量替换是一个正交变换，其表达式是

正交变换的雅可比行列式｜J｜＝1，单位球面仍变作单位球面。

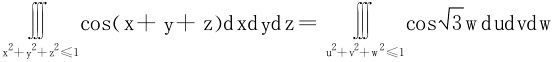
再利用柱面坐标u＝rcosθ，v＝rsinθ，w＝w，｜J｜＝r，积分区域就变成

Ω^*：0≤θ<2π，r²＋w²≤1

例6　利用重积分计算面积或体积

（1）曲线（x＋2y）²＋（2x＋3y）²＝8所围区域的面积S；

（2）曲面所围区域Ω的体积V。

解　（1）令u＝x＋2y，v＝2x＋3y，则D变为D′：u²＋v²≤8，且｜J｜＝1

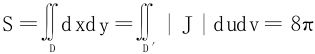
（2）令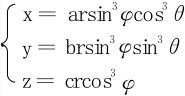　区域Ω变为Ω′：0≤r≤1，0≤φ≤π，0≤θ≤2π，

经较为繁琐的行列式计算得

或令x＝au³，y＝bv³，z＝cw³，先将Ω变换到Ω₁：u²＋v²＋w²≤1；

再对Ω₁使用球坐标变换。

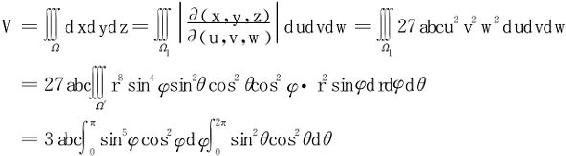
注　将复杂的变换分为两步较简单的或较熟悉的变换，可以极大地简化变换雅可比行列式的计算。

习题7.1

1．对下列累次积分，先换序再计算：

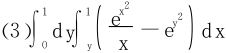
（浙江省高等数学竞赛2006年）

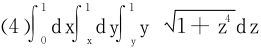
2．求累次积分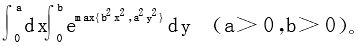

（浙江省高等数学竞赛2007年）

3．求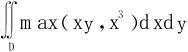，其中D＝｛（x，y）｜－1≤x≤1，0≤y≤1｝。

（浙江省高等数学竞赛2004年）

4．求积分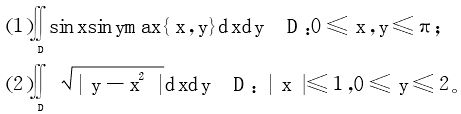

（北师大2002年）

5．求积分，其中f（u）为一元连续函数。

D：－1≤x≤1，x³≤y≤1。

6．求积分

7．计算下述各三重积分：

8．求，其中

Ω：－1≤x≤1，－1≤y≤1，－1≤z≤1。

（北师大2005年）

9．计算广义重积分。

（北师大2006年）

10．求曲面（x²＋y²）²＋z⁴＝y围成的立体体积。

11．求曲面和三个坐标平面围成的在第一卦限部分区域的体积。

12．设f在正方形区域［0，1；0，1］上连续，在（0，0）处可微，f（0，0）＝0。求极限

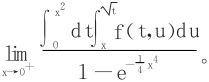
13．设函数f在［0，＋∞）上连续，且满足方程

求f（t）

（1997年数学（三））

14．设f（t）为连续函数，t≥0。并且

求f（t）。

15．设f（u）为连续函数，Ω为x²＋y²＋z²≤1，证明

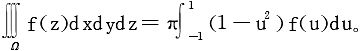
16．设f（u）连续，f（1）＝1，定义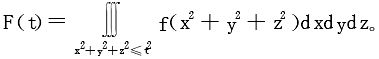

证明：F′（1）＝4π。

（华东师大98年）

17．设f（x₁，x₂，…，x_n）为n维方形域0≤x_i≤1（i＝1，2，…，n）内的连续函数。证明

18．设f（u）为连续函数，证明

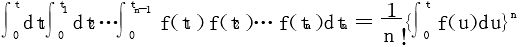
19．设f（u）∈C（R），n∈N，n维区域D：0<x₁<x₂<…<x_n<1，证明：

（北京师范大学2001年）

以下三题可以采用n维空间的球面坐标变换。

x₁＝rcosφ₁，

x₂＝rsinφ1cosφ₂，

……

x_n－1＝rsinφ₁sinφ₂…sinφ_n－2cosφ_n－1，

x_n＝rsinφ₁sinφ₂…sinφ_n－2sinφ_n－1。

变换的雅可比行列式是

J＝r^n－1sin^n－2φ1sin^n－3φ₂…sinφ_n－2。

20．计算

21．设f（u）为连续函数，化n重积分

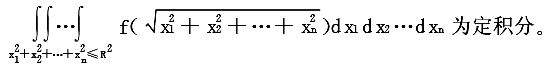
22．求n维球体的体积。