§7.3 第二型曲线积分
一、第二型曲线积分的概念
第二型曲线积分又称对坐标的曲线积分,其物理原型是变力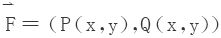 沿着有向曲线C从一端A至另一端B时所作的功。
沿着有向曲线C从一端A至另一端B时所作的功。
回忆变力(大小变化而方向不变)F(x)沿直线所作的功可用定积分表示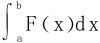 。
。
若力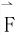 方向和物体运动方向成一个角度θ,则当物体从起点A(a)运动到终点B(b)时,力
方向和物体运动方向成一个角度θ,则当物体从起点A(a)运动到终点B(b)时,力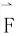 所作的功是
所作的功是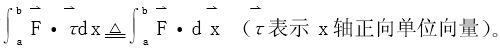
现在假设力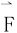 不仅大小变化,方向也变化,并且物体运动也变为沿有向曲线C的曲线运动时,用上述一元思路就不行啦。
不仅大小变化,方向也变化,并且物体运动也变为沿有向曲线C的曲线运动时,用上述一元思路就不行啦。
设平面力场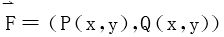 沿平面有向曲线C从A端至B端,求所做的功。将有向线段C分割,分点依次为
沿平面有向曲线C从A端至B端,求所做的功。将有向线段C分割,分点依次为
A=A0,A1,A2,…,An=B,
记Ak=(xk,yk)
Δxk=xk-xk-1,Δyk=yk-yk-1
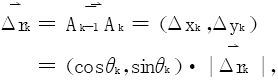
Δsk表示小弧段Ak-1Ak之弧长。
θk为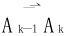 跟x轴正向的夹角,在分割相当细密时(
跟x轴正向的夹角,在分割相当细密时(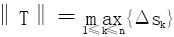
 充分小),变力
充分小),变力 在弧段Ak-1Ak上便可近似看作常力
在弧段Ak-1Ak上便可近似看作常力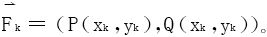
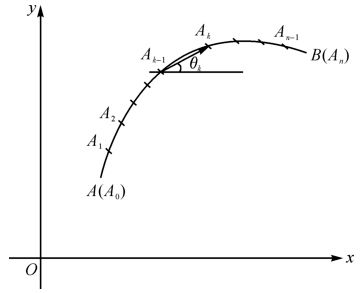
图7-3
而弧段Ak-1Ak近似于有向线段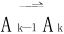 ,常力
,常力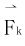 沿有向线段
沿有向线段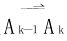 所作的功是
所作的功是
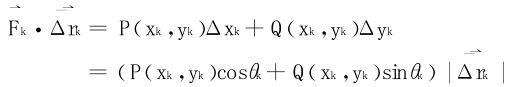
当‖T‖→0时,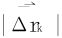 可以用Δsk代替。最后得出功
可以用Δsk代替。最后得出功
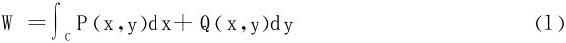
或写成 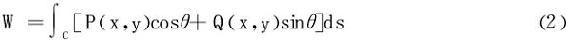
式中θ=θ(x,y)是曲线C在点M(x,y)处的与曲线走向一致的切向量跟x轴正向夹角,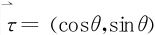 则是单位切向量。
则是单位切向量。
为了便于向高维推广,记切向量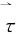 跟x轴正向、y轴正向所成的角分别是α,β。
跟x轴正向、y轴正向所成的角分别是α,β。
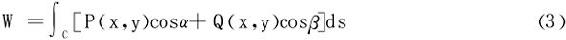
若记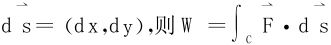 就是第二型曲线积分。
就是第二型曲线积分。
用微元法分析,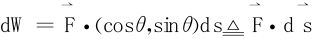 会更直观一些。思想方法上,仍然是分割、作和、求极限三步曲。
会更直观一些。思想方法上,仍然是分割、作和、求极限三步曲。
注 (2)式定义的第二型曲线积分形式上是用第一型曲线积分转化的。三维空间的第二型曲线积分定义类似于二维,简述于下。定义式:
α,β,γ是有向曲线C在点(x,y,z)处与曲线方向一致的切向量跟x,y,z轴正向的夹角。(cosα,cosβ,cosγ)是曲线的单位切向量,记为 。
。
此即三维力场 沿有向曲线C所做的功:
沿有向曲线C所做的功:
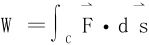
二、第二型曲线积分的计算
1.平面曲线
若f(x,y)是定义在光滑的平面有向曲线C:x=x(t),y=y(t),t从α到β上的连续函数,则
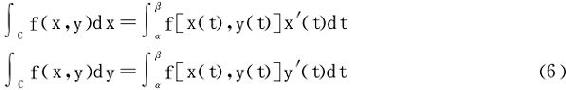
这是C的方向相应于参数t从α变到β。即t=α对应曲线C的起点,t=β对应曲线C的终点。特别注意,α可以大于β。
2.空间曲线
3.格林公式
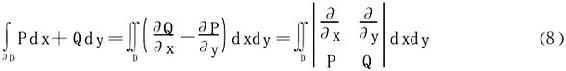
特别需要指出的是,D的边界曲线取的方向为正向,而正向依左侧原则确定:当沿着该方向前进时,区域D总在左侧。对于有洞的复连通区域,必须特别留意曲线的走向。特地以P(x,y)=-y,Q(x,y)=x,得出由封闭曲线C围成的平面区域求面积公式:
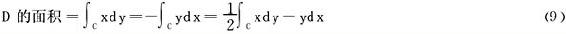
C相对于区域D取正向。对于以参数形式给出的闭曲线,上式较为方便适用。
4.Stokes公式
设光滑曲面∑的边界C是按段光滑的连续曲线,若函数P,Q,R在∑上一阶连续可偏导,则
引入向量场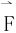 的旋度
的旋度
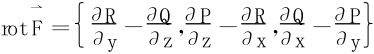
 为边界线的单位切向量
为边界线的单位切向量 为曲面∑指定一侧的单位法向量,则Stokes公式便可写为
为曲面∑指定一侧的单位法向量,则Stokes公式便可写为
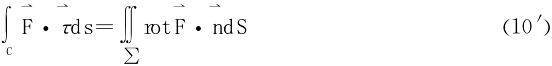
例1 计算下述各曲线积分
(1)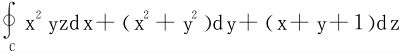
C:x2+y2+z2=5与z=x2+y2+1的交线,从z轴正向看C为顺时针方向;
(2)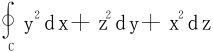
C:x2+y2+z2=a2,x2+y2=ax(z≥0,a>0)的交线,从x轴正向看去,C逆时针;
(3)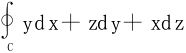
C:x2+y2+z2=a2,x+y+z=0,从x轴正向看去,按逆时针方向。
解 (1)曲线C的方程可以转化为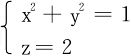
参数方程为x=cost,y=sint,z=2
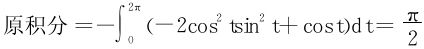
(2)引入柱坐标,曲线可表示为x=acos2θ,y=acosθsinθ,z=a|sinθ|,θ从 变至
变至 时,方向与曲线的方向一致,代入算得:
时,方向与曲线的方向一致,代入算得:
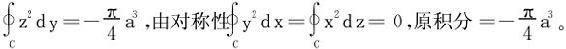
(3)法一 在第2小节的例2中,已经建立起圆周C的参数方程,原则上代入公式(7)即可算得,但计算量相对偏大,有待改进。
曲线C的方程组消去z得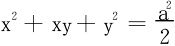 ,配方得
,配方得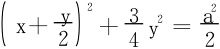
令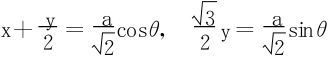 得
得
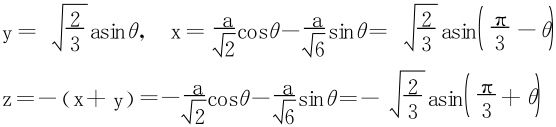
当θ从0到2π时,曲线c是否依题设的正向走?可考虑几个特殊点如
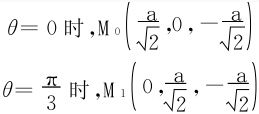
应该可以看出θ增加的方向跟C的正向一致。于是
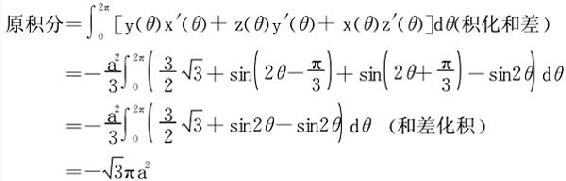
法二 以Stokes公式解。平面x+y+z=0截球x2+y2+z2≤a2的截面为∑,取外侧。依Stokes公式和对称性
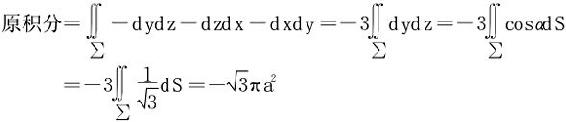
第二种解法比起第一种解法来真有四两拔千斤之奇效!
例2 计算下列各第二型曲线积分:
(1)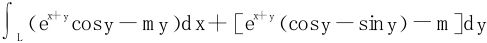 ,
,
L:圆周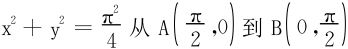 的圆周弧段;
的圆周弧段;
(2)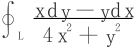 ,L是点(1,0)为中心、R(R>0,R≠1)为半径的圆周逆时针方向;
,L是点(1,0)为中心、R(R>0,R≠1)为半径的圆周逆时针方向;
(3)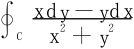 ,闭曲线C不过原点且取逆时针方向。
,闭曲线C不过原点且取逆时针方向。
解 (1)设OABO所围的四分之一圆域为D,依格林公式
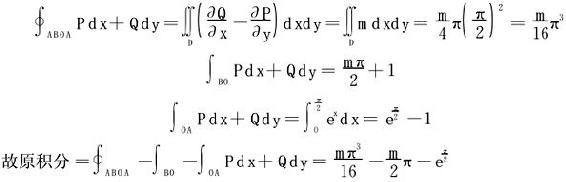
(2)易知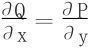 (当(x,y)≠(0,0)时)
(当(x,y)≠(0,0)时)
当R<1时,由Green公式知原积分=0;
当R>1时,取ε>0,使椭圆L′:x=εcost,y=2εsint,0≤t≤2π。
位于圆周L的内部,取L′的方向为逆时针,于是
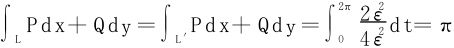
于是
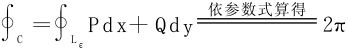
注 通过本例可以看出,格林公式的最大效用在于将复杂的甚至是抽象的积分曲线转化为简单的,具体的积分曲线,从而简化了计算。对此须多加运用和体会。
例3 计算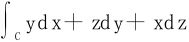 ,其中C是从点A(a,0,0)沿以下曲线到B(0,0,c)。
,其中C是从点A(a,0,0)沿以下曲线到B(0,0,c)。
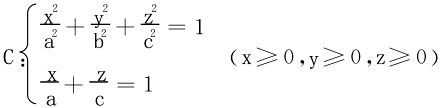
解一 用曲线的参数方程解,从曲线C的联立方程消去z得
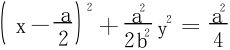
于是令 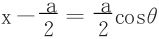 ,
,
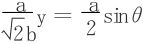
代入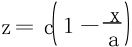 得:
得:
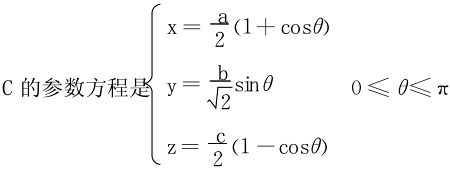
将C的起点A(a,0,0)、终点B(0,0,c)坐标代入核实参变量θ的范围是0≤θ≤π,且A点对应θ=0。
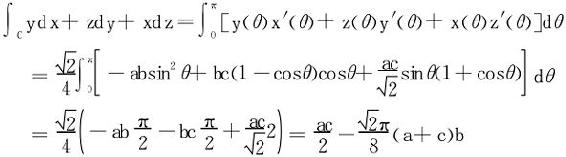
解二 用Stokes公式
首先将曲线段C补充成闭合曲线, 记为L,以此L为边界的曲面不止一个,在使用Stokes公式时,应选择最简的曲面(一般如平面块较妥),如图7-4。
记为L,以此L为边界的曲面不止一个,在使用Stokes公式时,应选择最简的曲面(一般如平面块较妥),如图7-4。
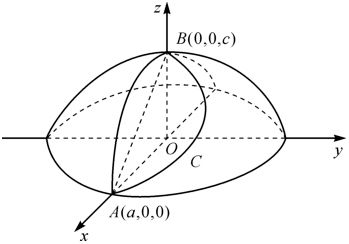
图7-4
L既在平面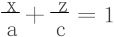 上,此为显式平面
上,此为显式平面
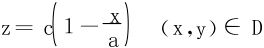
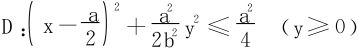
取平面的上侧,由Stokes公式
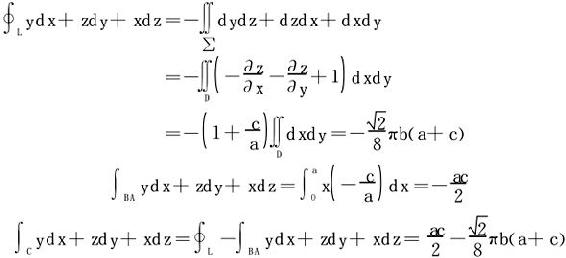
三、曲线积分与路径无关的充要条件·保守场·原函数
1.何谓保守场
若向量场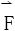 沿任何按段光滑曲线的第二型曲线积分,只与曲线的起点和终点有关,而与曲线的形状无关,则称
沿任何按段光滑曲线的第二型曲线积分,只与曲线的起点和终点有关,而与曲线的形状无关,则称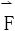 为保守场。
为保守场。
2.保守场的充要条件
(1)向量场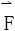 为保守场的充要条件是:沿任何无重点的,按段光滑的闭曲线C有
为保守场的充要条件是:沿任何无重点的,按段光滑的闭曲线C有
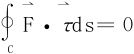
(注:二维向量场,三维向量场可以分开写)
(2)设D⊂R2是单连通闭区域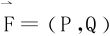 ,若P,Q都在D内有连续的一阶偏导数,则
,若P,Q都在D内有连续的一阶偏导数,则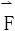 是保守场的充要条件是
是保守场的充要条件是
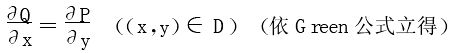
(3)设G为空间中按曲面单连通的区域,则G上的向量场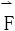 是保守场的充要条件是在G上
是保守场的充要条件是在G上
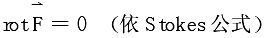
3.原函数
(1)先以二元函数为例。设二元函数u(x,y)二阶连续可偏导,则
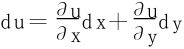
记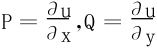 ,当u(x,y)二阶连续可偏导时,一定有
,当u(x,y)二阶连续可偏导时,一定有
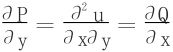
此说明(P,Q)满足保守场条件。
反之,若已知(P,Q)是保守,则Pdx+Qdy是一个全微分式,即存在一个二元函数u(x,y),使得

成立。
如何求解二元的原函数u(x,y)呢?
对保守力场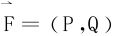 而言,第二型积分与路径无关,在单连通区域D内选择一定点A(x0,y0)作为起点,动点B(x,y)作为终点,考虑变上限曲线积分:
而言,第二型积分与路径无关,在单连通区域D内选择一定点A(x0,y0)作为起点,动点B(x,y)作为终点,考虑变上限曲线积分:
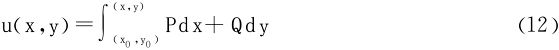
u(x,y)除去积分常数外是唯一确定的,且满足du=Pdx+Qdy,仍称u(x,y)为(全)微分式Pdx+Qdy的一个原函数,也叫做向量场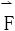 的力函数,-u(x,y)≜φ(x,y)叫做场
的力函数,-u(x,y)≜φ(x,y)叫做场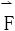 的位函数,保守场
的位函数,保守场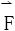 一定是位场,且有
一定是位场,且有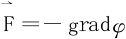 。此处grad表示梯度。
。此处grad表示梯度。
在具体用(12)式求解原函数时,积分路径可选择平行于坐标轴的折线段:
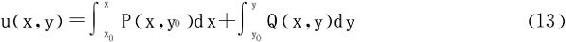
或
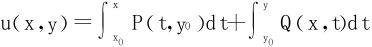
(2)若三维向量场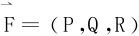 是保守场,在单连通区域G内,P,Q,R都有一阶连续偏导数,则Pdx+Qdy+Rdz是某一函数u(x,y,z)的全微分,且
是保守场,在单连通区域G内,P,Q,R都有一阶连续偏导数,则Pdx+Qdy+Rdz是某一函数u(x,y,z)的全微分,且
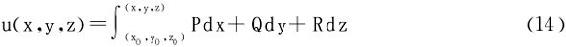
u(x,y,z)也叫做(全)微分式Pdx+Qdy+Rdz的原函数。
如何确定积分路径?
如果坐标原点(0,0,0)在G内部,则起始点可以取作原点0,积分路径仍沿用平行于坐标轴的折线段从(x0,y0,z0)到达(x,y,z)。
可以自行写出类似于(12)式的化为一元定积分形式的原函数公式。
注 (12),(14)式的地位相当于微积分学基本定理,若已求得微分式(二维、三维)的原函数u,则以A起点B终点的曲线积分(跟具体路径无关)
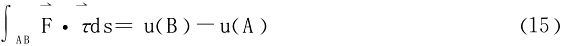
此式类似于牛顿-莱布尼兹公式。
例4 找出函数f>0,满足:
(1)f连续可微且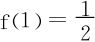
(2)在右半平面内沿任一分段光滑封闭曲线L的积分有
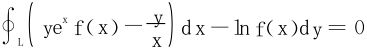
解 由积分跟路径无关的充要条件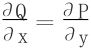 知,∀x>0,有
知,∀x>0,有
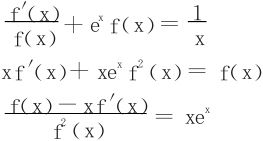
即
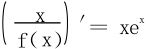
所以
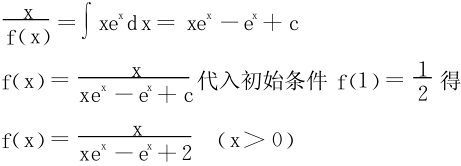
例5 (1)设du=ex-y[(1+x+y)dx+(1-x-y)dy],求原函数u;
(2)求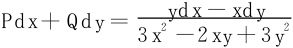 的原函数;
的原函数;
(3)判定向量场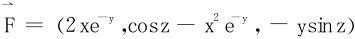 是否保守场;若是,求其原函数。(也叫做力函数)。
是否保守场;若是,求其原函数。(也叫做力函数)。
解 (1)P(x,y)=ex-y(1+x+y),Q(x,y)=ex-y(1-x-y)在全平面上连续可偏导,
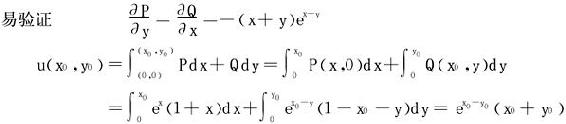
故原函数为u(x,y)=ex-y(x+y)+c (c为任意常数)。
(简化记号:也可以先求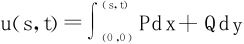 )
)
(2)分母3x2-2xy+3y2的判别式<0,故y>0时,分母恒正,不难验证
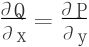
故在区域y>0上,积分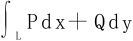 与路径无关。
与路径无关。
取起始点M0(0,1),沿路径M0(0,1)→M1(0,y)→M(x,y),则得一个原函数是:
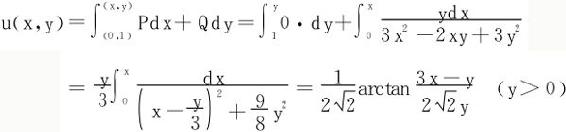
(3)依Stokes公式,积分与路径无关之充要条件是
代入验算易知 是保守场。
是保守场。
取折线路径进行变限积分(0,0,0)→(x,0,0)→(x,y,0)→(x,y,z)
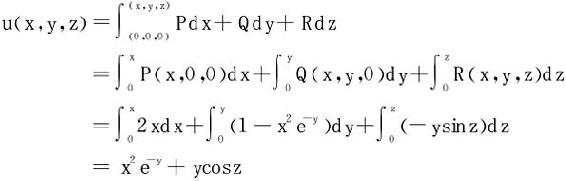
习题7.3
1.设P(x,y)具有一阶连续偏导数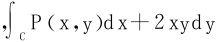 与路径无关,且
与路径无关,且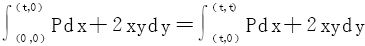 ,求P(x,y)。
,求P(x,y)。
2.设x>-1时,函数f(x)连续可微,且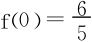 ;在半平面x>-1的任意闭曲线C上恒有
;在半平面x>-1的任意闭曲线C上恒有 ,试求出f(x),并计算曲线积分
,试求出f(x),并计算曲线积分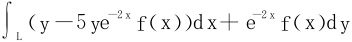 ,其中L以A(1,0)起始至B(2,3)终止。
,其中L以A(1,0)起始至B(2,3)终止。
3.求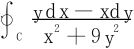 ,C:x2+(y-1)2=9,取逆时针方向。
,C:x2+(y-1)2=9,取逆时针方向。
4.设f在R内连续可导,求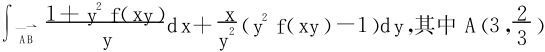 ,B(1,2)。
,B(1,2)。
5.假定闭曲线C:x2+y2+z2=1,y=z,其方向与z轴正向构成右手螺旋系,计算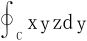 。
。
6.求积分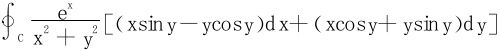 ,其中C为不自交的包含原点在其内部的光滑闭曲线。
,其中C为不自交的包含原点在其内部的光滑闭曲线。
(提示: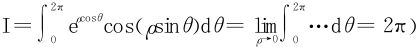
7.设P(x,y),Q(x,y)除(0,0)外连续,且有连续的偏导数,且(x,y)≠(0,0)时,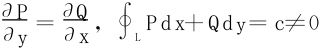 ,L为逆时针向的单位圆。试证明:存在连续可微函数F(x,y),使得(x,y)≠(0,0)时
,L为逆时针向的单位圆。试证明:存在连续可微函数F(x,y),使得(x,y)≠(0,0)时
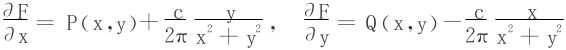
8.设函数f(u)具有一阶连续导数,证明对任何光滑闭曲线L有
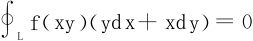
9.设函数f(u)连续,证明对任何逐段光滑封闭曲线L有
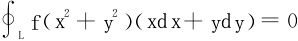
10.求所有有连续偏导数的函数P(x,y)和Q(x,y),使得线积分
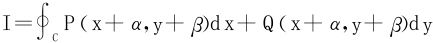
对于任何封闭的曲线C以及常数α,β保持不变(即与常数α,β无关)
11.计算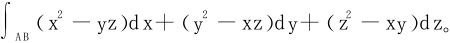
AB为螺线x=cosθ,y=sinθ,z=θ由A(1,0,0)到B(1,0,2π)的一段。
12.求解方程(3y+4xy2)dx+(2x+3x2y)dy=0。
13.设C为光滑封闭曲线,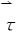 为跟C的正向一致的单位切向量,证明
为跟C的正向一致的单位切向量,证明
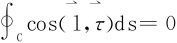
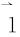 为一个固定的常向量。
为一个固定的常向量。
14.设u=u(x,y)有二阶连续偏导数,试证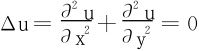 的充要条件是
的充要条件是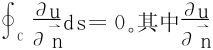 为沿外法线方向的方向导数。
为沿外法线方向的方向导数。
15.设D是由平面光滑闭曲线C所围成的平面区域,u(x,y),v(x,y)在D内二阶连续可偏导,求证:
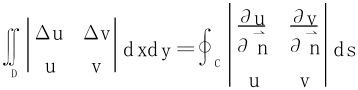
其中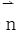 为外法线单位向量,C取正向。
为外法线单位向量,C取正向。
16.计算高斯积分
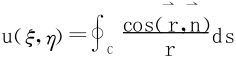
这里C是无重点光滑闭曲线,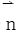 是曲线C在点(x,y)处外法向量,
是曲线C在点(x,y)处外法向量,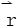 为连接点(ξ,η)和点(x,y)的矢径,
为连接点(ξ,η)和点(x,y)的矢径,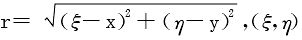 不在C上。
不在C上。
第7题解:注意到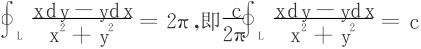 ,于是
,于是
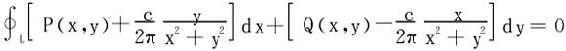
由条件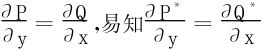 (P*,Q*代表上式中新函数)
(P*,Q*代表上式中新函数)
故沿着任何封闭光滑曲线一定有
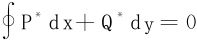
从而存在一个函数F(x,y)使得
dF=P*dx+Q*dy
于是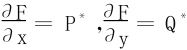 ,即得所欲证明。
,即得所欲证明。
(换言之,任取一点(x0,y0)≠(0,0),对其他任一点(x,y),作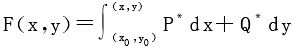 ,此F满足要求)。
,此F满足要求)。
第9题解:令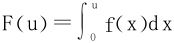 是f(u)的原函数,
是f(u)的原函数,
则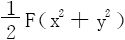 是f(x2+y2)(xdx+ydy)的原函数,从而
是f(x2+y2)(xdx+ydy)的原函数,从而
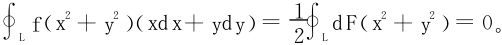
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














