一、广义积分的收敛性概念
1.有界函数在无穷区间上的广义积分
设∀A>a,f(x)在[a,A]上可积,称

为无穷限广义积分。
(1)式右边的极限存在时,称广义积分 收敛;否则就说广义积分
收敛;否则就说广义积分 发散。
发散。
类似定义广义积分 的收敛性。
的收敛性。
若广义积分 都收敛,称广义积分
都收敛,称广义积分 收敛。
收敛。
2.无界函数在有限区间上的广义积分(瑕积分)
注 瑕积分和Riemann积分在记号上没有任何区别,要靠判断被积函数是否有界才能明确是哪一类积分。
3.混合型广义积分
设函数f(x)在x=a的邻近无界, ,但∀η>0,∀A>a+η,f(x)在[a+η,A]上可积。若
,但∀η>0,∀A>a+η,f(x)在[a+η,A]上可积。若 存在,称广义积分
存在,称广义积分 收敛当且仅当瑕积分
收敛当且仅当瑕积分 同时收敛。(a<b)
同时收敛。(a<b)
4.绝对收敛、条件收敛
(3)瑕积分 的绝对收敛、条件收敛类似定义。
的绝对收敛、条件收敛类似定义。
二、广义积分收敛性的判别法
对于定积分,积分值的计算是核心任务。而对于广义积分,积分值的计算往往较困难。在大多数情况下只能退而求其次判断其收敛性。当然广义积分值的计算亦是一个重要内容,需要许多非常规技巧甚至需要含参变量积分的相关知识。这些我们将在稍后(本章第4节)介绍。现在重点讨论广义积分收敛性的判别。主要以无穷积分为例。
1.柯西准则
 收敛的充要条件是:
收敛的充要条件是:
∀ε>0,∃G>a,st∀A′,A″>G,恒有 。
。
2.绝对收敛
若 收敛,则
收敛,则 必收敛
必收敛
对于非负的被积函数,有以下3~6条判别法则:
3.比较判别法
(1)若0≤f(x)≤g(x)且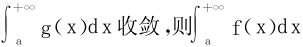 收敛;
收敛;
(2)若f(x)≥g(x)≥0且 发散。
发散。
4.比较判别法的极限形式
设f(x)非负,g(x)恒正,且 ,则
,则
(1)若0≤λ<+∞,且 ;
;
(2)若0<λ≤+∞,且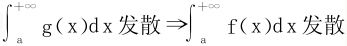 。
。
5.无穷积分的指数判别法
设 ,
,
(1)若p>1, ;
;
(2)若p≤1, 。
。
6.瑕积分的指数判别法
(1)若 ;
;
(2)若 。
。
7.Abel判别法和Dirichlet判别法
Abel判别法: 收敛,
收敛, ;
;
Dirichlet判别法:∀A>a, 关于A有界,当x→+∞时g(x)单调趋于
关于A有界,当x→+∞时g(x)单调趋于 。
。
8.与数项级数收敛性的转化
(1)设函数f(x)在[1,+∞)上非负递减,则无穷积分 同敛散;
同敛散;
(2)设f(x)在[1,+∞)上非负,则无穷积分 同敛散;
同敛散;
对于一般的函数(没有非负的条件),上述结论未必成立。如取f(x)=sin2πx。
尽管如此,对于一般的函数我们有以下的无穷积分和数项级数收敛性的转化结果:
(3)无穷积分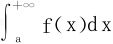 收敛的充要条件是:对任一列An↗+∞,A1=a,数项级数
收敛的充要条件是:对任一列An↗+∞,A1=a,数项级数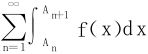 皆收敛。
皆收敛。
证明 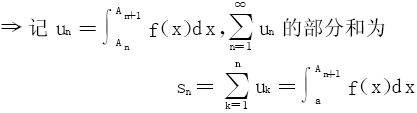
易知  。
。
记 存在当且仅当对任一列An↗+∞,
存在当且仅当对任一列An↗+∞,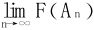 存在。而F(An+1)=sn为级数
存在。而F(An+1)=sn为级数 前n项部分和。
前n项部分和。
例1 判断下列各积分的敛散性:。

解 (1)当p>1时积分绝对收敛;当0<p≤1时,利用Dirichlet判别法知收敛,又因为 而
而 发散,
发散, 收敛,得知0<p≤1时
收敛,得知0<p≤1时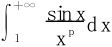 条件收敛。
条件收敛。
(2)利用阿贝尔判别法及第(1)小题结论知收敛。
思考 绝对收敛性和条件收敛性如何?
(3)x=0可能是奇点,因为
所以p<3时 收敛。
收敛。
对于x=+∞处,p>1时,取λ,st1<λ<p,
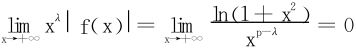 ,得p>1时
,得p>1时 收敛。
收敛。
当p≤1时,取λ,stp≤λ≤1,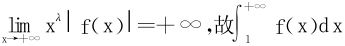 发散。
发散。
所以1<p<3时,积分 收敛。
收敛。
(4)因为 发散。
发散。
例2 判断下列各瑕积分的敛散性。

解 (1) ,瑕积分收敛。
,瑕积分收敛。
(2)因为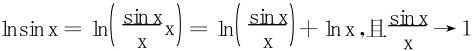 (x→0),
(x→0),
所以原积分的敛散性等价于 的敛散性,
的敛散性,
又 因为 收敛。
收敛。
或直接求极限 可得相同结果。
可得相同结果。
(3) ,所以积分发散。
,所以积分发散。
例3 设f(x)>0,且单调下降,试证 同敛散。
同敛散。
证明 先设 收敛,由比较判别法易知
收敛,由比较判别法易知 收敛;反之,若
收敛;反之,若 收敛,因
收敛,因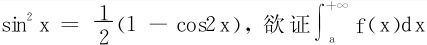 收敛,只需证
收敛,只需证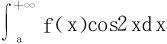 收敛。
收敛。
由于f(x)>0,且单调下降,故 存在。若A>0,则由Cauchy准则易知
存在。若A>0,则由Cauchy准则易知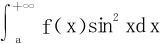 发散。于是
发散。于是 ,由狄利克雷法则,
,由狄利克雷法则, 收敛。从而
收敛。从而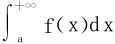 收敛。
收敛。
例4 讨论如下积分的敛散性(p>0):
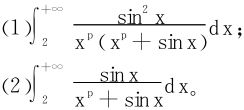
解 (1)比较判别法。
易知
若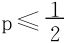 ,由积分
,由积分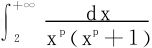 发散,结合例3结论知原积分为发散。
发散,结合例3结论知原积分为发散。
(2)利用(1)的结果及等式 ,当且仅当
,当且仅当 时积分收敛。
时积分收敛。
例5 讨论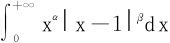 的敛散性。
的敛散性。
解 x=0,1是可能的奇点,
对于x=0,f(x)~xα,故α>-1时, 收敛;
收敛;
对于x=1,f(x)~|x-1|β(x→1),故β>-1时, 都收敛;
都收敛;
对于+∞处,f(x)~xα+β(x→+∞),故α+β<-1时, 收敛。
收敛。
综合起来,当α>-1,β>-1,α+β<-1时,原积分收敛。
习题8.1
1.讨论下述广义积分的敛散性:

2.判断下述广义积分的敛散性:
3.判断下列广义积分的收敛性和绝对收敛性:

4.证明 。
。
5.证明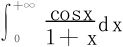 收敛且其绝对值不大于1。
收敛且其绝对值不大于1。
6.若f(x)在[0,+∞)上一致连续, 。
。
7.设f(x)在[0,+∞)上单调下降,且 。
。
8.设xf(x)在[0,+∞)上单调下降,且 。
。
9.设f(x)在[0,+∞)上可导,且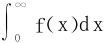 收敛,则∃{xn}↗+∞,
收敛,则∃{xn}↗+∞,
10.设f(x)在[a,+∞)上可导,当x→+∞时,f′(x)↗+∞,则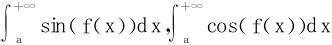 都收敛。
都收敛。
11.设f(x)在任何有限区间[0,a](a>0)上正常可积,于[0,+∞)上绝对可积,则

12.设f(x)在[0,+∞)上连续可微,且 ,f′(x)≤C。试证
,f′(x)≤C。试证 。
。
13.讨论积分 (α>0,β>0)的敛散性。
(α>0,β>0)的敛散性。
(注 此题是本节例1(4)的推广,可参阅[11]第八章)
14.设f(x)在[0,+∞)上连续,广义积分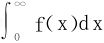 绝对收敛,试证。
绝对收敛,试证。
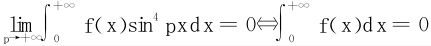
(浙江大学1998年)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















