功能原理与机械能守恒定律

由质点系的动能原理

内力中既有保守力，也有非保守力，因此内力做的功可以分为保守内力做的功和非保守内力做的功两部分．即

由式（2.16），保守力的功等于相应势能增量的负值，所以

代入上式得

系统的动能和势能之和叫做系统的机械能，用E表示，即，若用E1、E2分别表示系统初态和末态时的机械能，则

上式表明，外力和非保守内力做功的总和等于系统机械能的增量．这一结论就是质点系的功能原理．

功能原理全面概括和体现了力学中的功能关系，它涵盖了力学中所有类型力的功以及所有类型的能量，质点和质点系的动能定理只是它的特殊情形，功能原理是普遍的功与能的关系．由于动能定理的基础是牛顿运动定律，故功能原理也只适用于惯性系．

或　　

这就是说，当外力和非保守内力都不做功或所做的总功为零时，系统内各质点动能和势能可以相互转换，但系统的机械能保持不变，这就是机械能守恒定律．

在机械运动范围内，所涉及的能量只有动能和势能．由于物质运动形式的多样性，我们还将遇到其他形式的能量，如热能、电能、原子能等．如果系统内有非保守力做功，则系统的机械能必将发生变化．但在机械能增加或减少的同时，必然有等值的其他形式能量在减少和增加．考虑到诸如此类的现象，人们从大量的事实中总结出了更为普遍的能量守恒定律，即：对于一个不受外界作用的孤立系统，能量可以由一种形式转变为另一种形式，但系统的总能量保持不变．

例2.6　如图2.11所示，一雪橇从高度为50m的山顶上A点沿冰道由静止下滑，山顶到山下的坡道长500m，雪橇滑至山下B点后，又沿水平冰道继续滑行，滑行若干米后停止于C处．若雪橇与冰道的摩擦系数为0.05，求雪橇沿水平冰道滑行的路程．设点B处可视为连续弯曲的滑道，并略去空气阻力．

图2.11　例2.6图

解　把雪橇、冰道和地球作为一个系统，作用于雪橇上的力为：重力P、支持力N、摩擦力f，其中重力是保守力，只有非保守内力——摩擦力做功．由功能原理，雪橇在滑行过程中，摩擦力做的功为

式中A1和A2分别为雪橇沿斜面下滑和沿水平冰道滑行时，摩擦力所做的功．EP1和Ek1为雪橇在山顶A点时的势能和动能，EP2和Ek2为雪橇静止在水平滑道C点时的势能和动能．取水平滑道处的势能为零，由题意知，EP1=mgh，Ek1=0，EP2=0，Ek2=0

由功的定义

因斜坡坡度很小，

而

所以

代入数据求得

本题也可以用牛顿第二定律求解，但运算要复杂得多．

解　以地球和物体组成的系统为研究对象，物体从地面出发飞离时，因忽略其他阻力，只有保守内力做功，所以这一系统的机械能守恒．设距地球无穷远处为引力势能零点，则物体在地面所具有的势能为

以地面为参考系，设物体离开地面时的速度为v，远离地球时的速度用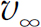表示，由机械能守恒定律

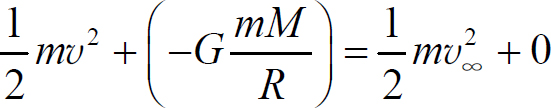
当远离地球时的速度时，对应最小逃逸速度

由于地球表面引力

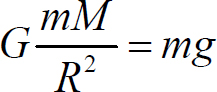
所以

以上计算出的最小逃逸速度又叫做第二宇宙速度．第一宇宙速度是物体可以环绕地球运行所需的最小速度，可以用牛顿第二定律求得，其值为．第三宇宙速度则是使物体脱离太阳系所需的最小发射速度（计算过程较为复杂），其数值为．