配位化合物的晶体场理论（阅读）

皮塞（Bethe）在1929年首先对处在晶体中的金属离子作了量子力学的处理而提出晶体场理论（crystal field theory，缩写为CFT）。但直到20世纪50年代初，人们发现用晶体场理论能很好地解释过渡金属配合物的光谱以后，它才作为配合物的化学键理论开始得到应用。

（一）晶体场理论的基本要点

1.中心原子（金属阳离子）和配体（阴离子或极性分子）之间通过静电作用结合形成配合物。

2.配体形成的负电场（称晶体场）对金属离子产生静电引力的同时，还会对金属离子的d轨道产生斥力，使原来简并的5个d轨道的能量不再相同，即发生能级分裂。分裂的方式取决于晶体场的对称性。

3.由于金属离子d轨道的能级分裂，电子优先填充在能级较低的轨道上，一般会引起配合物的总能量比d轨道未分裂时降低，从而增加配合物的稳定性。

晶体场理论是一种静电理论，它把配合物中中心原子与配体的相互作用看作类似于离子晶体中阴阳离子间的相互作用。这种相互作用只是静电吸引和排斥，不形成共价键。虽然模型简单，却可得出一些有意义的结果。下面主要讨论在配体负电场中过渡金属离子d轨道的能级分裂及其对配合物性质的影响。

（二）中心原子d轨道的能级分裂

1.八面体场中的能级分裂

先假设金属离子处于一个球壳内的中心，球壳上均匀分布着6个配体的总电荷，金属离子的5个d轨道受到球壳上负电荷的斥力完全均等，故能量比原来自由离子的d轨道高，但并不发生能级分裂，将这种静电场称为球形场。但在八面体配合物中，6个配体分别处于八面体的6个顶点，形成的静电场是非球形对称的，称为八面体场。八面体场中金属离子的5个d轨道受到的斥力是不均等的。可在直角坐标中表示配体与金属离子5个d轨道的相对空间关系，如图3-5所示（设金属离子处于坐标的原点）。

图3-5 八面体场中6个配体（以●表示）与金属离子5个d轨道的相对空间关系

可见，沿坐标轴方向伸展的d_x2—y2和d_z2轨道正好与配体相“撞”，受到配体电场的强烈排斥而能量升高较多。由于两者在八面体场中实际上是等价的，所以d_x2—y2和d_z2轨道具有相同的能量，形成一组二重简并的轨道，晶体场理论以dγ表示。夹在坐标轴之间的d_xy、d_xz和d_yz轨道受到的排斥较小，能量升高较少。由于三者对于配体有相同的空间分布，故能量相同，形成一组三重简并的轨道，晶体场理论以dε表示。这样金属离子原来简并的5个d轨道在八面体场中分裂成二组轨道，如图3-6所示。

图3-6 d轨道在八面体场中的能级分裂

需要强调的是，因配体静电场的影响，配合物中金属离子的5个d轨道的能级相对于自由金属离子都是升高的，只是有的升高较多（如上述d_x2—y2和d_z2），而有的升高较少（如上述d_xy、d_xz和d_yz）；引入球形场的概念主要是为了便于讨论和简化有关计算，实际上球形场中d轨道的能级就是配合物中5个分裂的d轨道能级的平均值。

2.四面体场中的能级分裂

若金属离子处于带有4个配体总电荷的球形场中，原来自由离子的5个d轨道能量也会升高，不发生能级分裂。但四面体场也是非球形对称的。将中心原子置于立方体的中心，直角坐标系的x、y、z轴分别指向立方体的面心，4个配体分别处于立方体8个顶点中相互错开的4个顶点位置，这样就构成了四面体场，如图3-7所示。

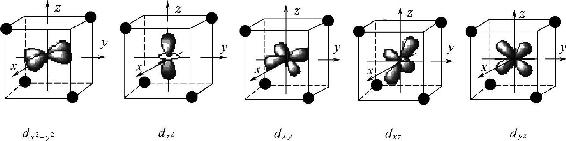
图3-7 四面体场中4个配体（以●表示）与金属离子5个d轨道的相对空间关系

金属离子的d_x2—y2和d_z2轨道分别指向立方体的面心，而d_xy、d_xz和d_yz轨道分别指向立方体各边的中心。显然，在四面体场中配体不是直接对着任何一个d轨道。d_xy、d_xz和d_yz轨道相对更靠近配体，受到的斥力较大，能量升高较多，形成一组三重简并的轨道，晶体场理论以dε表示。d_x2—y2和d_z2轨道离配体相对较远，受到的排斥较小，能量升高较少，形成一组二重简并的轨道，晶体场理论以dγ表示。这样金属离子原来简并的5个d轨道在四面体场中分裂成二组轨道，如图3-8所示。

图3-8 d轨道在四面体场中的能级分裂

3.平面四边形场中的能级分裂

平面四边形配合物中d轨道的能级分裂可从八面体场出发加以讨论。当八面体配合物中位于z轴上的2个配体同时外移时，八面体变形成为拉长八面体，最后配体完全失去时就变成平面四边形配合物。在这变化过程中，d_z2、d_xz和d_yz轨道受到配体的排斥变小，能量降低。同时，在xy平面上的配体会趋近金属离子，引起d_x2—y2、d_xy轨道能量的升高。这样d轨道在平面四边形场中分裂成四组轨道，参见图3-9。

图3-9 在不同晶体场中d轨道能级和分裂能的相对值/Dq （图中Δ_t、Δ_o和Δ_s分别表示四面体场、八面体场和平面四边形场的分裂能）

（三）晶体场分裂能

1.分裂能的定义

分裂能是一个重要的参数，可用来衡量配体场的强弱，并决定体系的能量、配合物的磁性和稳定性。在晶体场理论中，【将d轨道分裂后的最高能级和最低能级之间的能量差称为晶体场分裂能（crystal field splitting energy），以符号Δ表示】。Δ值可由量子力学理论计算，但通常是从配合物的光谱实验得出。因此，Δ值通常以光谱能量单位cm_—1（波数）表示（波数定义为波长的倒数；能量单位的换算关系为：1kJ·mol_—1=83.60cm_—1）。

2.影响分裂能的因素

（1）分裂能与晶体场对称性的关系 根据晶体场理论可以计算分裂后各d轨道的相对能量。为方便起见，晶体场理论令八面体场分裂能Δo=10Dq（下标“o”代表八面体），并设球形场能量E_球形场=0Dq，无论晶体场的对称性如何，d轨道在分裂前与分裂后的总能量保持不变。因此，在八面体场中，d轨道的能量应符合下列关系：

E（d_γ）—E（d_ε）=Δ_o=10Dq2E（d_γ）+3E（d_ε）=0由此可求得E（d_γ）=6Dq，E（d_ε）=—4Dq，即以E_球形场=0Dq为基准，八面体场中d轨道分裂的结果是d_γ轨道能量上升了6Dq，而dε轨道能量下降了4Dq。在四面体场中，配体不是直接对着任何一个d轨道，d轨道受到的静电斥力较八面体场小，

（下标“t”代表四面体）。因此，四面体场中d轨道的能量有下列关系：

E（d_ε）—E（d_γ）=Δ_t=4.45Dq2E（d_γ）+3E（d_ε）=0由此可求得E（d_γ）=—2.67Dq，E（d_ε）=1.78Dq。

图3-9中列出了八面体场、四面体场和平面四边形场中各d轨道的能级和分裂能的相对数值（以Dq表示）。晶体场理论同样能处理其他各种对称性的晶体场，这里不再进一步讨论。

一般来说，配合物的空间构型与分裂能的关系为：

Δ_{平面四边形}>Δ_八面体>Δ_四面体

（2）分裂能与中心原子和配体的关系 分裂能随中心原子和配体种类不同而异。现将从光谱实验测得的一些八面体配合物的Δo或10Dq值列于表3-5中。

从表3-5中的数据可以看出，分裂能与中心原子（金属离子）的电荷、所处周期以及配体的性质有关。一般有下列规律：

表3-5 一些八面体配合物的Δ_o或10D_q/cm^-1

①配体相同时，同种金属的离子电荷越高，Δ值一般越大。例如，[Fe（H₂O）₆]³⁺和[Fe（H₂O）₆]²⁺的Δ_o分别为14300cm^—1和10400cm^—1。这是由于随着金属离子电荷的增加，配体会更靠近金属离子，从而对d轨道产生较大的影响。

②配体和金属离子的电荷相同时，同族金属离子的Δ值自上而下增大。第二过渡系金属离子比第一过渡系金属离子的Δ增大约40%～50%；第三过渡系金属离子又比第二过渡系金属离子的Δ增大约20%～25%。例如，[Co（NH₃）₆]³⁺、[Rh（NH₃）₆]³⁺和[Ir（NH₃）₆]³⁺的Δ_o分别为22900cm^—1、34000cm^—1和40000cm^—1。这是由于后两系列过渡金属离子的半径较大，d轨道离原子核较远，较容易受到配体电场的影响，故Δ值较大。

③金属离子相同时，可将配体按照Δ_o值的大小排列为：

I^—<Br^—<S2^—<Cl—≈SCN^—<F^—<OC（NH₂）₂<OH^—≈ONO^—<C₂O²₄^—<H₂O<NCS^—<EDTA<py≈NH₃<en<phen≈NO2^—<CN^—≈CO

下面划线的为与金属离子配位的原子。这个顺序称为光谱化学序（spectrochemical series），它是从光谱实验总结得出的，主要适用于第一过渡系金属离子。通常将形成配合物时Δ值大的配体（如NO₂^—、CN^—）称为强场配体，而将Δ值小的配体（如I^—、Br^—）称为弱场配体。由光谱化学序可以看出，几种常见配位原子相对应的Δo值大致为：卤素<氧<氮<碳。

（四）晶体场中d电子的排布与成对能

配合物中金属离子的5个d轨道在配体的影响下发生能级分裂，电子在分裂的d轨道中的排布与分裂能和成对能的相对大小有关。

【当中心离子的一个轨道中已有一个电子占据时，要使第二个电子进入同一轨道并与第一个电子成对，必须克服电子间的相互排斥作用，所需消耗的能量称为成对能】。以符号E_P表示。金属离子的种类、电荷不同，其E_P不同。E_P可从光谱实验得出，见表3-6。一般来说，d⁵组态的金属离子有较大的EP值，电子不易成对；d⁶组态的金属离子E_P值较小，电子较易成对。

表3-6 一些过渡金属离子（d4～7）的成对能

在八面体场中，当金属离子的d电子数为d^1～3和d^8～10时，无论什么配体或E_P与Δo的相对大小如何，d电子的排布都只有1种，电子总是首先按洪特规则填入能量较低的d_ε轨道，再填入能量较高的d_γ轨道。但对于d^4～7，则有2种可能的排布：如果E_P>Δo，即配体场较弱时，电子成对所需的能量（E_P）大于电子从d_ε轨道进入d_γ轨道所需的能量（Δo），电子将不在d_ε轨道成对而是进入空的d_γ轨道，尽可能保持较多的未成对电子。这种【未成对电子数较多的d电子构型称为高自旋，相应的配合物称为高自旋配合物】。若E_P<Δo，即配体场较强时，电子成对所需的能量（EP）小于电子从d_ε轨道进入d_γ轨道所需的能量（Δo），电子将首先填满d_ε轨道，再将剩余的电子填入d_γ轨道，未成对电子数较少。这种【未成对电子数较少的d电子构型称为低自旋，相应的配合物称为低自旋配合物】。现将上述讨论列在表3-7中。

四面体场的分裂能Δt较小，约为八面体场的一半

，常常不易超过EP。事实上，已知的四面体配合物都是高自旋的。

表3-7 八面体配合物中中心原子的d电子构型

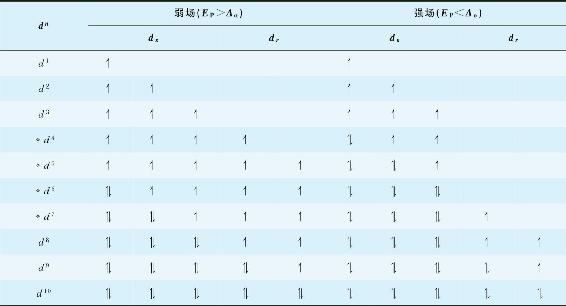
*因配体场强不同，d电子有高自旋和低自旋2种状态。

（五）晶体场稳定化能

【在晶体场作用下，金属离子d轨道发生能级分裂，电子优先填充在较低能量的轨道上，体系的总能量往往比d轨道未分裂时降低，这种能量的降低值称为晶体场稳定化能（crystal field stabilization energy）】。用符号E_C表示。以d轨道未分裂时的球形场能量E_球形场=0Dq为基准，按E_C=E_晶体场—E_球形场=E_晶体场，可计算各种不同d电子构型的中心原子在指定晶体场中的EC（以D_q和E_P表示，并忽略晶体场中E_P与球形场中E_P的差异）。

在八面体场中，d电子数为d^1～3和d^8～10的金属离子，如Ti³⁺（d¹）、V³⁺（d²）、Cr³⁺（d³）、Ni²⁺（d⁸）、Cu²⁺（d⁹）、Zn²⁺（d¹⁰），无论处于弱场（E_P>Δo）或强场（E_P<Δo），d电子的排布都只有1种。因此，它们在八面体弱场与强场中的E_C相同。例如：

V³⁺（d²）弱场或强场EC=2×（—4Dq）=—8Dq

Ni²⁺（d⁸）弱场或强场E_C=6×（—4Dq）+2×6Dq=—12Dq但是，d电子数为d^4～7的金属离子，如Cr²⁺（d⁴）、Mn²⁺（d⁵）、Fe²⁺（d⁶）、Co²⁺（d⁷），随配体场强不同，d电子有高自旋和低自旋2种状态。它们在八面体弱场中的成对电子数与球形场相同，故计算E_C时不考虑E_P的影响；但在八面体强场中的成对电子数大于球形场中的成对电子数，计算E_C时则应考虑EP的影响（八面体场与球形场中成对电子数的比较可参见图3-10）。例如：

图3-10 d电子在球形场和八面体场中的电子构型

Cr²⁺（d⁴）弱场（高自旋）E_C=3×（—4Dq）+1×6Dq=—6Dq

强场（低自旋）E_C=4×（—4Dq）+E_P=—16Dq+E_P

Fe²⁺（d⁶）弱场（高自旋）E_C=4×（—4Dq）+2×6Dq=—4Dq

强场（低自旋）E_C=6×（—4Dq）+2E_P=—24Dq+2E_P

在四面体场中，d电子数为d^1～10的金属离子都是高自旋的，且在四面体场中的成对电子数与球形场中相同（参见图3-11），故计算E_C时也不考虑E_P的影响。例如：

d²（高自旋）EC=2×（—2.67Dq）=—5.34Dq

d⁶（高自旋）EC=3×（—2.67Dq）+3×1.78Dq=—2.67Dq

图3-11 d电子在球形场和四面体场中的电子构型

现将八面体场和四面体场中d电子数为d_0～10的E_C（以Dq和E_P表示）列于表3-8中。对于平面四边形场中的E_C，可利用图3-9中的数据来计算。

表3-8 八面体场和四面体场中的EC

注：■因八面体强场中d^4～7的成对电子数与球形场中不同，故计算E_C时应考虑成对能E_P的影响。表中数据忽略了晶体场中E_P与球形场中E_P的差异。

由表3-8可知，在八面体弱场和四面体场中，具有d⁰、d⁵和d¹⁰构型的E_C均等于零，并且从d⁰～d⁵～d¹⁰的E_C呈现明显的规律性变化，近似为“双峰”形。在八面体弱场中，以d³和d⁸的E_C为最大，而在四面体场中，以d²和d⁷的E_C为最大。对于同一dⁿ构型，四面体场的E_C比八面体弱场的小。只要获得具体的八面体配合物、四面体配合物的分裂能和成对能的数据，以及d电子构型，代入表3-8中，就可得出它们的EC值。例如，由光谱实验测得八面体配离子[Ti（H₂O）₆]³⁺（d¹_εd⁰_γ构型）的分裂能Δo=10Dq=20300cm^—1，则[Ti（H₂O）₆]³⁺的E_C=1×（—4Dq）=1×[—（4/10）Δo]=—（4/10）×20300（cm^—1）=—8120cm^—1。按1kJ·mol^—1=83.60cm^—1换算，E_C=—8120（cm^—1）/83.60（cm^—1·kJ^—1）=—97.13kJ·mol—1。可见轨道分裂造成97.13kJ·mol^—1的能量降低，使体系更稳定。

第一过渡系金属（M²⁺、M³⁺）配合物的E_C值约为100～200kJ·mol^—1，接近许多共价单键的键能。因此，E_C是影响配合物性质的重要因素之一。但需注意，E_C仅占配合物总结合能的一小部分（约5%），仅考虑EC常不能合理地说明配合物的性质，还需考虑其他因素。例如，Fe³⁺（d⁵）形成的高自旋配合物的E_C为零，不能理解为这种配合物没有稳定性。此外，具有相同的空间构型、场强和d电子构型的配合物，都具有相同的以Dq和E_P表示的E_C，但具体的E_C值随中心原子和配体的种类不同而异。因此，只根据配合物的E_C有几个Dq而直接比较它们的稳定性，常会得出错误的结论。

（六）晶体场理论的应用

1.配合物的磁性

测量配合物的磁性可证实金属离子d电子数为d^4～7的八面体配合物有高自旋和低自旋之分。高、低自旋状态的未成对电子数不同，磁矩相差较大，未成对电子n可按近似关系

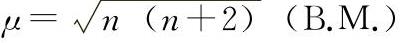
来确定。晶体场理论按分裂能Δ与成对能E_P的相对大小来推测：E_P>Δ时，高自旋；E_P<Δ时，低自旋。表3-9中列出了一些金属离子（d^4～7）八面体配合物的Δo和E_P以及磁性测定结果。由表可见，晶体场理论的推测结果与磁性测定结果一致。

表3-9 一些八面体配合物的自旋状态

注：表中n为金属离子的未成对电子数。

由于第二、第三系列过渡金属配合物的Δ值较大，它们几乎都是低自旋的，而第一系列过渡金属既能形成低自旋配合物，又能形成高自旋配合物。四面体配合物都是高自旋的。

2.配离子的空间结构

在过渡金属的配离子中，配位数为6的八面体配离子最常见。因为这种构型的配离子的配体数目较多，总结合能较大，且晶体场稳定化能也较大。但是，有些八面体配离子并非正八面体，而是变形八面体，如[Cu（H₂O）₆]²⁺、[Cu（NH₃）₄（H₂O）₂^]2+离子（经常以[Cu（H₂O）₄]²⁺、[Cu（NH₃）₄]²⁺表示）是拉长的八面体。在[Cu（NH₃）₄（H₂O）₂]²⁺中，Cu²⁺与4个NH₃处于同一平面且相距较近，而2个H₂O处于八面体相对的两顶点且相距较远。这种现象可用姜-泰勒（Jahn-Teller）效应来说明。

姜-泰勒效应指出：中心原子d电子云分布不对称的非线性分子中，如果基态时有几个简并态，则分子构型必然会发生某种畸变，以降低简并度而稳定其中某一状态。例如，形成八面体配离子时，若金属离子为d¹⁰构型，d电子云呈球形对称分布。若为d₉时，电子云分布就不对称了，这时可有两种简并状态的d电子排布方式：（d_ε）⁶（d_x2—y2）¹（d_z2）²和（d_ε）⁶（d_x2—y2）²（d_z2）¹。如果采用前一种排布方式，在xy平面上的4个配体受到的排斥比z轴上的2个配体更小，使xy平面上的4个键缩短，而在z轴上的2个键伸长，形成拉长八面体。相反，采用后一种排布方式，则会形成压缩八面体。实验表明，多数为拉长八面体。畸变还使原来简并的d_ε和d_γ轨道进一步分裂。如在拉长八面体中，d_γ轨道分裂为d_x2—y2（高）和d_z2（低）两个能级，而d_ε轨道分裂为d_xy（高）和d_xz、d_yz（低）两个能级。d电子填充这些分裂的轨道后会获得额外的稳定化能（但比E_C小得多）。

某些八面体配离子，由于姜-泰勒效应而形成拉长八面体。如果这种变形很显著，在z轴上的配体外移很远，就得到平面四边形配离子。d⁸构型的金属离子和强场配体结合时，有利于形成平面四边形配离子。这时8个d电子占据能量较低的4个轨道（d_xz、dy_z、d_z2、d_xy，见图3-9），而能级较高的d_x2—y2轨道空着，形成低自旋的配离子。配体场越强，d_x2—y2能级升高越多，因为它空着，对能量并无影响，而4个已占据轨道能级相应地降低较多（重心不变原理），配离子更稳定。典型的低自旋平面四边形配离子有[Ni（CN）₄]^2—、[PdCl₄]^2—、[Pt（NH₃）₄]²⁺等。

多数配位数为4的配合物为四面体构型。除d⁰、d⁵（弱场）、d¹⁰电子构型外，八面体的E_C都比四面体的大，但在四面体构型中，配体间的相互排斥作用较小。因此，在合适的条件下才能形成四面体构型的配离子。例如，[Zn（NH₃）₄]²⁺（d¹⁰）、[FeCl₄]^—（d⁵）、CrO²₄^—（d⁰）、[CoCl₄]^2—（d⁷）等都是四面体构型。

3.配合物的颜色

d电子数为d¹～d⁹的过渡金属离子的配合物一般是有颜色的。如各种金属离子的水合离子：[Ti（H₂O）₆]³⁺（紫红，d¹）、[V（H₂O）₆]³⁺（绿，d²）、[Cr（H₂O）₆]³⁺（紫，d³）、[Cr（H₂O）₆]²⁺（天蓝，d⁴）、[Mn（H₂O）₆]²⁺（肉红，d5）、[Fe（H₂O）₆]²⁺（淡绿，d⁶）、[Co（H₂O）₆]²⁺（粉红，d⁷）、[Ni（H₂O）₆]²⁺（绿，d⁸）、[Cu（H₂O）₄]²⁺（蓝，d⁹）等。配体不同时，配合物的颜色也会不同。如：[Co（NH₃）₆]³⁺（黄，d⁶）、[CoCl（NH₃）₅]²⁺（紫红，d⁶）、[Co（CN）₆]^3—（无色，d⁶）、[CrCl（H₂O）₅]²⁺（灰绿，d³）、[CrCl₂（H₂O）₄]⁺（深绿，d³）、[Cu（NH₃）₄]²⁺（深蓝，d⁹）、[CuCl₄]^2—（黄，d⁹）等。为什么各种配合物会呈现不同的颜色呢？

配合物显色的基本原因都是吸收了某些波长的光而呈现被吸收光的补色。图3-12是实用的圆形补色图，该图中某种颜色被吸收了，相对于它的颜色，即它的补色就会显现。配合物吸收光的原因有多种，其中之一是d-d跃迁。配合物中过渡金属离子分裂的d轨道没有填满电子时，在吸收某些波长的光后，电子可从较低能级的d轨道跃迁到较高能级的d轨道，这种跃迁称为d-d跃迁。d-d跃迁吸收光的能量一般在10000cm^—1～30000cm^—1（1000nm～333nm）范围，而可见光（750nm～400nm）正好在此范围。例如，[Ti（H₂O）₆]³⁺的可见吸收光谱中有一个宽吸收峰（见图3-13），从黄色到蓝色都存在强烈吸收（最大吸收峰位于20300cm^—1处），最少吸收的是红区和紫区，故显紫红色（被吸收光的补色）。晶体场理论认为，这是由d-d跃迁产生的，故Δo=10Dq=E（d_γ）—E（d_ε）=20300cm^—1。配合物不同，分裂能不同，因此由d-d跃迁产生的颜色也会不同。

图3-12 圆形补色图

图3-13 [Ti（H₂O）₆]³⁺的吸收光谱

晶体场理论提出了d轨道的能级分裂和稳定化能等概念，能较好地解释配合物的磁性、颜色（吸收光谱）等。然而晶体场理论存在明显的缺陷，它把金属离子和配体之间的作用完全归结为静电作用，因而无法解释由金属离子和配体之间的共价作用所产生的一些实验现象。例如，对于光谱化学序，若只考虑静电作用，阴离子配体应有较大的影响，但实际上许多阴离子的场强比一些分子弱，如OH^—的场强比H₂O的弱。近代实验表明，金属和配体之间存在轨道的重叠作用。因此，晶体场理论存在不足之处。后来在晶体场理论基础上发展形成了配位场理论，本教材不作介绍。