欧几里得《几何原本》

欧几里得独具慧眼，

一览无余地欣赏着美。他们很幸运，

尽管只那么一次，而且还是远远地，

依然闻到了镶嵌在宝石上的檀香

散发出的浓郁的香味。

E·圣·文森特·米莱（Edna St Vincent Millay）

有一个相对短暂的时期，泰勒斯、毕达哥拉斯、欧多克索斯（Eudoxus）、欧几里得和阿波罗尼奥斯（Apollonius）等这样一批伟大学者，创立了一门内容丰富、令人惊叹不已的第一流的学科——数学。这些人的赫赫声望，传遍了地中海地区每个角落，吸引了大批学生。师生们聚集形成学派，尽管这些学派的房舍很少，也没有校园，但却是真正的学术中心。这些学派传授的知识，统治了希腊人的整个文化生活，因此我们将从几个不同的方面介绍他们。

毕达哥拉斯学派最有影响，它决定了希腊数学的本质和内容。该学派领袖、富有传奇色彩的毕达哥拉斯，约公元前569年出生于萨摩斯岛。经过在埃及、印度的广泛游历，他吸收了大量的数学知识和神秘主义学说。后来，他在南意大利的希腊殖民地克罗托内（Grotone），建立了一个既信仰神秘主义，也信仰理性主义的团体。在神秘主义方面，这些人吸收了希腊宗教的精神，认为必须从腐败的物质中净化人的心灵，将精神从肉体的牢狱中拯救出来。为了达到这样的目的，毕达哥拉斯门徒信守独身生活。一丝不苟地举行赎罪仪式，遵守团体礼俗。除此之外，他们坚信必须遵守一定的禁忌。不穿毛纺衣服，不吃肉和豆子，除非是在宗教祭祀时可以例外，不接触白色公鸡，不坐在容积为一夸脱的量器上，不走大路，不用铁器去拨火，不在壶上留下有灰的印记。一旦灵魂从一个肉体中解脱出来，又可以在另一个肉体中获得新生。色诺芬（Xenophanes）说，一天，毕达哥拉斯碰到一条狗正在挨打，连忙喝道：“别打了，快住手，它是一个朋友的灵魂；我认出来了，我听到他在抱怨呢。”

这个团体主要致力于研究哲学、科学和数学。似乎预见到他们传授的某些知识可能会惹祸上身，因此他们要求新成员宣誓保守秘密，并终身不得退出。尽管其成员只限于男人，但却允许妇女听课，因为毕达哥拉斯认为女性也有其价值。这个组织的秘教性质、它的神秘主义以及秘密的仪式，激起了克罗托内人的怀疑和不满，最后，他们将毕达哥拉斯信徒们赶走，并烧毁了他们的房子。毕达哥拉斯逃到了南意大利的梅塔蓬图姆（Metapontum），据传，他在那儿惨遭杀害。但是，他的追随者却分散到希腊的其他地区，继续传播他的教义。

关于毕达哥拉斯其他神秘、玄乎的教义，将在以后的章节详细讨论。这里，我们将着眼于这样的事实：人们认为毕达哥拉斯主义者给予数学这门学科以特殊独立的地位。他们是第一次抽象地处理数学概念的人，尽管泰勒斯和他的依奥尼亚（Ionians）学派已经用演绎法确立了一些定理，但是毕达哥拉斯学派却独立地、系统化地运用了这一方法。他们使得数学理论从诸如大地测量、计算这样的实践活动中分离出来，而且证明了平面几何、立体几何、算术即数论中的基本定理。他们发现并证明了2的平方根的无理性，这使他们惊恐不已。

比毕达哥拉斯学派更广为人知的是柏拉图学院（园）（The Academy of Plato），该学院的学生以亚里士多德最为著名，后者在柏拉图去世后离开了该学院，自己创立了吕克昂（Lyceum）学校。我们知道，柏拉图早期的学生是他们那个时代最著名的哲学家、数学家和天文学家。在柏拉图的影响下，他们偏重纯数学，以至于忽略了所有广泛的实际应用，但却极大地丰富了各种知识体系。在数学、科学中的领先地位转移到亚历山大里亚后，该学院依然在很长一段时间里在哲学研究中起着主导作用。当这个学院在公元6世纪被查士丁尼（Justinian）皇帝取缔时，它已持续了900余年。

从小亚细亚到西西里岛、南意大利及整个地中海地区的许多学派和个人的工作，都被欧几里得总结在一本名为《几何原本》（Elements）的杰作中。这部最负盛名的著作，约在公元前300年形成，因为它既是几何学的逻辑表现形式，又构成了一个时代的数学史。从几条经过精心选择的公理出发，欧几里得演绎出了所有古典时期希腊大师们已掌握的最重要的结论，近500条定理。公理、编排顺序、表达的方式、一些所偏爱的课题的完成，这些都是欧几里得的贡献。

通过高中阶段的学习，我们对欧几里得《几何原本》中的大部分内容已很熟悉了。不过，在继续考虑它对文化的重大意义之前，我们将评述这本在历史上最富有影响的、并且在某些人看来具有反叛性的教科书的几个特点。现在，我们关心的是欧几里得《几何原本》的结构。

我们知道，几何学研究点、线、平面、角、圆、三角形，等等。对于欧几里得和希腊人来说，在这部著作中，欧几里得当时所给出的这些术语，并不表示物质实体本身，而是从物质实体中抽象出来的概念。事实上，来源于物质实体的数学抽象，仅仅只反映了物质实体的少量性质。拉紧的绳子可看作数学上的直线，而绳子的颜色、制成绳子的材料，却不是直线的性质。为了使抽象术语的含义更精确，欧几里得首先给这些术语下了定义。他将直线定义为两端保持平直的线，很显然，这一概念是从拉紧的弦、木匠的水平尺抽象而来的。他说，点，就是不包含任何部分的东西。按类似的方法，他定义了三角形、圆、多边形，等等。

欧几里得在下定义方面，走向了不必要、不明智的极端。一个具有逻辑结构的、自足的体系，必须从某一个起点开始。不能指望对每一个使用的概念都能给出定义，因为下定义就是用其他的概念去描述一个概念，而前者又必须通过其他的概念来描述。很明显，如果要使这个过程不至于循环，人们必须从一些未经定义的术语出发，来定义其他的术语。例如，欧几里得将点定义为不包含任何部分的东西，在这个定义中，“部分”本身的定义就不明确。其他的学者试图改进欧几里得的定义，将点定义为纯位置。那么，什么是位置呢？无疑，在某些社会领域，位置是生活中最重要的东西，但是，这种位置的概念并不能澄清点的意义。

再者，我们已经说了，并非所有的概念都能在一个独立的系统中得到定义。所有的概念都源于一定的物质实体，并且代表着这些物质实体。但是，物质的意义并不能给这种正式定义以任何帮助，因为它们并不是数学的内容。令人惊奇的是，几何学中的一些无法定义的概念，并没有给研究带来麻烦，我们马上将看到这一点。

欧几里得在对所要研究的概念给出定义后，至少他自己对此是感到满意的。接着，所要着手的最重要的工作，就是确立关于这些概念的事实或定理。为了进行这一演绎过程，他需要有前提，如同亚里士多德指出的那样：

并不是所有的东西都能被证明，否则证明的过程将会永无止境。证明必须从某个地方起步，用以起步的这些东西是能得到认可的，但却不是不可证明的。这些就是所有科学的第一普遍的原理，被人们称之为公理，或常识。

在公理的选择方面，欧几里得显示出了伟大的洞察力和判断力。在学派中起领袖作用的数学家们，从能够接受的公理着手进行选择。随着所选择的公理在数量上越来越多，危险性也就增加了。因为并不是所有的数学家都对其中所使用的公理的真实性确信不疑。另外，还有大量不必要的公理，从逻辑的角度看是一种浪费行为，因为最好是选择尽可能少的公理，并使得其他命题能从已被接受的公理中演绎出来。因此，欧几里得的任务就是为几何学寻求一套足够的、而且能被普遍接受的公理系统。而且，由于希腊人的几何研究是其研究真理的主要部分，因此这些公理必须是无可置疑的、绝对真实的。

欧几里得提出的公理，表述了点、线和其他几何图形的性质，而且这些性质为其相对应的实物所具有。很明显，所讨论的这些性质确实非常适用于物质实体，因此人们都愿意接受这些公理，并把它们作为进一步推理的基础。欧几里得选择的公理所具有的非凡优点，就在于尽管这些公理可被人立刻接受，但一点也不流于肤浅，因为它们导出了深刻的推论。而且，他所选择的公理非常有限，几条公理（总共才10条）却依然推演出了整个几何学系统的结构。

为了对欧几里得的选择的明智性加深认识，让我们来回顾一两条公理。他断言：“连接任意两点可作一条直线”；“过给定点和给定的中心可以作一个圆”；“整体大于其任何一个部分”。显然，这些都无懈可击，而且能被所有的人接受。

挑选出了几何学研究所涉及的概念，选择好了关于这些概念的基本公理之后，欧几里得开始着手建立定理、结论。当然，证明的方法是严格的演绎法。为了充分认识后人对欧几里得结论严密性钦佩的原因，让我们来欣赏他给出的一个证明。

欧几里得在其体系中，较早给出的一个定理是：一个等腰三角形，两底角相等。这个定理特别有趣。因为尽管它在本质上属于初等问题，但却代表了中世纪大学中几何学习的水平。这个定理被称做“笨蛋的难关”（pons asinorum）或“驴桥”（bridge of asses）因为笨蛋不能理解这个证明，就像一头在桥边的驴子一样，再也不能前进了。

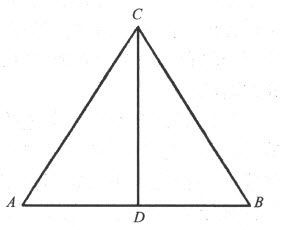
图4　一个等腰三角形

在欣赏证明之前，先考虑一下该定理的内容。如果ABC（图4）是一个等腰三角形，两腰AC和BC相等，我们希望证明底角A和B，也就是两条等边所对应的角相等。

证明是从引一条角C的角平分线CD入手的。这一步的合理性如下：欧几里得先前证明了任何角都能被平分。既然C是一个角，因此它也能被平分。这里的演绎推理是这样的形式：所有苹果是红的；这儿有一个苹果；因此这个苹果一定是红的。

引入线段CD后，就将三角形ABC分成了两个三角形ACD和DCB。我们知道，在这两个三角形中，首先AC等于CB，因为已知原来的三角形ABC是等腰三角形。第二，角ACD等于角DCB，因为CD是角平分线。第三，因为CD是两个小三角形的公共边，所以这两个三角形有一条等边。因为前面（系指在《几何原本》中）有一个定理断言，任何两个三角形，如果一个三角形的两边和这两边所夹的角，与另一个三角形的两边和这两边所夹的角相等，则这两个三角形全等。由于所讨论的两个三角形有这些相等的部分，因此这两个三角形全等。最后我们断言，角A和角B相等，因为全等三角形的定义，正是对应的部分都相等，角A和角B就是这样的对应部分。

这样，这一定理就通过几个演绎论证证明了，其中每一步都利用了无可置疑的前提，从而得出了无可置疑的结论。当然，在欧几里得那里，并不是所有的证明都如此简单。但是，任何一个证明，无论第一眼看上去如何复杂，都只不过是由一系列简单的演绎论证组成的而已。

我们不必逐个重新考查欧几里得确立的定理。需要指出的是，从公理出发，一些简单的定理立刻就能得到证明，这些定理就成了那些更深奥的定理的基石，这样，整个一座精美的大厦就严密地建立起来了。的确，许多学生不禁感慨万分：这么多看似复杂的定理，竟能从少数几个自明的公理推导出来，真是不可思议！

下一步，看看欧几里得关于物体的大小、形状的基本性质的研究内容。他首先关注的是，在什么条件下，两个物体的大小、形状相同，也就是在什么条件下这些物体是全等的。例如，假设一位测量员测量两块地，形状为三角形，他怎么确定这两块地是否相等呢？他必须测量每条边、每个角，甚至两块地的面积后，才能判断它们是否相等吗？要是这样，就用不着欧几里得的定理了。例如，如果已知两个三角形中的对应边相等，那么这两个三角形就在所有各方面都相等。这一事实似乎不过是一件微不足道的小问题，但是读者会看到，如果问在什么条件下，两个四边形，即两个具有4条边的图形全等，情形就不完全一样了。当然，这样的问题以及相关的问题，适用于所有各种几何图形。

欧几里得接着问道：如果图形不相等，那么它们之间彼此又有什么重要的关系呢？它们之间又有哪些共同的几何性质呢？他主要考虑的是形状关系。大小不等、但形状相同的图形，即相似形，有许多共同的几何性质。例如，对三角形来说，相似意味着，一个三角形的角与另一个三角形相对应的角相等。从这个确定的性质出发，就可以得出结论：任意两条对应边的比是常数。这样，如果ABC和A′B′C′是相似三角形（图5），则AB/A′B′等于BC/B′C′。而且，如果在这两个三角形中，两条对应边的比是r，则两者面积之比是r²。

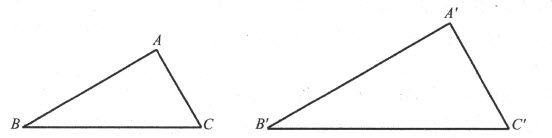
图5　两个相似三角形

如果图形形状和大小都不相同，那么它们之间还存在什么关系呢？当然，它们可能有相同的面积，用几何学术语说，就是等积的。或者它们可以内接于同一个圆中。它们之间可能的关系和彼此间相关的问题不胜枚举。欧几里得选择了其中最基本的关系。

对于所有研究的概念，欧几里得不仅将其应用于由直线构成的图形，而且也应用于圆和球。他对于这些图形的浓厚兴趣耐人寻味。因为在希腊人看来，圆和球是最完美的图形。

从美学欣赏的观点出发，另一类有吸引力的图形同样使他们着迷。在三角形中，等边三角形值得引人注意，因为它的所有边在长度上都相等，所有的角的大小都相同。同理，在四边形中，正方形最富有吸引力。在具有五边、六边和多边的平面图形中，以能够作成具有相同的边和角的图形最富有吸引力。这样的图形称为正多边形，人们对它们作过详细的研究。立体图形也有类似的情况。立体封闭的表面能够由正多边形形成，任何一面只能由同一种多边形构成。例如，一个立方体的表面就由沿边相连的六个正方形组成。一个多面体，如果有像立方体这种类型的表面，则称之为正多面体。

与正多面体有关的第一个问题是，有多少种不同类型的正多面体？经过严格的推理，欧几里得证明了，存在且只存在5种正多面体。证明过程在这里就不再重复了。图6中的5种图形就是这些正多面体。柏拉图非常推崇这些图形，他甚至认为，神也会运用这些图形。于是，他详细阐述了某个希腊学派的思想，该学派宣称，所有的物质都由土、气、火和水4种元素构成。柏拉图则更进一步认为，火元素是四面体，气元素是八面体，水元素是二十面体，土元素是立方体。第五种形状——十二面体，被神保留下来作为宇宙本身的形状。

希腊人还仔细研究了另外一类曲线。我们都熟悉圆锥状图形，例如冰淇淋就呈圆锥形。如果有两个非常长的圆锥体，如图7所示放置，则可得到数学家称为圆锥表面的图形，或者有时简称为圆锥体。这个圆锥表面由两部分构成，它们从O点向两方无限延伸。如果圆锥表面被一个平面所切（仅仅是一个像桌面一样光滑、没有厚度而且可以向所有方向延伸的表面），那么相切所产生的曲线，其形状取决于平面相对于圆锥的位置。当平面完全切过圆锥的某处时，横断面的曲线是椭圆（图7中DEF），或者是一个圆（图7中ABC）；如果切割的平面倾斜，切过圆锥的两部分，那么横断面的曲线由两部分组成，称为一组双曲线（图7中RST、R′S′T′）；最后，如果切面与圆锥的任意一条线如POP′平行，则横断面的曲线就是一条抛物线（图7中GIK）。

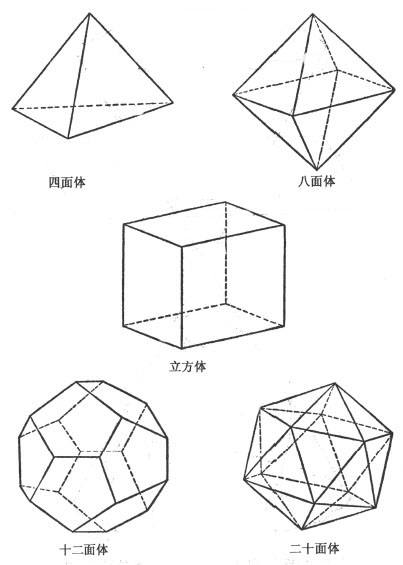
图6　5种正多面体

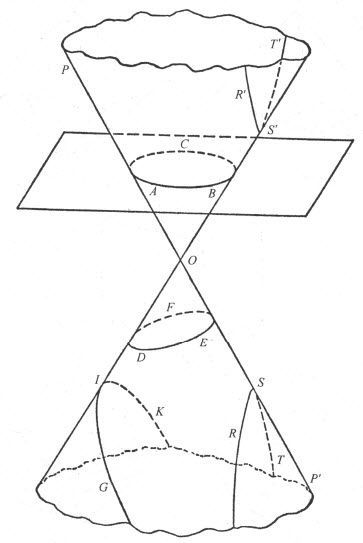
图7　圆锥表面和由其相切平面所成的圆锥曲线

欧几里得以类似的方法，将有关圆锥曲线的基本事实加以归纳收集，并整理成书，但这部书失传了。在欧几里得稍后不久，另一位著名的数学家阿波罗尼奥斯，就又写了关于圆锥曲线的一部著作，对欧几里得的学说进行了深化、扩充，他也因为该书而著称于世，就像欧几里得因为其《几何原本》流芳百世一样。在这个古典时期，还有一些学者写成了许多其他的数学著作，可惜只有少部分幸存。根据现有的书籍和残篇来判断，完全可以断定，这个时代是一个富有巨大创造力、对数学有着强烈兴趣的时代，是历史上无与伦比的光辉灿烂的时代。

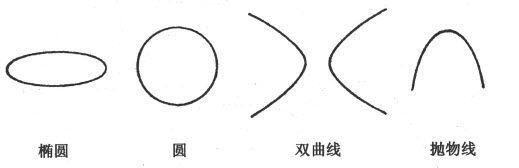
图8　圆锥曲线

在希腊数学中，无论是业已提出但尚未解决的问题，还是已经提出并获解决的问题，在这些问题中，有3个众所周知的著名问题。它们被称为“化圆为方”、“倍立方”和“三等分任意角”。化圆为方的意思是作一个正方形，其面积与一个给定圆的面积相等。倍立方，就是构造一个立方体，其体积是已给定立方体体积的两倍。最后，三等分任意角，就是将任意一个角分为相等的三部分。这些作图问题，限于仅仅使用一把直尺——一根没有刻度的直尺，一支圆规，不允许使用任何其他的工具。

对作图工具的限制，表明了古希腊人对待数学的态度。直尺和圆规是直线、圆的实物对应物。总的来说，希腊人在研究几何时，都是仅仅限于直线、圆这两种图形，以及由此直接导出的图形。我们将看到，即使是圆锥曲线，也是通过一个平面切过一个圆锥而得到的，这些图形中的平面和圆锥，都能由一条移动的直线生成。这种对直线、圆的自我约束、非理性的限制，目的是为了保持几何学的简单、和谐，以及由此而产生的美学上的魅力。

以柏拉图为代表的某些希腊学者，还以其他同样重要的理由来强调这种尺规作图的限制。按照他们的观点，引入更复杂的工具，来解决这些作图问题，对于进行手工绘制是可取的，但对一个思想家来说则是不足称道的。柏拉图更进一步认为，利用复杂的工具，“几何学的优点”就会荡然无存，因为这样我们又重新使几何学退到了感性世界，而不是用思想中永恒的、超越物质的思维想像力去提高、充实它。在他们看来，上帝之所以是上帝，就是因为使用了这种图形。

这3个作图问题在希腊非常流行。据历史上第一次有关这些问题的记载，哲学家安那克萨哥拉（Anaxagoras），在狱中曾花了相当长时间，试图解决化圆为方的问题。尽管最优秀的希腊数学家做了种种努力，仍未能解决这一问题。在这之后的2000多年，这些问题依然悬而未决。在大约70年前，终于有人证明，在给定条件下，不可能作出这些图形⁽¹⁾。尽管这已成为事实，但人们仍在试图解决这些问题，而且经常声称已取得成功，不需要考查他们的工作，我们就能断定他们是错误的，或者他们对这些问题的理解是错误的。

对这些著名问题的孜孜不倦的探求，表明了数学家们严谨的治学态度、坚忍不拔的精神。这些问题并没有实用的意义，因为只需使用比没有刻度的直尺和圆规稍微复杂一些的工具，就能轻而易举地作出这些图形。然而，正是人类这种不可抑止的迎接智力挑战的激情，使得数学家们试图去解决这种理论上的作图问题。

确实，歪打正着是常有的事。为现代天文学开辟了道路的圆锥曲线，就是在探索解决这些著名的作图问题的方法时发现的，在这一过程中，还得出了许多其他有用的、美妙的数学结论。事实上，如果仅仅列举出那些通过解决脱离实际的、“毫无价值”的问题而得到的主要数学思想，就有可能会将数学定义为日常琐事的流水账（许多“教育家”，尽管对数学及其历史一无所知，但却毫不犹豫地作出了这种评价）。有关这些问题研究的历史表明，那些对“脱离实际”的希腊人的指责，很不公正。因为这些幻想家对于当今科学时代的进步所做出的贡献，比起那些所谓的注重实际的人们所做的工作而言，的确要大得多。

我们已经赞扬了希腊人，他们使得数学抽象化了。这样将有助于我们在数学的范围内，理解这种抽象的含义，至少对欧氏几何是如此。

考虑一种相当简单的情形。假设选定任意给定的两点A和B，一条不过A或B但是与这两点在同一个平面上的直线L（图9）。另外，假定要在直线L上找一点P，使得AP＋PB的值（距离）最小；即如果Q是L上的任意另外一点，那么AP＋PB必须小于AQ＋QB。这是一个纯几何问题。不难证明，如果选择这样的P，使得AP，BP与直线L所成的角相等，则距离AP＋PB的值最小。

图9

姑且承认这一定理的证明毫无问题，再看一看这一定理如何应用于实践中。假定A，B是两个城市的位置，L是一条河。沿这条河建造一个这两座城市共同使用的码头，要使得从该码头到A城市与到B城市的总路程尽可能的短，那么这个码头应该确定在沿河的哪一点？我们上述的普遍性定理给出了答案：该点就是使得AP，BP与河流成等角的点P。

再考虑另一个“实用的”情形。击一个位于球桌上A点的桌球，使得该球从球桌的边L弹回时击中位于B点的球。桌球总是按这样的路径运动：桌球碰及桌边时的路径与桌边形成的夹角，与反弹时形成的夹角相等。就是说在图10中，角1等于角2。每个击桌球的人，至少在潜意识中知道这个事实，并加以运用，直接把球对准点P，使得AP，BP与桌边成相等的角。然而可以肯定，他并不知道所选择的和希望球将运行的路线，是球从A出发到球桌边弹回到B所经过的最短路线。

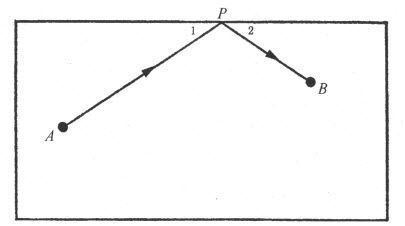
图10

我们所举的例子表明了一个数学定理如何在两种极不相同且毫不相关的情形中得到了运用的情况。事实上，该定理还有大量其他的应用。为解决一个领域中的问题而得到的定理，经常能卓有成效地应用于另一个完全不同的领域，这样的事情在数学史上比比皆是，令人惊奇不已。当然，数学的这种应用的广泛性，是以抽象作为代价而获得的。为了通过研究理想三角形而得到关于所有三角形的定理，数学家不得不与扑朔迷离、难以捉摸的抽象思维打交道，而不能仅仅研究用木头做成的三角形图案。

研究抽象的数学定理与其应用的关系，还应注意非常重要的一点：抽象的定理表示的是理想情况，而在实际情况中运用该定理，则有可能与理想情形相去甚远。例如，假定在地球的表面放置一个三角形，我们能够将平面几何的定理运用于该三角形吗？首先，地球是球形而非一个平面，而且地球的表面也很难是一个标准的球面，而是相当不规则的球面。于是，至少由于这两个原因，地球表面的这个三角形与平面几何中的理想三角形相去甚远。因此，在运用数学定理时，就可能产生一些误差。只有在实际三角形接近理想情形时，才可以利用数学理论。如果在实际运用时忽略了这一事实，就有可能导致严重的误差。

欧几里得几何的创立，对人类的贡献不仅仅在于产生了一些有用的、美妙的定理，更主要的是它孕育出了一种理性精神。人类任何其他的创造，都不可能像欧几里得的几百条证明那样，显示出这么多的知识都是仅仅靠推理而推导出来的。这些大量深奥的演绎结果，使得希腊人和以后的文明了解到理性的力量，从而增强了他们利用这种才能获得成功的信心。受这一成就的鼓舞，西方人把理性运用于其他领域。神学家、逻辑学家、哲学家、政治家和所有真理的追求者，都纷纷仿效欧几里得几何的形式和推演过程。

甚至在希腊人中间，数学也被看作是所有科学的标准，亚里士多德特别强调，每一门科学都必须像欧几里得的几何学一样，通过一些适用于这门科学的有效方法，确立几条基本原理，从这几条基本原理中，以演绎的形式推导出真理。在柏拉图学院的门口，写有这样的箴言：“不懂数学者不得入内”，这典型地反映了他们对待数学的态度。

西方人从欧几里得的《几何原本》中，学会了怎样进行完美的推理，怎样获得在几何学方面的技巧，以及怎样区别精确的推理与仅仅只不过是进行自称为证明的夸夸其谈的那些不严格的推理。在几何学这门学科的发展过程中，希腊人认识到了一般的推理规律，其中三段论现在已是众所周知的了。他们也发现了解决问题的一般方法。例如，柏拉图被认为发明了分析方法，这种方法是从假设结论成立开始，逐步进行演绎推理，直到已知的事实。然后，将所进行的推演步骤反过来，就给出了正确的证明。读者可能能回忆起，在学习欧氏几何时自己曾用这种方法证明了某个定理。当然，这一方法的应用超出了几何学领域。希腊几何学家也发明了间接证明方法，并发现了这种方法的作用，他们对此深深地引以自豪。这种方法是，在可能的情形中，搜索出所有可能的假设，除正确的那个假设外，所有其他的假设都将导出矛盾的结论，因此就可以剔除这些错误的假设。这种方法的逻辑基础即逻辑学家熟知的矛盾律和排中律，就是由亚里士多德形成为公式的。

精确的定义，清楚明白的公设，严格的证明，在几何学研究中的必要性与日俱增，日益明确。诸如苏格拉底、柏拉图等人不仅强调这些必要性，而且他们还对数学的优雅、完整和清晰的结构做出了贡献。实际上，希腊人将几何学知识运用在逻辑方面的伟大实践，被亚里士多德结构化、系统化了，总结成了思维的规律，这些思维规律已为我们接受并被我们广泛应用。因此，希腊几何学被尊崇为逻辑科学的始祖。

从希腊时代以来，几百代人通过学习欧几里得几何学，掌握了如何进行推理的方法，然而，这一学习过程曾遭到许多人的反对，这些人争辩说，我们不学习数学也能学会逻辑。这种观点的理由和下面这种观点是一致的：由于我们所有的人都能构思出伟大的油画作品，因此，在这个世界上所存在的油画作品的构思，也许和油画作品本身一样丰富多彩。不幸的是，油画的构思从来也没有能打动人的心弦。

欧几里得几何学的重要性，远远超出了作为逻辑实践和推理模式本身的价值。以前，数学只不过是推动其他领域进步的工具，随着几何学美妙结构和精美推理的发展，数学变成了一门艺术。希腊人就是这样欣赏数学的。算术、几何、天文学对他们来说，就是音乐之于精神、思维之于艺术。

的确，在希腊思想中，很难把理性因素与美学因素、道德因素分开。我们一再看到，因为球是所有形体中最美丽的形状，所以地球一定是球形的，因而也是神圣的和完美的。由于同样的理由，柏拉图坚信，太阳、月亮、星星都各自被牢牢地固定在一个球体上，而且它们在自身的轴上绕地球旋转。另外，每个星体的轨道也一定是圆形，因为圆和球具有同样美的魅力。与在不完美的地球上所充斥的直线运动形成鲜明对照，天空中永恒不变的秩序，所呈现出的是圆形和球形的轨迹。美学原因和道德原因也决定了天体运行的速度必须一致，在相同的时间间隔内，运行的距离必须相等。这种庄严、规则、从容不迫的运动正适合于天体。事实上，毕达哥拉斯学派曾坚持认为，变速运动是行星所不能容许的；“即使在人类的社会中，这种不规则的行为也与一个绅士的风度相去甚远”。按照亚里士多德的解释，科学的真理与诗歌中的真理是一致的，或者说，自然界的目的，与其特有的规律在绝大多数情况下总是趋于一致，或呈现为另一种美妙的形式。

几何、哲学、逻辑、艺术，所反映的是一种思维方式，一种世界观，因此，像有些历史学家那样去探寻古典希腊文化在所有这些领域共同存在的特征，是十分迷人的课题。例如，清楚明晰、简洁的欧氏几何结构，是清晰、有条理的设计在数学上的表现，这种爱好也体现在希腊人质朴、简单的庙宇的形式中。相比之下，哥特式大教堂则以其繁琐的内外结构而显得复杂无比。古典时期的希腊雕刻也是惊人的十分简练。没有多余繁杂的衣裙服饰、军功勋章、花纹褶边堆砌在塑像上，这些东西只会影响表现其基本主题。

同样，这个时期的古典文学创作具有简练、清晰、求实的风格，比喻和形容词的使用显得恰如其分。我们只要比较一下现代人对夜莺歌唱的描写，以及古希腊人对鸟儿欢唱的赞美，就可以看出希腊风格的实质。现代人如此形容歌唱的夜莺：“它的歌声，在那美妙孤独的地方，在那神奇的窗口，产生迷人的魅力，漂向险恶的一望无际的大海的波涛上。”古希腊悲剧作家索福克勒斯（Sophocles）笔下的鸟则是：“它深深地隐藏在绿色的长满青藤的树丛中，唱着清晰嘹亮的歌曲，它似乎要躲避阳光，还有那风吹声。”从中我们可以看出希腊风格的实质。清晰、简洁、谨严是美的各种因素。希腊艺术是智慧的艺术，是清晰的思想家的艺术，因而是质朴的艺术。的确，古希腊的几何学、建筑、雕刻、文学达到了一种超越其自身的简单质朴的美的境界。

欧氏几何经常被描绘成是封闭的（closed）和有限的。这些形容词有几层意思。这门科学本身是有限制的，如我们已经看到的那样，图形利用圆规和直尺就能作出，定理则能从一组固定的公理中推导出来。在欧氏几何中进行推理时，没有引进新的公理。欧氏几何避免了无穷，因此在这个意义上它也是有限的。例如，欧几里得并不对直线整个地进行考虑，而将直线定义为一条可以向两个方向延伸至充分远的线段，他似乎对延伸这一点也只是勉强同意。同样，在处理全体整数的时候，希腊人也将其看作是潜力无穷（potentially infinite），即仅仅在这样的意义上是无穷的：对于任意给定的有限集合，总是可以加进更多的数，他们并不将全体整数自身当作一个完整的集合，而对它进行研究。

这些封闭、有限的特征，在希腊建筑中也占据了支配地位。希腊庙宇的整个结构小巧玲珑、一览无余。给人的印象是终极、完美而明快。只需看一眼，思维立刻就能抓住，把握其比例和优美的结构。希腊庙宇与哥特式建筑相比，后者几乎永远也不能被想像为是一个整体。它似乎在各个方向都消失，使人无法对其有一个总体的把握。它显得深邃，通过塔顶，又显示出了神圣的希望。通过向后倾斜的拱门，人们可以看到无穷无尽的远景，其内部又好像是来自远处的幽暗、高高的祭坛，从而能激起人们的想像，人们的敬畏之情油然而生。庞大的物体能使人想起那不可见的、虚无飘渺的情景。高大的建筑吞没了单个的个人，使人融入其内部，这时有限感也就消失了。

在希腊科学中，无穷的概念几乎不被人们理解，并且人们都很自然地避免使用它。对于希腊人来说，最简单的运动形式，并不是像我们今天认为的作直线运动，因为从整体上来说，直线并不是能感觉得到的，直线运动永远不会终结。希腊人偏爱圆周运动。无限过程这一概念使他们困惑，因此，他们在“宁静的无限空间”面前退缩了。

在哲学中，希腊人也回避无穷概念。无穷悖论，有些是后面将要讨论的，显然对希腊哲学思想来说是不可逾越的障碍。亚里士多德说，无穷是不完美的、未完成的，因而是不可想像的，它毫无形状、容易混乱。事实上，善、恶的观念是这样确立的：善是有限的、确定的，而恶是无限的、不确定的。物体的有限性、确定性，为该物体注入了个性，并使之完美。只有当一个物体是确定的、有限的时，该物体才具有本质的规定，才具有意义。索福克勒斯说：“芸芸众生，万事万物，被人诅咒后才为大众所知。”

希腊数学的另一个特征也贯穿于文明长河之中：欧氏几何是静态的。它不研究变化图形的性质。在整个图形给定之后，才进行研究。希腊庙宇的宁静气氛反映了这种特征。思想、精神在那里都处于安宁状态。同样，希腊雕刻中的图像也是静态、冷漠的，给人以一种心理上的安怡，如同等边三角形唤起的情感一样。米隆的“掷铁饼者”（插图2）中，主人公正准备发出巨大的力量，却还像人们熟悉的正在品茶的英国绅士一样，安宁、从容不迫。

人们也经常指出希腊戏剧中的静态特征。很少或几乎没有动作。戏剧一开始，那些导致剧中人所面临的问题或困境的事件，只是简要地给观众介绍一番而已。戏剧本身所关注的是心灵上的斗争，而很少关注动作，结局也总是能为人们预先猜到。

与希腊戏剧的静态特征相关联，欧几里得几何还有另一个特征。希腊悲剧强调命运、必然性的作用。在一出戏剧中，剧中人似乎没有意志、力量独立地作出一个决定，而是都受着隐藏着的力量的支配。正因为如此，俄狄浦斯（Oedipus）被迫残忍地乱伦，杀父。命运的作用，与利用演绎推理的先天的必然性是一致的。从前提出发，数学家不能自由地选择结论，只能不得不接受必然的结论。

希腊艺术、几何、哲学还有另外一个重要的特征，这一特征虽然在这些领域的创造活动中经常可见，但是却是希腊人取得卓越成就的一个方面。他们的成就反映了这样的事实：他们努力去寻求宇宙的美（他们首先努力寻求宇宙的美，其次才寻求宇宙的真）。他们追求的是最普遍和永恒的知识，而不是个别的和转瞬即逝的知识。数学领域是永恒的，因此其中的数学性质将永远有效，这个领域的知识最称心合意。水泡和五彩斑斓的彩色气球，尽管它们可能很迷人，但却是不值得重视的，因为它们很快就会破灭。古典时期的希腊艺术努力反映、描绘的不是单个的人，而是人类普遍的、基本的特征。对于任何一个人，至关重要的是他所体现的人类一般特征。个人的日常活动，人们之间的相互关系，以及服装，所有这些都只具有偶然性，是琐碎小事。在希腊人的哲学探索中，他们寻求确定和理解概念、性质的最完美的形式，因为完美本身就是永恒的。最完美的状态是值得思索的；由此出发，希腊社会的民主化，就是一个顺理成章、易于理解的问题。

到现在为止，我们已经考察的数学和它所反映的文化属于古典希腊时期。但这决不意味着，“文明的摇篮”对数学、对我们人类生活和思想的贡献到此为止。从公元前300年延续至公元600年的这一重要时代依然有待我们去探讨。在结束这一章之前，让我们以现代人的眼光回顾一下这一在数学方面富有创造力的时代。坚持以演绎方法作为惟一的证明方法的，注重抽象而不注重个别事物，选择最富有成果、具有最高可接受性的公理系统，这些决定了现代数学的特征。巧妙的猜想、大量十分重要的定理的证明，在数学发展中起了很好的作用。同时，数学和来源于人类理性的卓越光辉的真正激情，第一次被希腊人激发了。他们的数学成就表明，在人类活动中，思想具有至高无上的作用，而且由此提出了文明的一个新概念。

————————————————————

(1) 1837年，P·L·旺策尔（Pierre Laurent Wantzel，1814－1848）给出了“三等分任意角”、“倍立方”两个问题不可能性的证明；1882年，F·林德曼（Ferdinand Lindemann，1852－1939）证明了圆周率π的超越性，从而给出了“化圆为方”问题的不可能性的证明。1895年，F·克莱因（Felix Klein，1849－1925）给出了三大问题不可能性的简单而清晰的证明。——译者注