新几何，新世界

我已得到了如此奇怪的发现，使我自己也为此惊讶不已：我已从乌有中创造了另一个新世界。

J·鲍耶（John Bolyai）

 

第一个向欧几里得挑战的是欧几里得自己。这位被人们最为普遍接受的思想体系——永恒的真理、哲学与科学的摇篮——的创造者，甚至在将他的思想体系公之于世之前，就对其结果提出了怀疑。欧几里得自己的疑虑，标志着2000年来从“幕后”攻击为人们广泛接受的、显而易见真理的开端。

众所周知，欧几里得几何学以10条公理为基础，这些公理的真理性不证自明、不言而喻，所以没有一位“神智健全”的人胆敢对此表示怀疑。从如此坚实的基础出发，经过完美、严谨的逻辑推理，从而产生出了更多的“真理”，它们也像公理一样，富有吸引力，并能立刻为学者们广泛地接受。由于牛顿时代的成功为这些真理增添了坚实、充分的无可置疑的证据，从而使这些真理在2000多年的应用中达到了光辉的顶点。许多世纪以来，为经验所支持的逻辑和为传统所支持的常识，使得人们把欧几里得体系当作神圣不可侵犯的圣物。到1800年时，受过良好教育的人更加愿意对着欧几里得定理发誓，而不愿意对着《圣经》的经文发誓。

无论是诉诸于经验、信仰康德哲学的人，或者明显地持反对态度的人，都毫不迟疑地得出了这样的结论：欧氏几何是真理，真理就是欧氏几何。尽管有这样令人羡慕的评价，但从其诞生时起，随着时光的流逝，欧氏几何一直令包括欧几里得在内的少数人忐忑不安。他们被两条显然是无懈可击的公理困惑着。

第一条公理说，一条直线线段能够在两个方向随意延长。第二条公理是平行线公理，这条公理说，通过不在直线L上的一点P，有且仅有一条直线M（在P和L的平面上），无论M和L延长多远，M都不会与L相交（图77）。如果欧氏几何的公理为人们所接受，是由于物理空间的经验迫使我们不得不如此，那么这些公理就开始值得怀疑了。任何人直接经验的范围都没有超出地球上几英里。真正能肯定的是，这些公理在我们实际生活的有限区域内似乎是真理。甚至在这样的范围内，我们也不能肯定地断定这些结论，因为如同我们在讨论射影几何的那一章里所指出的那样，即使在我们周围最近的空间中，我们也绝对看不到平行线束。当我们看远距离的欧几里得所描述的平行线时，发现这些平行线似乎相交了。

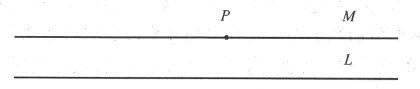
图77　欧几里得的平行公理

欧几里得在利用这些公理的过程中，显示了他对这些公理的关注。平行公理是两条令人疑虑的公理中最值得怀疑的，他在证完了许多无需用平行公理的定理之后才使用它。他同样关注直线的无限延伸性。考查他的几何定理，结果表明，他的确利用了线段（两点之间的直线），但是从未假设过最初的公理中所出现的无限长的直线。当必须将线段沿两个方向延长时，也仅仅只延长到定理所需要的长度为止。这并不能由此推断出欧几里得怀疑这些公理的正确性的结论；而是因为他这样做似乎强烈地暗示，他的确喜欢从更简单的公理中推导出结果。

在每个时代，都有一些过于严谨的思想家，他们像欧几里得一样，也在利用公理时表现得犹豫不决，就像讲求实际的商人将赌上他的家当一样小心。为了消除困扰心头的疑虑，这些人从密苏里（Missouri）开始就都在尝试着做同样的努力。他们集中于讨论平行线公理，试图从其他公理中推导出平行线公理，或者找出一条更能为人们所接受的公理替代平行线公理。数百名最优秀的数学家做出了最有价值的努力，但都以失败告终。到1800年时，平行线公理已经成了几何学瑕玷的标志。

评论人们所做的大多数努力几乎没有必要，也没有多大益处。但是，耶稣会牧师G·萨凯里（Girolamo Saccheri）的工作却值得我们注意。他是比萨大学的数学教授，一位爱好逻辑的学者。萨凯里有一个崭新的想法。他的新奇之处就在于，把平行线公理归结为事实上讨论这样的问题：给定一条直线L和一点P，那么或者（a）恰好有一条通过P且平行于L的直线；（b）没有过P平行于L的直线；或者（c）至少有两条过P平行于L的直线。选择（a）就是欧几里得的平行线公理。假设它被（b）所代替，若后者与欧几里得的其他9条公理组合在一起，将被证明推导出了相互矛盾的定理。这样，选择（b）肯定是不正确的。同样，如果选择（c）和另外9条欧氏公理也推导出了矛盾的定理，则选择（c）也是不正确的。那么，这样一来就意味着，欧几里得的平行线公理是惟一可能的。

选择（b）与其他9条欧氏公理，萨凯里的确推导出了互相矛盾的定理。但是，从9条欧氏公理和选择假设至少存在两条平行线的公理（即选择（c））中，他没有导出矛盾的结论。尽管他的努力是决定性的、富有成效的，尽管他所推导出的结论与欧氏几何的类似结论相比是令人惊奇的，但结论之间的确没有矛盾。

萨凯里正处于做出划时代发现的门槛上，但他拒绝迈出这一步。现在，我们把萨凯里应该导出而没有导出不一致性这一结论留给读者。就萨凯里本人来说，他对从自己的一套公理中获得的奇怪的定理毫无思想准备，以至于他认为欧几里得的平行线公理必定是正确的。正因为如此，他于1733年在一本名为《无懈可击的欧几里得》（Euclid Vindicated from All Defects）的书中发表了他的结果。很显然，当一个人开始为另一个人辩护时，他将很有可能这样做：不顾事实。

关于萨凯里以及许多其他人失败的一个解释是，这些伟大的数学家都接近了平行线公理所提出的问题，然而谁都没有足够的判断能力认识到，必须抛弃2000多年的思维习惯。但是，19世纪初叶，在数学科学内部发生了一场知识背景的变革，对基本信念进行了一场彻底的清查和批判性的再考查。无疑这场变革是因为这样的事实：高斯、N·罗巴切夫斯基（Nicholas Lobatchevsky）、鲍耶3人，在相互不了解各自思想的情况下，大约同时各自发现了萨凯里工作的正确意义；罗巴切夫斯基和鲍耶各自在几年之内发表了他们的成果。

这3人中最伟大的，并能与牛顿和阿基米德并驾齐驱的人是高斯。高斯在许多领域都表现出了令人难以置信的早熟，尤其是在他喜爱的数学方面。当他还是一位少年的时候，就证明了能用直尺（没有刻度）和圆规作出正17边形，他为此高兴异常，为了研究数学而放弃了想成为一位语言学家的强烈愿望。他不仅在数学的众多分支领域中做出了杰出的贡献，而且也实现了成为一名发明家、实验大师的愿望。尽管他的贡献在数量和深度方面丝毫不亚于其他数学家，但高斯却非常谦虚。他说：“如果其他人像我一样对数学真理进行长期深入的思考，他们也将会取得我的那些成就。”那些坚信天才是百分之九十九的勤奋但又对自己的数学能力绝望的人，也许在高斯的名言中能找到安慰。

平行线公理问题第一次引起高斯注意时，他还是一位少年。开始，他希望用一条更加简单的公理取代平行线公理而辛勤工作，然而他失败了。随后，他沿着萨凯里的思路，选择一条与欧几里得几何相矛盾的平行线公理——本质上是萨凯里的第三种选择（选择（c））——从这条公理和欧几里得的其他9条公理出发，推出了一系列结论。像萨凯里一样，他得出了许多奇怪的定理。高斯没有被这些奇怪的结论吓住，而是迎难而上。他得出了一个全新的、就是伟大的人物也想都不敢想的令人惊奇的结论。他宣称：确实能够存在类似于欧氏几何的其他几何。

高斯具有创立非欧几何的智力和勇气，但却没有精神毅力面对那些乌合之众，这群乌合之众把非欧几何的创造者称为疯子，因为19世纪早期的科学家们生活在康德的阴影之中，康德曾宣称，统治知识世界的只能是欧氏几何。正因为如此，高斯关于非欧几何的研究成果，人们在他去世后才在其论文中找到。

两位应该享受创立非欧几何荣誉的人中，第一位是富有天才的N·罗巴切夫斯基。他1793年出生于一个贫穷的俄罗斯家庭，在喀山大学学习、接受教育，23岁时成为该校教授。罗巴切夫斯基也为平行线公理问题所吸引。他说，他难以相信这样的事实：最伟大的数学家们经过2000多年的努力，居然没有创造出一条更好的公理。因此像萨凯里和高斯一样，他在与欧氏几何矛盾的平行线公理的基础上，创立了一门新的几何。那些最令人难以置信的定理，正像没有吓住高斯一样，也丝毫没有使他沮丧。这些定理是经过严密的推导而得出的，而严密的推理是无可怀疑的向导。因此，罗巴切夫斯基也宣布了革命性的但又不可回避的结论：有不同于欧几里得的几何学，其真实性与欧氏几何是一样的。

与罗巴切夫斯基分享发现非欧几何荣誉，并有勇气发表自己成果的是匈牙利人约翰·鲍耶（John Bolyai）。像高斯、罗巴切夫斯基一样，鲍耶也天赋极高，而且除此之外，他还受到了也是数学家的父亲沃尔夫罔·鲍耶（Wolfgang Bolyai）的鼓励和影响。沃尔夫罔自己为平行线公理问题伤透了脑筋，在这方面花费了多年的时间。他把自己在这方面所做的工作交给了儿子，而鲍耶在1825年年仅23岁时，突然茅塞顿开。他坚决主张，存在着与欧氏几何矛盾的能被作为新几何学基础的公理。通过与父亲进行了一番争论后，1833年在其父亲教科书的附录中，鲍耶发表了自己的观点及研究成果。

罗巴切夫斯基和鲍耶的划时代的论文是如何被人们接受的呢？科学家们对欧氏几何有了竞争对手这一爆炸性新闻的反应如何呢？极富理性的哲学家对这一完全与当时最流行的哲学背道而驰的理论作何反响呢？罗巴切夫斯基和鲍耶全然不顾这一切，而毅然决然地发表了自己的研究成果。而且，在1847年时，尽管罗巴切夫斯基在工作中做出了杰出的贡献，而且忘我地工作，但还是被大学辞退了⁽¹⁾。如果鲍耶是一位教授而不是一位奥地利（奥匈帝国）军官的话，他也可能会遭到同样的命运。

大约在罗巴切夫斯基和鲍耶发表了他们的划时代著作30年后，高斯关于非欧几何的通信在其逝世后与其他论文一同发表了。高斯的巨大声望，引起了人们对非欧几何的关注。不久，数学界开始阅读罗巴切夫斯基和鲍耶的有关著作。

为了理解他们在平行线公理问题方面的工作，现在必须回过头来再看看。考虑任意直线L（如图78）和任意不在L上的点P。欧几里得平行线公理宣称，过P有且仅有一条直线K与L不相交。现在设Q是L上的任意一点。当Q向右移动时，直线PQ就绕着P按反时针方向旋转，似乎要趋近直线K。同理，当Q沿着L向左移动时，直线PQ就围绕P按顺时针方向旋转，同样也趋近K。这样，在每一种情形下，PQ都趋近一条直线，并且是同一条极限直线K。

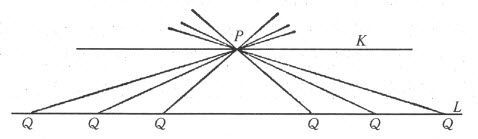
图78　作为惟一极限线的欧几里得平行线

但是，鲍耶和罗巴切夫斯基却假定PQ的两个极限位置不是同一条直线K，而是过P的两条不同的直线，而且这些极限线M和N（图79）与L不相交。他们还假定，每一条过P且在M和N之间的直线如F，都与L不相交。因此罗巴切夫斯基和鲍耶的平行线公理断言，存在无数条过P且平行于L的直线。（这些人依然用平行线一词来表示极限线M和N，但我们将利用它来代表任何过P且与L不相交的直线。）

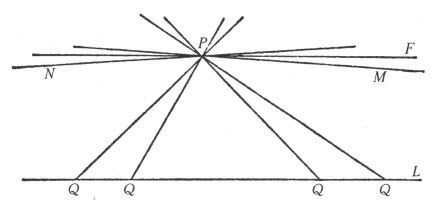
图79　罗巴切夫斯基和鲍耶的平行线公理

读者也许会像与鲍耶和罗巴切夫斯基同时代的数学家一样，觉得做这样的假设非常荒谬。图形本身就暗示出，如果M、N和L这3条直线充分延长，那么M和N必将与L相交。但是，让我们记住，鲍耶和罗巴切夫斯基的兴趣在公理的选择，而不考虑公理是否描述了我们所居住于其间的空间。从逻辑上来说，这一公理是可以选择来替换欧几里得的平行线公理的。由于从这一公理和所保留的欧氏几何的公理推导出的定理，仅仅只依赖于推理，根本不用考虑它们与图形的一致性问题，因此，公理与视觉不吻合就无关紧要了。

鲍耶和罗巴切夫斯基利用他们的公理能够说明什么呢？当然，没有利用欧氏几何平行线公理证明的所有欧氏几何中的定理，自然地也是鲍耶和罗巴切夫斯基的几何定理，因为他们保留了欧几里得的其他公理。我们可以指出这些定理有这样一些：直角相等；从点P出发，至多能向一定直线引一条垂线；以及在一个三角形中，等边对等角。

在鲍耶和罗巴切夫斯基几何中，最令人吃惊的定理的确与他们的平行线公理紧密相关，当然它们在欧氏几何中是不可能找到的。这些定理像所有的数学定理一样，是利用我们熟悉的演绎推理方法证明的；但是，与欧氏几何不同的是，图形在证明的步骤中几乎没有什么作用，图形也不能说明定理的意义。

最出人意料的定理是：任何三角形的内角和总是小于180°。而且，两个三角形中，具有较大面积的三角形，则具有较小的内角和。甚至更使人惊奇的是，新几何推翻了欧氏几何中的重要概念，即两个几何图形形状相同但它们的大小可以不同。在这样的情形下，我们就说这两个图形相似而不全等。在新的几何学中，两个相似的三角形也必定全等。我们需要提到的作为新定理的最后一个例子是：两条平行线之间的距离，沿直线的一个方向趋于零，而沿另一个方向则趋于无穷大。

利用许多令人惊奇的定理，罗巴切夫斯基和鲍耶成功地创造了一门新几何学。但是，他们的研究仅仅是一种逻辑训练吗？首先，我们认识到，新几何演绎出了数百条互相不矛盾的定理。这就意味着，原先欧氏几何中的平行线公理不能从其他欧氏公理中推导出来；否则，新几何中所作的假设将必定会在体系内导致矛盾。欧氏平行线公理不能从其他的欧氏公理中推导出来，这已不是什么新鲜事，这个事实很早以前就为人们猜到了。

鲍耶和罗巴切夫斯基的研究工作的第二个重要性，则未曾预料到。那就是，我们不能希望借助任何产生矛盾的选择，来确立欧氏平行线公理是颠扑不破的真理。因此，很清楚，早期数学家为了证明平行线公理而利用的两套体系，绝不可能都能获得成功。

但是，新几何学最伟大的意义则是完全没有预料到的。尽管逻辑训练结束了，但结论却在人们心中激起了层层波澜。有不同于欧氏几何的几何学。一位掌握这种知识的数学家，就像一个手中有气枪的小孩一样，想使用它的诱惑力太强大了，以至于忍不住要试一试。众所周知，欧氏几何精确地描述了物质空间。另一方面，鲍耶和罗巴切夫斯基的非欧氏几何，如果似乎不能描述物质空间，而且也不适合应用于物质世界——那么，它能有什么用呢？

对这个问题的最初反应，人们一般都持否定态度。如果欧氏几何是正确的，那么这门新的、与欧氏几何冲突的几何学何以也是正确的呢？而且，这些荒谬的定理如何能应用于我们熟悉的世界呢？稍微思考一下就足以表明，否定的态度太轻率了。我们有什么理由担保欧氏几何是正确的呢？确实，欧氏几何被应用了数千年，它也适合人们长期以来所形成的思维习惯。但是，让我们回顾一下欧几里得自己关心平行公理的原因。是否这种新几何所给出的是关于远离人们日常生活经验的空间区域的命题呢？空间非常巨大，而我们所能接触的区域相对来说，不过是地球表面上的一个点。我们谁知道火星表面的世界的几何，或者甚至是地球表面上空10英里的事情呢？我们根据什么断定它们必须与应用于地球上的东西相同呢？比起成百条曾经在一段日子里很有效，但最终必定还是为人们所抛弃了的科学定律来，欧氏几何不一定会比那些定律好。

正是在对这个问题进行仔细思考以后，高斯提出了一条判断欧氏几何真理性的标准。在欧氏几何中，一个三角形的内角和等于180°，而在新几何中这个内角和则小于180°。因此测量一个三角形的内角和，将判定出哪一种几何更适应物质世界。由于存在着两个原因，因而必须选择非常大的三角形。首先，在一个较小的三角形中，出现的误差将较大；第二，当三角形的形状变小时，三角形的内角和趋于180°，这正是罗巴切夫斯基和鲍耶几何中的一条定理。因为一个小三角形的内角和非常接近180°，所以测量仪器可能不能满足误差的要求。

高斯亲自进行了实验。他在3座山峰上每一处都安排了一位观测测量员。每位测量员测量他所发出的光线到另外两位测量员所形成的角度。结果测得的三角形内角和与180°相差2″。它是如此接近180°，以至于这个误差可以归结为仪器误差。因此这个实验不具判决性。

高斯三角形实验中令人头疼的地方是，即使是在最佳实验条件下，也不能证明空间是欧氏的，因为即使测量出内角之和为180°，那么由于测量时总会产生误差，因此从可能性方面来说，真正的内角之和将小于180°。实际上，实验涉及两个无根据的假设，它们中的任何一个都可能使实验中得出的结论变得不真实。第一，假设由3座山峰所形成的三角形相当大；第二，假设在三角形各边所形成的光线沿直线传播。实际上，光线可能会稍微有些弯曲，只不过是我们察觉不到而已。

我们可以将高斯的实验工作看作是一个有趣而无结果的尝试。可是，非欧几何的实用性这样一个更大的问题却依然值得我们注意。从所有试图决定两种几何哪一种更适宜于物理空间的尝试中，所得出的有趣的事实是，两者都是同样的。我们已经说明过，在新的几何学中，三角形越小，其内角和越趋近180°。如果我们利用非欧几何，并由此利用稍微小于180°的内角和，那么从实用的观点来看并无害处。同样，如果我们假设给定一点P和一条直线L，在P和L所在的平面上存在无数条过P点、平行于L的直线，这同样也没有什么害处。

我们可能认为新几何学不能应用于物质世界，因为它宣称相似三角形必定全等。画出两个真实的三角形使它们相似而不全等，这肯定是有可能的。事实上，一个三角形能够画得很大，而另一个则画得很小。但是，无论怎样仔细地画两个三角形，我们都不能断定它们是真正相似的——也就是说，它们的对应角完全相等。按照非欧几何的新观点，三角形越小，则内角和越大，只不过这种差别不易测得罢了。因此，从所有实际目的出发，我们是否接受新几何学的观点，这本身并不构成什么问题。换言之，没有什么方法能断定几何学是否能应用于物理空间；两种几何学都可以利用。我们的成见和习惯偏向于欧氏几何，这可能是因为，有时它比非欧几何更为简单。但是，这些钟爱欧氏几何的原因，并不能否认新几何学的有用性。

无疑，读者对上述说法并不满意。也许，他会对其他更令人高兴的、证明非欧几何能应用于物理世界的证据感兴趣。

现在，我们再回到欧氏几何。想像有一张很大的纸片无限地向四周延伸。这张纸片就是数学平面的一个物理解释。在平面上，欧氏几何定理成立。现在，假设我们将这片巨大的纸的左右两边弯曲，改变纸的形状，从而形成一个曲面（图80），但又继续使它像平面那样向四周无限地延伸。这样得到的曲面就是众所周知的柱面。形状改变后的结果之一是，以前平面上的直线都变成了曲线，这些曲线像平面上的直线一样，是联结曲面上两点之间的最短路径。我们称这样的曲线为短程线（geodesics）。平面上平行的两条直线成了平行的短程线，这是在曲面上两条不相交的短程线。原先平面上的三角形变成了由曲面上短程弧线所构成的图形。我们也称新的图形为“三角形”。由平面上的圆变化而产生的图形，我们也称之为“圆”。

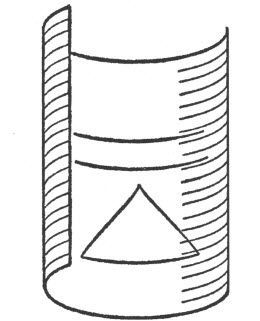
图80　欧式几何的新的图形解释

现在，我们得到了一个非常奇怪的事实。对于柱面上的图形，通过一种转换——即我们将直线、三角形、圆这些词按如上所示的方式进行解释，那么，欧氏几何中的每一条公理依然成立。因此，利用演绎法（这个过程与我们所画的图形毫不相关），从公理中推导出的欧氏几何定理，对曲面上的图形也成立。例如，曲面上的一个“三角形”的内角和也是180°。

读者可能会反对这个观点，其理由是，直线和根据直线所定义的图形，已不再具有原来的正确意义了；它们已经失去了直线的性质。现在，我们首先利用在第四章已经指出的事实，即几何中的基本概念，如点、线是不加定义的。我们仅仅利用在公理中得到详细解释的这些概念。对于某些直线的新的真实的图形，如果说直线具有公理所需要的性质，那么它就可能适应于这种新的图形。因此，把全新的真实的图像和欧氏几何的图形联系起来，在逻辑上是合理的。

刚才所给出的欧氏几何的新的物理解释，同样适应于非欧几何。如果我们的确能自由地选择直线和其他图形的物理解释，那么我们将得到一种凭直觉就可接受的新几何——非欧几何的解释。

图81所示的曲面，是众所周知的伪球面（pseudosphere），在其上面两点之间的最短路径——这些特殊的曲线也称为短程线——具有罗巴切夫斯基和鲍耶公理中直线所具有的性质。例如，两点决定着一条且只有一条直线的公理适用于这些短程线。伪球面上的两点（图81中的C，D）决定着一条且只决定着一条短程线，即两点之间最短的路径。同样，罗巴切夫斯基和鲍耶的平行公理，即过不在曲线L上的点P有无穷条线不与L相交，也适用于伪球面上的短程线。

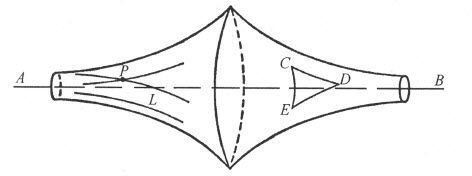
图81　罗巴切夫斯基和鲍耶的非欧几何的图形解释

因为罗巴切夫斯基和鲍耶的公理适用于伪球面上的短程线，因此作为公理的逻辑推论的定理，必定也能适用于伪球面上的短程线。由此可知，三角形内角和小于180°的定理，对于短程线所形成的三角形CDE也成立。我们仅仅只是对直线图形作了一些合理的小变化，就得到了非欧几何的一个直观解释。

对新几何做了“感官”处理之后，让我们再回到原来的问题。新几何能描述我们居住的物质世界吗？正如读者早就猜到的那样，物理空间的几何特征依赖于我们所选择的直线概念的物理意义。经验告诉我们，如果选取一绷紧的弦作为直线，则欧氏几何非常适用。但是，既没有必要也不需要让直线在所有物理应用中都代表一根绷紧的弦。现在让我们考虑一下，那些生活在山区国家的人，他们会对自己国家表面的几何学感兴趣。对他们来说，直线的最有用的物理解释就是短程线，也就是两点之间长度最短的曲线。关于这些“直线”，第一个有趣的事实是，它们随着山脉形状的不同，而从一个国家到另一个国家改变它们的形状。这些“直线”遵从什么样的公理呢？几乎肯定不会遵从任何一条欧氏公理。例如，某些地区的地形可能就是这样，在有些点对（两点）之间有几条最短的路径。通过不在一条短程线上的一个点，可以作许多条短程线，如此等等。

在天文测量中，绷紧的弦也不是直线的实际解释。在这里必须用光线取而代之。当用光线作为直线时，什么样的几何学最适用呢？我们将在下一章和读者讨论这个问题。现在，我们最好是再回到非欧几何的数学方面。我们要考查更多的数学世界。

罗巴切夫斯基和鲍耶的注意力集中在欧氏平行线公理上，但接受了欧氏几何中另一条值得怀疑的公理。即一条线段可以朝两端无限延长这一公理。在此，人们也声称这条公理描述了远离地球的遥远空间的情况。我们怎么能肯定这条公理是正确的呢，也就是说它能适用于物质世界吗？

在罗巴切夫斯基和鲍耶对平行线概念进行研究后不久，数学家锐利的目光开始注意直线的无限性，试图设法弄清这条公理的丰富内容。多病而早慧的B·黎曼（Bernhard Riemann，1826—1866），曾不得不乞求他的父亲，一位路德教的牧师，允许他放弃为谋求牧师职业而进行的训练，并使他能研究数学。被应允后，他转而开始了研究有无可能取代这条公理的工作。

他的最有价值的思想之一是，我们必须区别无界和无穷。例如，地球赤道是无界的但却是有穷的。按照这种区别，黎曼提出了取代欧氏公理中直线无穷性的一种方案，也就是提出了他的公理，即所有直线有限却无界。

这一思想立刻被用于思考平行公理问题，这与罗巴切夫斯基和鲍耶相似，但是在这种情况下导出的结果却不相同。当R沿L向左移动，Q向右移动时（图82），两个点最后必定相交，因为黎曼假设直线L是有限的。结果是，直线PR将围绕P向PQ旋转，没有一条直线不与L相交。这就是说，应该没有过P而与L平行的直线。图82不能告诉我们，按照一般的直线概念，PR绕P的旋转是何以能实现的，图示也不能更多地揭示黎曼几何的思想。这些思想对黎曼来说意味着，为了接受直线的有限性这条公理，其结果必然是不存在平行线。

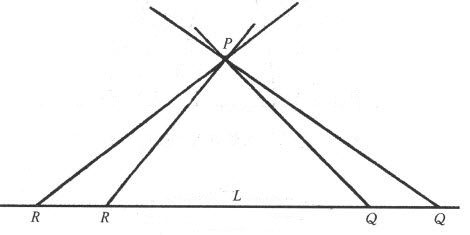
图82　黎曼平行线公理的几何基础

似乎这两点与欧氏几何的根本区别还不算太大，黎曼又提出了第三点区别：他采用了两点可以决定不止一条直线这条公理，取代了两点决定一条且仅有一条直线的公理。

在进行讨论之前，我们提请读者记住，这些公理现在被用来纯粹作为新几何逻辑发展的基础。这种相当任意的体系与现实世界两者之间的关系，随后我们将进行讨论。

黎曼几何，与罗巴切夫斯基和鲍耶几何一样，有些定理与欧氏几何是相同的。直角相等定理和一个三角形中等角对等边的定理，在3种几何中都成立，因为这些定理在3种几何中仅仅依赖于相同的公理。

黎曼几何中有些定理与欧氏几何有惊人的不同。例如：一条直线的所有垂线相交于一点（图83）。在这个奇怪的新世界中的另一个事实是，两条直线围成一个封闭的区域（图84）。因为在罗巴切夫斯基和鲍耶几何中我们发现，相似的三角形必是全等的。所以另外两条定理差不多可以猜出来：第一条定理是，任何三角形的内角和大于180°。第二条定理是，两个三角形，具有较大面积者则具有较大的内角和。

图83　一条直线的所有垂线都相交于一点

图84　两条直线围成一个封闭的区域

现在，我们可能会提出与前面讨论罗巴切夫斯基和鲍耶几何时相同的问题。除了对数学的智力训练有意义外，黎曼几何还有任何可能的意义吗？在这里，答案再一次是肯定的。利用通常理解的直线，将黎曼几何应用于物理世界是可能的，而且在几何命题与物理描述之间绝不可能会出现任何差异。在这里，论据是精确的，而且其中有一个与罗巴切夫斯基和鲍耶几何学密切相关。

通过变换直线图形，我们将发现另一个直觉上令人满意的黎曼几何解释。如同我们能在柱面上展示欧氏几何，在伪球面上展示罗巴切夫斯基和鲍耶几何一样，我们也可以在一个熟知的球面上展示黎曼几何。在一个球面上，联结两点的最短路径所形成的曲线——是通过这两点的大圆的弧。我们所指的大圆的中心也就是球心。因此，对于过A点和B点的两个圆（图85）来说，圆ABCDE是大圆，而圆ABFGH则不是。

图85　黎曼几何的图形解释

我们来看看，如果将公理中的直线解释为代表球面上的大圆弧，黎曼几何的公理是否能应用于球面上呢？首先，大圆是无界的，但长度却是有限的；其次，在球面上没有平行线，因为任何两个大圆都相交。事实上，它们不是相交一次而是相交两次。例如，大圆ABCDE和MNPD在C，D处相交。两点可以确定不止一条直线，这一公理在球面上也适合。诸如像图85中的两点N，D，不止一个大圆通过它们，而通过像A，B这样的两端就只有惟一的一个大圆。

由于黎曼几何公理正确地描述了关于球面的事实，因此利用正确的演绎推理所推导出的定理，在球面上也必定是正确的。让我们来检验几个定理。其中一个定理是，一条直线的所有垂线都相交于一点。在图86中取大圆L作为直线，我们发现L的所有垂线都相交于P点。例如，如果L是地球上的赤道，则P点将是南极或北极。

另一个定理是，一个三角形的内角和大于180°，由于公理中的直线是大圆，因此，一个三角形就是由大圆的弧所形成的图形，图86所示的ABP就是这样的三角形。由于这个三角形的两个角是直角，因此，3个内角和必定大于180°。这个事实对球面上的每一个“三角形”都是正确的。

图86　球面上的一个大圆的所有垂线都相交于一点

没有必要详谈一个已明显的观点：黎曼几何中的每一条定理，通过把定理中的直线想像为球面上的大圆，那么仅仅在球面上就能得到解释。因此对黎曼几何而言，我们能给出几何上、直觉上都令人满意的解释和意义。不仅如此，这种几何还对涉及球表面几何关系的实际的科学问题提供了标准答案。因此，在一定范围内，它肯定是物质世界的一种几何学。事实上，物质世界理论的每一条依据，如果能适用罗巴切夫斯基和鲍耶意义上的非欧几何，那么同样也可以很好地应用于黎曼几何。非欧几何对我们居住的世界的适用性，在相对论这个题目之下，将作更进一步的讨论。

回溯往事，非欧几何的创立史，就是人类的判断力不断丧失的历史。人类居住在地球表面，假定人类想建立一种几何学使之恰好适应这种地球表面，那么人们就不会认为这种特殊的表面位于三维欧氏世界之中。哪一种几何学将会得到发展呢？在这种几何学中，球面上的“直线”应该显然是联结任意两点所组成的路径为最短的曲线，因为这种曲线将是最有用的。如我们已经看到的那样，这种曲线就是连接这些点的大圆。另一方面，肯定不会选择欧氏几何意义中熟知的直线作为基本曲线，因为它在地球的表面甚至不存在。

对于这种大圆，几何学家将会选择什么公理呢？它们将正是黎曼所选择的那一套公理体系，其中不存在平行线，直线的长度将是有限的。换句话说，自然界的几何或实用的几何，在我们一般经验意义上来说，就是黎曼几何。

几千年来，这种几何一直就在人们的脚下。但是，在所有的这些年代里，最伟大的数学家从未想过试图通过检验球的几何特性而攻击平行线公理。而且作为几千年发展的顶峰，康德在欧氏几何毋庸置疑的真理观之上，建立了他深奥的哲学体系。的确，几乎不可能想像还有除欧氏几何之外其他的几何学。但是，人类却一直都生活在（如果不是住在其内的话）一个非欧几何的地球之上。

既然几何学产生于测量地球的活动，那么欧氏几何又是怎样首先发展起来的呢？答案是，人类居住在一个非常有限的区域内，地球的确看起来是平坦的，在一个平坦的表面上，最短距离的确是在一般意义下所接受的直线。利用绷紧的弦表示直线，这就自然发展出了欧氏几何的公理和定理，一旦平面几何发展起来了，球就必须纳入欧氏几何的框架内。任何人，甚至包括特别青睐球的希腊人，都没有想到通过设计一套公理去发展球的几何，以直接适用于球面。这一历史表明，人们是多么深深地被习惯思维、社会习惯（习俗）和常规束缚着。可以肯定，罗巴切夫斯基和鲍耶的先辈们之所以没有成功，并不是他们缺乏技巧，或者缺乏解决数学中困难问题的能力。他们没有解决平行线公理问题，仅仅是因为他们不能打破习惯思维——欧氏几何。这种精神停滞不前的历史，是莱基（W．E．H．Lecky）在他的《欧洲理性主义历史》（History of Rationalism in Europe）中的极好的例子，他把这一历史现象描绘为时代的精神和时代的必然性，它使得人们偏爱一种观点或信仰，而不管其论据是正确的还是错误的。因此它使得康德以及直到1800年的所有数学家都是如此。坚信欧氏几何的真理性、不可更改性和惟一性，使得任何人甚至都不可能思考另一种几何的可能性，即使非欧几何出现在他们面前时也是如此。

非欧几何的重要性，在一般思想史中没有受到重视。像哥白尼日心学说、牛顿的引力定律、达尔文的进化论一样，非欧几何对科学、哲学、宗教都产生了革命性的影响。在整个思想史中，从来没有发生过具有如此强烈影响的事件。我们这样评价，一点也不过分。

首先，非欧几何的创立，使得人们一直意识到了的，但从未认识到的一种区别变得清楚了——数学空间和物理空间两者之间的区别。由于错误的理解，致使人们最初认为两者是相同的。在我们看来，转瞬即逝的观察、视觉和触觉，都表明欧氏几何公理就是真实的物理空间，从这些公理中推导出的定理，经过视觉和触觉的进一步检验，然后它们得到了极好的验证——至少就感官所揭示的内容来说是如此。因此，欧氏几何就被当作了物理空间的精确描述。这种习惯思维在几百年中被牢固地确立起来了，因此，任何一种新几何观念都被认为是毫无意义的。几何就意味着物理空间的几何，而这种几何就是欧氏几何。但是，随着非欧几何的创立，数学家、科学家和大众最终都被迫接受这样的事实：建立在物理空间命题基础之上的思想体系与物理空间是不同的。

这种区别对于理解自1880年以来数学、科学的发展是至关重要的。我们必须强调的是，一种数学空间显示了一种科学理论的本质。因此，只有当它适合于经验的事实和满足科学需要时，才能被应用于物理空间的研究。但是，如果一种数学空间能够为一种在扩充了的科学范围内更接近论据的另一种空间所取代，那么它必然被取代，就如同托勒玫天体运动理论被哥白尼理论取代一样。如果读者发现这种可能性在他阅读下一章时已被证实，那么将不应该感到惊奇。

因此，我们应该把任何关于物理空间的理论都看作是一种纯粹的主观构造，而不要责备它与现实相悖。人创造出一种几何，欧氏几何或非欧几何，然后由此决定其空间观。这样的好处是，尽管不能肯定空间具有在自己思想创造的结构中的任何特征，但却能对空间进行思考，并且在科学研究中利用这一理论。这种空间观、自然观一般并不否认诸如物质世界这样的内容，它仅仅强调了这样的事实：人们关于空间的判断、所获得的结论，纯粹是自己的创造。

非欧几何的创立扫荡了整个真理王国。在古代社会，像宗教一样，数学在西方思想中居于神圣不可侵犯的位置。数学庙堂中汇集了所有真理，欧几里得是庙堂中最高的神父。但是，通过鲍耶、罗巴切夫斯基、黎曼，这3个为神所不容的“邪恶之人”的研究工作，却摧毁了狂热的宗教徒、最高的神父和所有信教者所信奉的神圣的宗教法令。的确，这些勇敢的有识之士在他们的研究中，只关心由新的平行线公理推导出的结论的逻辑问题。开始时，他们肯定还没有对真理本身进行挑战。一旦他们的工作被认为仅仅是一场灵巧的数学骗局，那么将不会导致严肃的问题。但是，当人们认识到非欧几何可能真实地描述了物理空间时，它本身就成了不可回避的事实。一向宣称是描述关于数量和空间真理的数学，现在怎么出现了几种相互矛盾的几何学呢？这些几何学中，只有一种可能是正确的。的确，甚至更使人心烦的是，也许所有不同的几何学都是正确的。因此，新几何学的创立迫使人们认识到这样的事实：所有的几何学都可能是一种关于数学公理的“假设”，假设欧氏几何的公理是关于物质世界的真理，那么其定理也是。然而，遗憾的是，我们不能先天地决定欧氏几何的公理——或者任何其他几何的公理——是真理。

在数学丧失了作为真理总汇的地位以后，非欧几何的创立使人们丧失了对真理的极大的尊重，甚至丧失了对任何事物具有确定性的希望。1800年代以前，每个时代都坚信存在着绝对真理；真理的差异仅仅是，由于人们所选择的绝对真理的源泉不同而已。亚里士多德，这位基督教、《圣经》、哲学和科学之父，在那些年代里总是被当作是客观的、永恒的真理的主宰者。在18世纪只有人的理性是确定的，这是由于它在数学和在科学的数学领域所产生的作用。拥有数学真理一直特别令人满意，因为它揭示出更多的希望将会到来。现在，希望破灭了！欧氏几何统治的终结，就是所有绝对标准统治的终结。哲学家可能依然宣称坚信深刻的思想的真理性；艺术家可能深情地坚持认为，他们的专门技巧使得理解真理成为再明显不过的事实；神学家可能觉得，雄伟的教堂充满着神的回音；而浪漫派诗人也许在使我们的有识之士昏昏入睡之后，再使人们不加批判地接受他那迷人的诗篇。也许，这些都是真理的源泉。也许还有另外其他的源泉。但是，吸取了非欧几何教训的富有理性的人，至少会小心防范以免落入陷阱。即使他接受任何真理，除了时刻警惕之外，他的确还会如此这般的进行试验。令人不解的是，尽管新几何学对人类获得真理的能力提出了非难，但它们却提供了人类思想具有无穷力量的最好实例。因为为了建立这些几何学，思想必须摧毁和战胜习惯、直觉和感觉。

真理神圣性的丧失，似乎解决了关于数学自身本质这一个古老问题。数学是像高山、大海一样独立于人而存在，还是完全是人的创造物呢？换句话说，数学究竟是数学家们经过辛勤劳动挖掘出的深藏了若干世纪的宝玉，还是他们制作出的一块人造石头呢？甚至在19世纪后半叶，非欧几何已经为人们所知晓的情况下，卓越的物理学家H·赫兹还说道：“人们不能不感到惊奇，这些数学公式独立地存在着，而又具有自己的智慧，它们比我们更聪明，甚至比这些公式的发现者更聪明。从这些公式中我们得到的，比开始注入到其中的更多。”尽管有这种观点，但数学的确似乎是人造的、易犯错误的思想的产物，而不是独立于人的永恒世界中的东西。数学并不是建立在客观现实基础上的一座钢筋结构，而是人在思想领域中进行特别探索时，与人的玄想连在一起的蜘蛛网。

如果说非欧几何的创立，粗暴地使数学丧失了真理性基础，那么另一方面它也使数学获得了自由发展的境地。实际上，罗巴切夫斯基、黎曼和鲍耶的工作，给予了数学家们自由处理他们所需要的无论怎么奇怪的内容的权力。因为非欧几何最初的目的，就是为了研究有趣的逻辑严密性的问题，这被证明具有无可比拟的重要性。现在，这一点似乎已经很清楚了，数学家应该探索任何可能的问题，探索任何可能的公理体系，只要这种研究具有一定的意义；运用于现实世界的这一数学研究的主要动力，依然为人们所遵从。数学史上的这一阶段，使得数学摆脱了与现实的紧密联系，使数学自身从科学中分离出来了，就如同科学从哲学中分离出来，哲学从宗教中分离出来，宗教从万物有灵论和迷信中分离出来一样。现在，可以使用G·康托尔的话了：“数学的本质就在于它的充分自由。1830年以前，数学家的处境可以比作是一位非常热爱纯艺术，而又不得不接受为杂志绘制封面的艺术家。从这种限制中解脱后，艺术家就可以无限制地发挥他的想像力和创造力，创造出众多的作品。非欧几何正是这种解脱的因素。”19世纪中叶以来，数学活动的大量扩张，以及在数学家的工作中更加强调美学作用，就是新几何学影响的例证。

非欧几何在思想史上所具有的无可比拟的重要性，就是使2000多年来有关“无用”的逻辑问题发展到了顶峰。这样，数学提供了一个不受实用性左右，而是受抽象思想和逻辑思维支配的范例，并且也是灵机一动的智慧摒弃感觉经验的范例。这就如同哥白尼要求我们对待他的日心学说一样，因为这种学说也是人类思想的创造物。

 

————————————————————

(1) M·克莱因在这里太夸张了。罗巴切夫斯基一直在喀山大学及全俄国很受重视，并于1827—1846年担任了长达20年的喀山大学校长。只是于1846年辞去校长职务后，改任喀山学区副督学，使他有一种失落感。——译者注