分析线性电路暂态过程的复频域法

用拉普拉斯变换分析线性动态电路暂态过程时，首先要按7.4节所述原则把电路的时域模型变换为复频域模型或运算模型，然后根据复频域的电路定律和元件特性建立电路方程。这些电路方程其实就是分析电阻电路的代数方程和分析正弦稳态电路的相量方程的推广。可沿用以前介绍的各种方法，在复频域内求出电路中的电流或电压的象函数，这些象函数一般都是有理真分式，可用部分分式法展开成简单的部分分式，从表7-1中查出其原函数。采用这种方法，不必从建立电路的微分方程开始，而且电路的原始状态值的影响已用附加电压源加以考虑了，无需确定积分常数，这是该法一大优点。现把它的具体步骤概括如下：

（1）确定电感的原始电流iL（0-）和电容的原始电压uc（0- ）。

（2）求出已知激励电压源和电流源的象函数。

（3）画出电路的复频域模型。

（4）应用计算线性电阻电路的任何一种方法（如串并联化简、支路电流法、回路电流法、节点电压法、叠加定理、戴维南定理等）解电路的复频域模型，求出待求变量的象函数。

（5）利用部分分式法及拉普拉斯变换表，将象函数变成原函数。

例7-9　图7-6（a）所示为RC串联电路，求其单位阶跃响应和单位冲激响应（电容电压）。

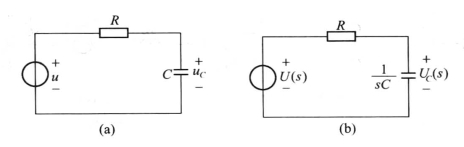
图7-6　例7-9图

解　作出图7-6（a）所示电路的复频域模型，如7-6（b）所示。

（1）当时，则

由部分分式法，有

则电路的单位阶跃响应s（t）= uc（t），即

（2）当U（s）=L［δ（t）］=1时，则

电路的单位冲激响应h（t）=uc（t），即

例7-10　已知图7-7（a）所示电路中R1=6Ω， R2 =3Ω， C1 =1F， C2 =3F，外施激励电压为us（t）=12ε（t）V，已知电容原始储能为零，求u0（t）。

图7-7　例7-10图

解　（1）作电路的复频域模型，如图7-7（b）所示。由于电容原始储能为零，故无附加电源。外施激励电压源的象函数为

（2）电路中复频域阻抗

电压u 0（t）的象函数U0（s）为

例7-11　图7-8（a）所示电路中，Us =200V，R=20Ω，L=0.1H，C=1000μF，电容原始电压uc（0-）=100V，极性如图所示。t=0闭合开关，求电流i1（t）。

图7-8　例7-11图

解　（1）作出电路的复频域模型，如图7-8（b）所示。其中

（2）应用回路电流法，得

代入数据，则得

解得

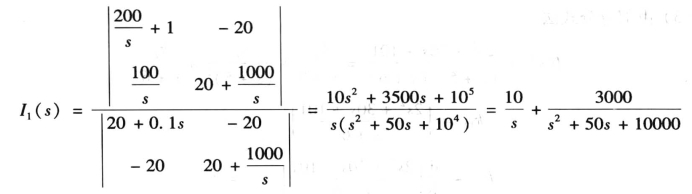
（3）应用部分分式法把I1（s）分解成部分分式，令

例7-12　图7-9（a）所示电路中，原始状态值iL（0-）=0，uc（0-）=4V，试求电流i（t）。

图7-9　例7-12图

解　（1）作出电路的复频域模型，如图7-9（b）所示。

（2）应用弥尔曼公式，得

（3）由部分分式法

图7-10　例7-13图

解　（1）由于换路前电路已处于稳态，所以

（2）作出电路的复频域模型，如图7-10（b）所示。

（3）应用弥尔曼公式，得

（4） （t） （t）和（t）为

此题属于强迫跃变的类型题。在t=0-到0+期间（t）由（0-）= 10V跃变为（0+ ）=4V，（t）由（0-）=0跃变为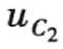（0+）=4V，电容电流出现冲击电流分量。