节点分析法

对于具有n个节点和b条支路的网络，任选一个节点作参考点，写出其关联矩阵A，则用矩阵A表示的KCL和KVL的复频域形式为

再根据式（8-12）写出用支路导纳矩阵表示的支路VCR方程

则以上三式是推出网络节点方程的依据。

将支路VCR方程代入KCL方程，得

再将KVL方程代入上式，整理则得

式（8-17）就是矩阵形式的节点方程。

则式（8-17）简化为

式中：In（s）称为节点源电流列向量，它的每个元素表示流入相应节点的各源电流（包括等效电流源）的代数和；（ns）称为节点导纳矩阵。

由式（8-20）解出节点电压列向量Un（s）后，不难求支路电压和支路电流列向量

这就是节点分析法。

例8-3　列出图8-13（a）所示网络的节点电压方程，已知网络处于零原始状态。

图8-13　例8-3图

解　（1）作出网络的复频域模型和有向图，如图8-13（b）、（c）所示。

（2）选节点④为参考点，写出关联矩阵A

（3）写出网络的支路导纳矩阵Yb，按式（8-18）计算出节点导纳矩阵Yn（s）

由式（8-18）得

（4）写出电源列向量Us （s）和Is（s），按式（8-19）计算出节点电流源列向量In（s）

则由式（8-19）得

（5）写出矩阵形式的节点方程

对图8-13（a）所示的不含耦合元件的网络，其矩阵形式的节点方程可用观察法直接写出：按第2章的节点分析法对图8-13（b）所示网络列出节点方程，并表示成矩阵形式，则得上面相同的结果。读者可自行验证。

对于直流电阻网络，式（8-17）～式（8-20）变为

式中：Gn称为节点电导矩阵。

对于正弦电流电路，式（8-17）～式（8-20）变为

例8-4　写出图8-14（a）所示正弦电流电路的节点方程。

图8-14　例8-4图

解　（1）画出给定电路的拓扑图，标出支路的参考方向，如图8-14（b）所示。

（2）选节点④为参考点，写出关联矩阵A

（3）写出支路阻抗矩阵Zb（jω），计算支路导纳矩阵Yb（jω）和节点导纳矩阵Yn（jω）

则

（4）写出电源列向量is，计算节点电流列向量in

则

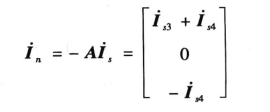
（5）节点电压方程为

具有受控源的网络，其节点电压方程的列写本书不加讨论，读者可参阅其他参考书。