二端口网络的导纳矩阵和阻抗矩阵

1.短路导纳矩阵

图9-3　二端口的端电压用电压源替代

可见，Y11（s）是表示端口2短路时，端口1的输入导纳，也称端口1的策动点导纳；而Y21（s）是表示端口2短路时，端口2与端口1间的转移导纳。

同理，在端口2外施电压源U2（ s），而将端口1短路，即U1（s）=0，如图9-4（b）所示。由式（9-1）可得

图9-4　短路导纳的测定

可见，Y1（2 s）是表示端口1短路时，端口1与端口2间的转移导纳；而（s）表示的是端口1短路时端口2的策动点导纳。

由于Y参数都是在一个端口短路情况下通过计算或测试而求得的，因此也称为短路导纳参数。式（9-1）则称为短路导纳参数表示的二端口网络方程。

将式（9-1）表示成矩阵形式

令

式中：Y（s）称为二端口网络的短路导纳矩阵。

例9-1　求图9-5（a）所示二端口网络的Y参数。

解　将端口2短路，端口1加电压源U1（s），如图9-5（b）所示。则端口1的电流为

端口1的策动点导纳为

端口2的电流为

端口2与端口1间的转移导纳为

同理，将端口1短路，端口2加电压源U2（s），如图9-5（c）所示。则可得端口2的策动点导纳为

图9-5　例9-1图

端口1与端口2间的转移导纳为

所以短路导纳矩阵为

从例9-1可以看到短路导纳矩阵是对称的，即Y12（s）=Y21（s）。由8.12节知，由线性R、L、C、M元件组成的无源二端口网络是互易的，因此有Y12（s）=Y21（s）；反之，若二端口网络满足（s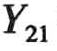）=（s），则此二端口网络是互易的。含有受控源的二端口网络一般是非互易的。互易的二端口网络，Y参数仅有3个是独立的；非互易的二端口网络，Y参数的4个参数都是独立的。

例9-2　求图9-6（a）所示二端口网络的Y参数。

图9-6　例9-2图

解　此二端口网络与例9-1的二端口网络相比较，Y11 （s） 、Y12（s） 、（2s）是相同的，仅Y21（s）不同。当端口2短路，端口1加电压源U1（s）时，如图9-6（b）所示，则

所以

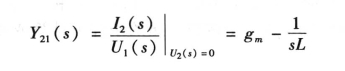
网络的短路导纳矩阵为

此二端口网络是非互易的，（s）≠（s）。

2.开路阻抗矩阵

Z11（s）、Z12（s） 、Z21（s） 、Z22（s）称为阻抗参数，也称为Z参数。这4个参数可按下述方法计算或实验测量求得：假定端口2开路，即I2（s）=0，在端口1上施加电流源I1（s），如图9-7（b）所示。由式（9-7）得

Z11（s）称为端口2开路时端口1的策动点阻抗；Z21（s）称为端口2开路时端口2与端口1间的转移阻抗。

图9-7　开路阻抗参数的测定

同理，将端口1开路，即I1 （s）=0，端口2施加电流源I2（s），如图9-7（b）所示。由式（9-7）得

式中（2s）称为端口1开路时端口2的策动点阻抗；Z12（s）称为端口1开路时端口1与端口2间的转移阻抗。因为Z参数都是在一个端口开路的条件下计算或测试得到的，所以也称为开路阻抗参数。

对互易网络，有Z12（s）=Z21（s），所以互易二端口网络只有3个独立的参数。对称的二端口网络，除了Z12（s）=Z21（s）外，还有Z11（s）=Z22（s）。

把式（9-7）写成矩阵形式，则有

式中

Z（s）称为开路阻抗矩阵。

比较式（9-6）和式（9-10），开路阻抗矩阵Z（s）与短路导纳矩阵Y（s）只要是非奇异的，则它们互为逆阵，即

式中△Y=Y11（s）（2s）-Y12（s）Y21（s）。

对给定结构的网络，有的并不同时存在开路阻抗矩阵和短路导纳矩阵。对图9-8（a）所示二端口网络，短路导纳矩阵为

图9-8　串臂导纳和并臂阻抗组成的二端口网络

由于△Y =0，Y（s）不存在逆阵，故无开路阻抗矩阵。对图9-8（b）所示二端口网络，其开路阻抗矩阵为

由△z =Z11（s）Z22（s）-Z12（s）Z21（s） =0，Z（s）不存在逆阵，故无短路导纳矩阵。

当然，有的二端口网络既不存在开路阻抗矩阵，也不存在短路导纳矩阵，如前面讲到的理想变压器。