量子力学的魅力

鉴于量子力学的基本算符是不对易的，要将一个算符函数排列为某种有序，就需一番功夫。对于同一算符函数，不同的算符排序会出现不同的特殊函数。

经典物理中相空间是以质点的坐标q与动量p的坐标构建而成的，过渡到量子论中，受海森堡的不确定性原理的限制，人们不能同时精确地观测粒子的位置与动量，即不能确定到一个相点，而至多只能确定到一个面积为ћ/2的小圆，它对应相干态。另一方面，经典函数f（q，p）的不同量子化方案也造就了其在量子相空间中的不同“图案”。

以经典相空间中的一条射线为例，来说明不同的量子化方案相应于量子相空间中不同的量子“图案”对应。经典相空间中的一条射线方程是x－λq－νp=0（这里λ与ν是实参数），它以(x－λq－νp)表示。我们的研究结果发现，仅当取Weyl量子化，经典相空间中的一条射线在量子相空间的“图案”对应为射线，而在其他量子化时，如Q－P排序量子化（所有的坐标算符Q排在所有的动量算符P的左边）以及P－Q排序量子化（所有的动量算符P排在所有的坐标算符Q的左边），射线映射几何图形为椭圆。

在量子力学中，由于坐标算符与动量算符不对易[Q，P]=i（这里ћ=1），所以把一个经典函数f（p，q）量子化为算符时，会给出不同的结果，最简单的例子是经典函数p^mqⁿ有多种不同的量子对应，其中两个是QⁿP^m或P^mQⁿ，如选QⁿP^m，则根据坐标表象与动量表象的完备性

就有

所以

于是（2）式变为

把一个单项里的所有Q置于所有P的左边，记为－排序，上式是qⁿp^m的－排序量子化方案。另一方面，如选量子化为qⁿp^m→P^mQⁿ，根据（1）就有

可见积分核是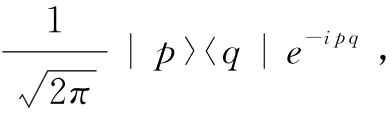，鉴于

（6）式变为

这里P置于Q左边，这是qⁿp^m的P－Q排序量子化方案。可见，量子化qⁿp^m的结果取决于在选方案时用Q－P排序（Q置于P左边）方案还是用排序（P置于Q左边）方案。注意，以上的讨论建立在（1）式的基础上，反映了坐标表象与动量表象的新应用。而（5）和（8）式的右边都体现了有序算符内积分的思想。

而其－量子化是

这里用了Baker-Hausdorff公式。如取另一种量子化方案，是使得经典函数e^iqu+ipυ正好量子化为e^iQu+iPυ，

我们称它为Weyl量子化，也就是要找一个积分核Δ(p，q)（称为Wigner算符），使得

从此式我们看出两点结论：

所以Δ(q，p)本身的Weyl排序是

（2）把（13）看做是Fourier变换，所以其反变换给出

进一步将Δ(q，p)排成－排序积分，得到

可见，Δ(q，p)与δ(p－P)δ(q－Q)存在如下的变换关系

类似可得Δ(q，p)与δ(q－Q)δ(p－P)的变换关系

注意在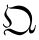编序的记号内，P与Q也是可交换的。可以证明（17）式的反变换是

经典函数δ(x－λq－νp)的－排序、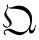－排序以及Weyl排序量子化方案

现在我们讨论经典函数δ(x－λq－νp)的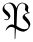－排序、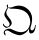－排序以及Weyl排序量子化方案。

（1）δ(x－λq－νp)的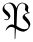－排序量子化方案，积分核是δ(p－P)δ(q－Q)，故有

注意，在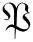编序的记号内，P与Q也是可交换的。我们可以进一步求出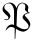δ(x－λQ－ΔP)的Weyl排序形式

非常需要注意的是：从最右边的Delta函数中看不出P在Q前，所以我们必须以下面的方式继续：

其中的指数算符是Weyl排序了的，所以

（2）δ(x－λq－νp)的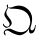－排序量子化方案。

积分核是δ(q－Q)δ(p－P)，

求出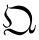(x－λQ－νp)的Weyl排序形式，得

（3）δ(x－λq－νp)的Weyl排序的量子化方案。

积分核是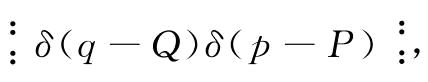根据（14）可以直接得到

比较（23）、（25）和（26）可见，对于同一个δ(x－λq－νp)，其三种量子化方案给出的几何图形截然不同。