顺水而走的石头

河水在冲刷河岸的过程中，不仅能将河底的泥沙碎块带到河床边，就连河底的石头也能推走。河底的石头往往块头很大，水是怎么把它们带走的呢？当然，要施展这个“威力”也要看是哪条河里的水，不是所有的河水都有这个力气的。平原上的河水流速慢，最多不过是带走一些细沙。不过，只要水的流速增加，河水的能力就会大很多。如果河水的流速增加到一倍那么多，就可以把大块的卵石带走了。山涧的急流流速又要增加一倍（见图76），冲走大于1000克的大石头也不是问题，怎样解释这个现象呢？

图76　山涧急流使石块滚动

流体力学中有一个“艾里定律”，这个定律可以证明，当水的流速增加n倍时，水流可带动的物体的重量就会增加到n6倍。

自然界中罕见的六次方比例出现在这里，不免让人觉得好奇，这个比例是怎么来的呢？

我们假设河底有一块边长为a的立方体石块（见图77）。河水流动过程中，水流的压力F作用于石块侧面S，想要使石块以边AB为轴向前滚。但与此同时，石块在水中的重力P向它施加了反作用，阻碍石块做翻转运动。水流与石块陷入了僵持状态，石块怎样才能被水流成功翻转呢？根据力学定律，当力P与力F对轴AB的力矩相等时，石块才能保持平衡。某个力和它本身与轴之间的距离的积就是力对轴的力矩，力F的力矩是Fb，力P的力矩就是Pc。由于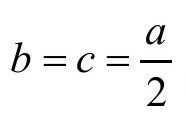，所以只有当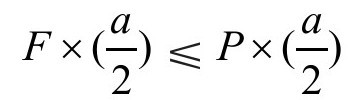的时候，或者说当F≤P的时候，石块才能保持平衡。接下来我们要使用公式Ft=mv，其中力作用的时间为t, t秒钟内作用于石块的水的质量为m，水流的速度为v。

图77　石块在水流中受到的作用力

根据流体动力学的定律，水流施加于与水流方向垂直的平面上的总压力与平面面积成正比，与水流速度的平方成反比。用公式表示为：。从石块的体积a3与其比重d的乘积中减掉同样体积的水的重量，就等于石块在水中的重量（阿基米德定律），用公式表示为：

因此可以将F≤P变换为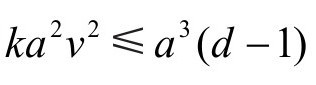，可推出。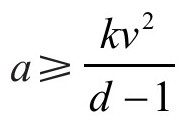

我们知道，能与速度为v的水流抗衡的石块，它的边长要与水流速度的二次方成正比，而石块的重量与它的边长a的三次方成正比即。六次方就是这样出现的，被水流冲走的石块的重量与水流速度的六次方成正比。

这就是艾里定律，我们借助于一块正方体的石头证明了这一定律。不过这并不能说明只有借助立方体才能做这个证明，其实用别的形状的物体证明也是一样的，最终的结论之间差别不大，并且每种结果都足以说明问题，而现代流体力学还有很多更加有说服力的论证。