生存分析可以广义地认为是对生存时间(非负随机变量)的一类统计分析技术[1].生存时间常用来表示自然界、人类社会或技术过程某种状态的持续时间.一种最常见的情况是,用生存时间表示“寿命”(技术产品的寿命或生物、人的寿命),因而生存分析可看成是对寿命进行研究,是对寿命数据进行分析.生存分析对产品寿命的评估、人和生物寿命的研究、手术后人的寿命预测等等都是十分重要的,因而生存分析的理论和方法在工程、医学及生物学上都有广泛的应用价值,日益受到人们的重视.
生存分析不是孤立地研究某个个体的生存时间,而是研究一批个体的生存时间.任何个体的寿命带有偶然性,而一批个体的生存时间多长就有一定的规律性.生存时间可以广泛地定义为一给定的事件发生的时间.这个事件可以是疾病的发生、一种治疗(处理)的反应、疾病复发或死亡.因此,生存时间可以是无肿瘤时间,从一种治疗开始到有反应的时间,缓解时间长度或出现死亡的时间.生存数据可以包括生存时间、对治疗的反应、与生存和疾病发生有关的患者特征.生存数据不仅出现在生物医学中,而且出现在可靠性工程、社会科学和商业研究中.在这些领域生存数据的例子有:可靠性工程中电子设备、元件或系统的寿命,犯罪学中重罪犯人的假释时间,社会学中首次婚姻的持续时间.生存时间也可以不是时间,它可以是汽车车轮的圈数,也可以是市场学中报纸或杂志的篇幅和订费,甚至可能是保险公司在某一索赔案中所付的保险费等.我们用表示任何个体的生存时间,把T看成随机变量,T的分布依赖于个体.
1.随机变量T的特征通常用下面3个函数来刻画
(1)生存函数.生存时间T的生存函数用S(t)=P(T>t)来表示,它实际上是个体生存时间长于t的概率.在工程上常用记号R(t)代替S(t),称之为可靠性函数,若t0是完成任务所需要的任务时间,则R(t0)就是可靠度.生存函数是生存分析中最基本的特征函数,它在生存分析中的地位相当于总体的分布函数.生存函数S(t)也叫累积生存率,它的图形叫做生存曲线.陡峭的生存曲线表示低的生存概率;较平坦的曲线表示高的生存概率.
(2)概率密度函数.在实际工作中遇到的生存时间大多是连续的,即T有概率密度函数f(t)=[1-S(t)]′.
概率密度函数的统计问题无论在应用统计还是理论统计中都有非常重要的作用,特别是估计概率密度函数的非参数方法在决定一个总体的统计特征时是很重要的.
(3)风险率函数.风险率函数是刻画生存时间的重要特征之一,它实际上是条件生存率,设λ(t)表示风险率函数,则其定义可用以下公式表示:
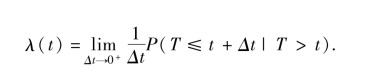
从以上定义可知,λ(t)是在时间t仍然活着的个体,在接下来的单位时间区间内死亡的条件概率.当生存时间T的概率密度函数f(t)存在时,λ(t)又可通过下面公式来定义:

风险率函数在可靠性统计中又称为失效率函数,而在生存分析及医学研究中也叫危险率函数、瞬间死亡率、死亡强度、年龄死亡率及条件死亡率等.这个函数用于测量一定年龄的个体是否容易死亡,而Δtλ(t)是年龄为t的人在较短的时间区间(t,t+Δt)中死亡的比例,因此风险率函数给出了年龄增长过程中单位时间内的死亡风险,这个函数在生存数据分析中起重要的作用.
2.刻画T的主要特征数
(1)平均寿命μ:
为T的数学期望.
(2)寿命方差σ2:
![]()
为T的方差.
(3)分位寿命ξp:
![]()
为T分布的上p分位数.特别地,当p=0.5时,
![]()
为T分布的上中位寿命.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















