令X(i)j,i=1,2,…,m;j=1,2,…,k为抽自T的均衡排序集样本;Tij,i=1,2,…,m;j=1,2,…,k是非负独立同分布表示删失的随机变量,具有分布函数G.在随机右删失模型下,我们不能完全观察到X(i)j,而仅能观察到

因此,我们得到删失排序集数据对
![]()
问题为如何由这些数据对估计生存函数S(t).
Kaplan&Meier(1958)[132]提出了删失简单随机样本的乘积限估计,此估计方法是生存数据分析中最广泛使用的方法.借助下删失简单随机样本的乘积限估计量构造的思想,我们可以构造出删失简单随机样本的乘积限估计.
设Y(1:1)≤Y(2:2)≤…≤Y(n:n)是Y(i)j,i=1,2,…,m;j=1,2,…,k的从小到大的次序值,如果删失观察与非删失观察有相同的值,则后者应排在前面.
令δ(i:j)为相应于Y(i:j)的δ,即当Y(l:n)=Y(i)j时,
设 (t)记在时间t的风险集,即在时刻t之前仍然活着的个体数,且设
(t)记在时间t的风险集,即在时刻t之前仍然活着的个体数,且设
r(i:n)= (Y(i:n))中的个体数,
(Y(i:n))中的个体数,
d(i:n)=在时刻Y(i:n)之前死亡的人数,
p(i:n)=P(生存时间超过Y(i:n)|生存时间超过Y(i-1:n))
=P(T>Y(i:n)|T>Y(i-1:n)),
q(i:n)=1-p(i:n).
显然,q(i:n)与p(i:n)可以如下估计得
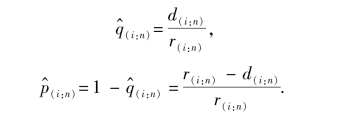
这样,删失排序集抽样(CRSS)下生存函数的直接乘积限估计为
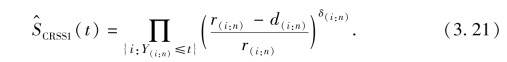
如果最大观测值Y(n:n)是删失的,那么规定当t≥Y(n:n)时

显然,当所有观测值都是非删失数据时,公式(3.21)就是生存函数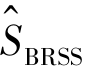 (t).特别地,在观察没有“结”时,
(t).特别地,在观察没有“结”时,
r(i:n)=n-i+1,
且
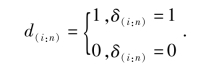
此时,
因为当Y(i:n)为删失观测值时,δ(i:n)=0,所以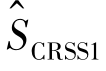 仅需求考虑非删失观测值,若令
仅需求考虑非删失观测值,若令
![]()
为Y(i)j,i=1,2,…,m;j=1,2,…,k中所有非删失观察值从小到大的次序值,且设
 =在时刻
=在时刻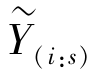 之前死亡的人数,i=1,2,…,s,
之前死亡的人数,i=1,2,…,s,
其中s为所有非删失观察的个数,则公式(3.21)也可表达为
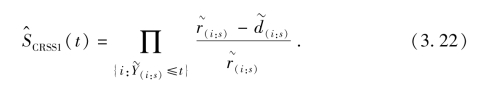
这样,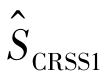 (t)可以按下式计算
(t)可以按下式计算
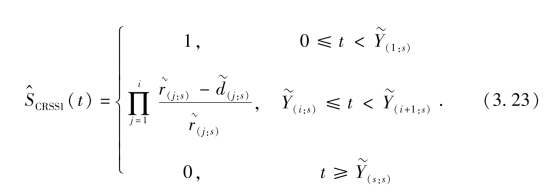
实际中,公式(3.23)可以通过一个6列的表计算,计算过程为:
(1)第一列按从小到大的顺序列出全部非删失观察的生存时间.
(2)第二列i,是非删失观察在包括删失和非删失全部观察中所对应的秩.
(4)第4列标号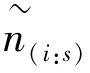 ,是对应在第一列非删失观察时刻之前仍然活着的个体数.
,是对应在第一列非删失观察时刻之前仍然活着的个体数.
(5)第5列对应每一个非删失观察,计算
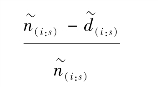
(6)第6列对应每一个非删失观察,计算
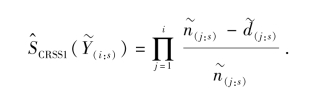
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















