典型环节频率特性

1）放大环节

放大环节的频率特性式分别有

放大环节幅频是常数K，相频特性是0°，均与频率无关。

图5-10所示为放大环节的Nyuist图，是实轴上的一个点，增大K，此点向正方向移动。

图5-10 放大环节的Nyuist图

图5-11 放大环节Bode图（G（jω）＝100）

图5-11所示为放大环节的Bode图。幅频曲线为20lgK（d B）的一条水平直线，K＞1时在零分贝线以上，K＜1时在零分贝线以下。相频曲线为一零相位水平直线。

一般系统增大K使幅频曲线向上移动，减小K使幅频曲线向下移动，但幅频形状不变。增益变化不影响相频特性故相频曲线无变化。故讨论其他环节的Bode图时往往假设K＝1。

2）积分环节

积分环节的频率特性式分别有

放大环节幅频随ω增加而减小，相频特性为常数－90°与频率无关。

图5-12所示为积分环节的Nyuist图，是一条与负虚轴相重合的直线。

图5-12 积分环节的Nyuist图

图5-13 积分环节Bode图

图5-13所示为积分环节的Bode图。幅频曲线为一条斜率为－20d B／dec直线且与零分贝线相交于ω＝1，即

L（ω）∣ω＝1＝－20lgω∣ω＝1＝0

相频曲线为－90°的水平直线。

3）纯微分环节

纯微分环节的频率特性式分别有

纯微分环节幅频随ω增加而增大，相频特性为常数90°与频率无关。

图5-14所示为纯微分环节的Nyuist图，是一条与正虚轴相重合的直线。

图5-14 纯微分环节的Nyuist图

图5-15 纯微分环节Bode图

图5-15所示为纯微分环节的Bode图。幅频曲线为一条斜率为＋20d B／dec的直线且与零分贝线相交于ω＝1。相频曲线为－90°的水平直线。

4）惯性环节

惯性环节的频率特性式分别有

可知

当ω＝0时，G（j0）＝1∠0°＝1＋j0，φ（ω）＝0°；

当ω＝∞时，G（j∞）＝0∠－90°＝0＋j0，φ（ω）＝－90°。

图5-16所示为惯性环节的Nyuist图。当频率ω由0变化到∞时，惯性环节的幅相频率特性是以（0．5，j0）为圆心，半径为0．5的一个半圆，即圆方程为

图5-17所示为惯性环节的Bode图。幅频曲线可近似地用两条渐近线（图5-17中虚线）来表示。

（1）低频段是一个幅值等于0d B的水平线；

图5-16 惯性环节的Nyuist图

（2）高频段，是一条斜率为－20d B／dec的直线。

两条渐近线相交之处的频率ω＝，称为转折频率。

初步设计阶段可利用渐近线画出的Bode图。由图5-17知由于采用渐近线而在幅值上产生的最大误差发生在转折频率ω＝处，并近似为

同样可知在低于或高于转折频率一倍频程处误差均为－1d B；在低于或高于转折频率十倍频程处的误差近似等于－0．04d B。因此可以对渐近线进行修正以得到较精确的频率特性曲线：在转折频率处画一个低于渐近线3d B的点，在低于或高于转折频率一倍频程处画一个低于渐近线1d B的点，然后以一条光滑曲线连起来。

惯性环节的Bode图中相频为负反正切函数，在转折频率处斜对称，并有－45°。

5）一阶微分环节

一阶微分环节的频率特性式分别有

G（jω）＝jτω＋1

图5-18所示为一阶微分环节的Nyuist图，只是将纯微分环节的幅相频率特性曲线右移1。

图5-18 一阶微分环节的Nyuist图

图5-19 一阶微分环节Bode图（G（jω）＝1＋j100ω）

图5-19所示为一阶微分环节的Bode图。一阶微分环节与惯性环节只相差一个符号。故幅频图中在ω＜时是一条零分贝线；在ω＞时是一条斜率为＋20d B／dec的直线，交点处的转折频率为ω＝。相频为反正切函数，在转折频率处斜对称，并

6）振荡环节

振荡环节的频率特性式分别有

可知

（1）ω＝0时，G（jω）＝1∠0°，φ（ω）＝0°；

（2）ω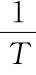＝时，G（jω）＝，φ（ω）＝－90°；

（3）ω＝∞时，G（jω）＝1∠－180°，φ（ω）＝－180°。

图5-20所示为振荡环节的Nyuist图，从1∠0°开始到0∠180°结束并与负实轴相切。与负虚轴相交点的频率为无阻尼自然频率ωn。

振荡环节的幅频和相频不仅与ω有关，还与阻尼比ζ有关。图5-21即为具有不同ζ值时的振荡环节Bode图。暂不考虑ζ，有

（1）低频段，是零分贝的水平线；

（2）高频段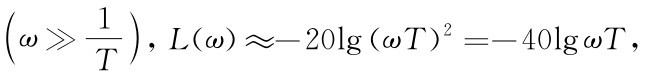是一条斜率为－40d B／dec的直线。

图5-20 振荡环节的Nyuist图

两条渐近线相交于ω＝＝ωn，无阻尼自然频率ωn即为振荡环节的转折频率。

在阻尼比ζ较小时，G（jω）将随ω变化而出现峰值，由

可求得谐振频率ωr和谐振峰值Mr

谐振峰值与阻尼比ζ有关，因此用渐近线来表示时的误差大小与ζ值有关。表5-1是不同频率点下的幅值修正量。

图5-21 振荡环节的Bode图（所标数字为对应的ζ值）

表5-1 振荡环节幅值比修正量

表5-2是不同ζ值时的φ（ω）值，在ω＝0、ω＝和ω＝∞时相位分别为0°、－90°和－180°，与ζ值的大小无关。在Bode图中相频曲线点斜对称。

表5-2 振荡环节的相频特性φ（ω）

［例5-04］ 求解系统的谐振峰值和谐振频率。

［解］ 对应有程序

MATLAB中运行结果为

7）二阶微分环节

二阶微分环节的频率特性式分别有

G（jω）＝τ2（jω）2＋2τζ（jω）＋1

可知：

（1）ω＝0时，G（jω）＝1∠0°；

（2）ω＝时，G（jω）＝j2ζ；

（3）ω＝∞时，G（jω）＝∞∠180°。

图5-22所示为二阶微分环节的Nyuist图，从1∠0°开始由第一象限变化到第二象限，并向实轴的负端无限延伸。

二阶微分环节和振荡环节的对数幅频特性和对数相频特性不同之处也仅相差一个符号。因此绘制二阶微分环节的Bode图时，可以利用表5-1的修正值，但注意相差一个符号。

图5-22 二阶微分环节的Nyuist图

图5-23 延滞环节的Nyuist图

8）延滞环节

延滞环节的频率特性式分别有

G（jω）＝e－jωτ

∣G（jω）∣＝1　L（ω）＝20lg∣G（jω）∣＝0

∠G（jω）＝φ（ω）＝－ωτ

幅值总为1，相角与ω成线性变化。因此延滞环节的Nyquist是一单位圆（见图5-23）。Bode图中幅频为零分贝线，相频则与频率ω成线性变化。