频域修形校正网络

1）超前校正网络

如图6-8（a）所示是无源相位超前网络，有

图6-8 相位超前网络

（a）无源校正网络； （b）机械校正装置

图6-8（b）是图6-8（a）的机械相似系统，同样有

式中：T＝B1K1；α＝K1＋K2K2＞1。

式（6-1a）或式（6-1b）是超前校正网络的传递函数，当∣α∣≥1时，有

故相位超前网络近似实现了PD控制律。PD控制因为高频放大的原因不单独使用。超前校正网络相比于PD控制，分母中增加了一个一阶极点，在实现相位超前的同时抑制高频的放大效应。

“超前”是指在稳定的正弦信号作用下，可以使其输出的正弦信号相位超前的意思。图6-9为超前校正网络的Bode图，其转折频率分别为1／T和α／T。

图6-9 超前校正网络Bode图

图6-10 超前网络αφm曲线

相位超前网络提供的超前相角为

ωm位于两转折频率1／T、α／T的几何中点。如图6-10所示φm仅与α有关，α越大相位超前角φm也越大。

超前校正具有高通滤波特性，使用时需考虑对抑制噪声干扰的不利，因而α值一般不能取得太大。由图6-10的αφm曲线可看出：α取得过小时超前校正效果不显著；α取得过大时超前校正的相位超前效果变得趋缓。通常取5≤α≤15，如果需要较大的相位超前，可以采用双重超前校正，即Gc（s）＝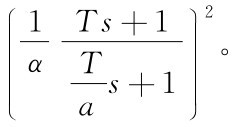

超前校正网络在低频段对数幅频特性曲线的幅值变化为

在最大相位角φm处（对应频率为ωm），幅频特性曲线的幅值变化为

式（6-1）中的系数1／α是一衰减量，α越大衰减量越严重，因此在回路中需要提高增益或附加放大环节，以避免因低频增益降低而影响精度。

2）滞后校正网络

用无源阻容元件组成的滞后校正网络如图6-11（a）所示，传递函数为

式中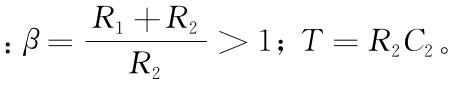

图6-11 相位滞后网络

（a）无源校正网络； （b）机械校正装置

从图6-12可看出，滞后校正网络实质是低通滤波器。高频对数幅频特性比低频幅频特性衰减20lgβd B。利用这一特性可以对开环的中高频部分加以衰减，使增益交界频率ωc减小，以提高系统的稳定裕度。或者通过增大开环增益，抬高开环的低频部分，以提高系统的稳态精度。

由图6-13的βφm曲线可看出：β越大相位滞后越严重，所以应尽量使产生最大滞后相角的频率ωm远离校正后系统的幅值穿越频率ωc，否则会对系统动态性能产生不利影响。常取

图6-12 滞后校正网络Bode图

图6-13 滞后网络βφm曲线

3）滞后超前校正网络

图6-14（a）是近似的滞后超前网络的无源阻容实现，传递函数为

图6-14（b）是图6-14（a）的机械相似系统，有同样的传递函数式，式中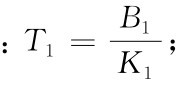

若T2＞T1、α1，则式（6-3）变为

图6-14 相位滞后超前网络

（a）无源校正网络； （b）机械校正装置

是PID控制律的近似实现。

当近似有，则式（6-3）的传递函数可近似写成

式（6-4）表明，滞后 超前校正网络实际是把滞后校正网络和超前校正网络的特性结合起来，其Bode图如图6-15所示。频率前半段是相位滞后部分，具有使后续增益衰减的作用，可用于在低频段提高增益以改善系统的稳态性能。频率后半段是相位超前部分，可用于提高系统相位裕量，增大增益交界频率ωc改善系统动态性能。由图6-15可见，随着频率增加，由相位滞后变为相位超前。当频率

图6-15 滞后超前网络的Bode图

时相位为零。