【摘要】：MATLAB中采用矢量表达多项式，即将多项式系数按降幂的次序赋给多项式矢量，同时提供多项式函数及留数计算方法。即将多项式进行因式分解得到。对于传递函数等所要求的多项式分式表达，MATLAB通过在相关函数中的输入项位置区分分子和分母。甚至相同的函数名通过不同的输入项数目来重载不同的功能。
在传递函数等控制系统模型中，常常用到多项式以及多项式分式，如传递函数中以s为变量的分子多项式，分母多项式。MATLAB中采用矢量表达多项式，即将多项式系数按降幂的次序赋给多项式矢量，同时提供多项式函数及留数计算方法。
（1）q＝poly（r）——计算由根矢量（r）构成的多项式，并将赋给多项式矢量（q）。
（2）r＝roots（q）——计算多项式矢量（q）表达的多项式的根，赋给根矢量（r）。即将多项式（q）进行因式分解得到（r）。
（3）z＝conv（x，y）——计算多项式矢量（x）、（y）表达的多项式的乘积，赋给多项式矢量（z）。
（4）v＝polyval（p，x）——计算多项式（p）在自变量取值为（x）时的多项式的值（狏）。
其中roots（）与poly（）互为反函数。
对于传递函数等所要求的多项式分式表达，MATLAB通过在相关函数中的输入项位置区分分子和分母。甚至相同的函数名通过不同的输入项数目来重载不同的功能。如［r，p，k］＝residue（B，A）函数计算由分子多项式（B）和分母多项式（A）构成的分式的留数矢量（r），极点矢量（p）和商（k），即
如果存在多重极点，如p（j）＝…＝p（j＋m），则对应改为
相应有反函数［B，A］＝residue（r，p，k），由分式的留数矢量（r），极点矢量（p）和商（k）构建多项式分式的分子多项式（B）和分母多项式（A）。
［例Ⅳ02］ 求取多项式分式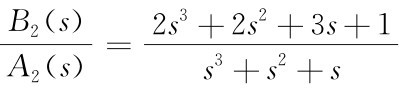
的留数。
［解］ 对应有MATLAB程序。
运行结果为
续 表
因此结果为
［解］ 对应有MATLAB程序。
运行结果为
即
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
