全概率公式和贝叶斯公式

在求解较为复杂的概率问题时，人们常常希望将所涉及的复杂事件分解成简单事件的并，而每个简单事件的概率计算相对容易，这样复杂事件的概率就得以求解.下面介绍的全概率公式，就是将样本空间适当地分解为若干部分，使得在每个部分中容易求出所要的概率.为了给出全概率公式，先给出一个定义.

对于一个样本空间来说，完备事件组不是唯一的，选择何种划分，取决于所要解决的问题.

全概率公式是概率论中最重要的公式之一，利用条件概率与全概率公式，我们可以得到另外一个重要公式——贝叶斯公式.

定理1.4.3（贝叶斯公式） 设B1，B2，…，Bn构成样本空间的一个完备事件组，A为任一随机事件，且P（A）＞0，则有

上式称为贝叶斯（Bayes）公式.

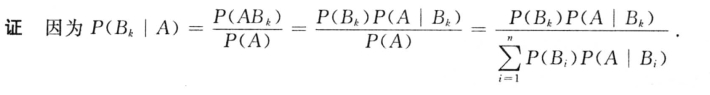
例1.4.6市场上有甲、乙、丙三家工厂生产的同一品牌产品，已知三家工厂的市场占有率分别为30% 、20%、 50%，且三家工厂的次品率分别为3%、3%、1%，（1）求市场上该品牌产品的次品率；（2）如果买了一件商品，发现是次品，问它是甲、乙、丙厂生产的概率分别为多少？

解（1）设A：买到一件次品；B1， B2， B3分别表示买到一件甲厂、乙厂、丙厂的产品；

由全概率公式，有

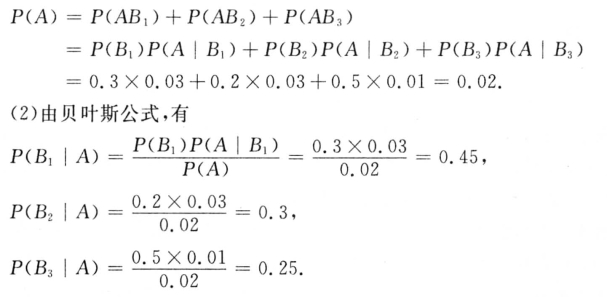
所以这件商品最有可能是甲厂生产的.

全概率公式可看成“由原因推结果”，而贝叶斯公式的作用在于“由结果推原因”，现在一个“结果”A已经发生了，我们想了解，在众多可能的“原因”中，到底是哪一个导致了这一结果？故贝叶斯公式也称为“逆概公式”.

贝叶斯公式在商业决策及其他企业管理学科中均有重要应用.

下面再举一个例子，说明贝叶斯公式在实际问题中的作用.

结果有点出乎意料，因为虽然检验法相当可靠，但被诊断为患肝癌的人真正患病的概率并不大，其主要原因是人群中患肝癌的比例相当小.当然，医生在公布某人患肝癌之前，是不会只做一次或一种检验，还会辅以其他检验手段.

正确的概率思维方式应该是现代社会中人们正确地思考问题而必备的文化修养的一个成分，它能帮助我们以更为合理的方式去观察、分析和判断事物.

思考：上题中，诊断为无病，而确实没有患病的概率为多少？

例1.4.8某物品成箱出售，每箱20只，假设各箱中含0件、1件次品的概率分别为0.8和0.2，一顾客在购买时，他可以开箱任取三件检查，当这三件都是合格品时，顾客才买下该箱物品，否则退货.试求：（1）顾客买下该箱物品的概率α； （2）现顾客买下该箱物品，问该箱确无次品的概率β.

解 设Ai：箱中有i件次品，i=0， 1；B：顾客买下该箱产品，则

（1）由全概率公式，

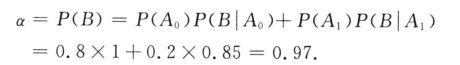
（2）由贝叶斯公式，

例1.4.9已知某城市下雨时间占一半，天气预报的正确性为0.9，某人每天上班为下雨而烦恼，于是预报下雨就带伞，即使预报无雨，他也有一半日子带伞，求：

（1）已知他没带伞，却遇到下雨的概率；

（2）已知他带伞，但天并没有下雨的概率.

解 记A：天下雨；B：预报下雨；C：他带伞.

例1.4.10设有来自三个地区的各10名、15名和25名考生的报名表，其中女生的报名表分别为3份、7份和5份.随机地取一个地区的报名表，从中先后抽出两份，

（1）求先抽到的一份是女生表的概率p；

（2）已知后抽到的一份是男生表，求先抽到的一份是女生表的概率q.