在薛定谔方程中波函数描述的是

1．薛定谔方程的建立

在前面讨论的是自由粒子的波函数，而在一般情况下，粒子总在一定的外力场中运动，为了得到描述粒子在该力场中运动状态的波函数，需要找到一个所有波函数都满足的方程，解此方程，就能得出在各种外力场作用下运动粒子的波函数ψ（r，t），这个方程就是薛定谔方程。

这个方程是1926年由奥地利物理学家薛定谔建立起来的。它是量子力学的基本方程，其在量子力学中的地位与牛顿方程在经典力学中的地位相当。薛定谔方程不是从理论上严格推导出来的，而是用类比的方法建立起来的，其正确与否只能靠实践来检验。自量子力学建立以来，将这个方程应用于分子、原子等微观系统所得到的大量结果和实验符合，这就说明了它的正确性。薛定谔因在创立量子理论方面的贡献而荣获1933年的诺贝尔物理学奖。

下面主要介绍薛定谔方程的建立过程。

设一个质量为m、动量为p的自由粒子沿x方向运动，如果不考虑相对论效应，其能量可表示为

自由粒子的波函数为

分别对波函数中的x和t求偏导，可得

将式（18－2－9）中的E和式（18－2－11）中的p2代入能量式E＝，得

这就是一维情况下自由粒子的波函数所满足的薛定谔方程。

这就是一维情况下普遍适用的薛定谔方程，它也适用于自由粒子，只不过自由粒子的势能U＝0。

如果粒子在三维势场中运动，则薛定谔方程的形式为

式中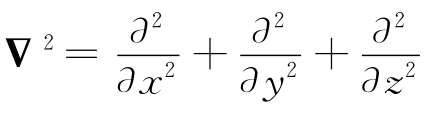，称为拉普拉斯算符。

还可以把薛定谔方程简写为

式中，，称为哈密顿算符。

2．定态薛定谔方程

在一般情况下，势能是空间和时间的函数，但在有些情况下，势能只与空间坐标有关，例如一维情况下，U＝U（x）。在这种情况下，可以把波函数分离，写成坐标的函数与时间的函数的乘积的形式，即

将其代入式（18－2－13），可得

上式中等号的左边只是时间t的函数，等号的右边只是坐标x的函数，且t和x是两个独立变量。要使等式左、右两边相等，只能是左、右两边等于同一个常量。又因为等式右边具有能量的量纲，所以这个常量是一个能量值，用E表示，即

由式（）可解得18－2－18

式中，C为积分常数。

由式（18－2－19）可解得φ（x）的具体表达形式（U（x）的表达式不同，其解φ（x）也不同）。

因此波函数可表示为

由上面的数学推导可知，能量E是一个常量，这说明在这种状态下，粒子的能量E具有确定的值。把这种能量不随时间变化的态称为定态，所对应的波函数称为定态波函数。

将式（18－2－19）变形可得

还可以简写为

式（18－2－21）就称为一维定态薛定谔方程，所解得的φ（x）称为一维定态波函数，所对应的能量E称为定态能量。

推广到三维情况，定态薛定谔方程可以写成

在关于微观粒子的各种定态问题中，把势能函数U的具体形式代入定态薛定谔方程中即可求得定态波函数，同时也就确定了概率密度的分布（｜ψ（r，t）｜2＝｜φ（r）｜2）以及能量E和角动量等。如果粒子处于束缚态，即只能在有限区域中运动时，由于波函数必须满足单值、有限、连续的条件，解出的微观粒子的能量、角动量等必定不连续，即它们是量子化的。

【例18－3】 设在宽度为a的一维无限深势阱中运动的粒子的波函数为

式中，E、a为常量，A为归一化系数。

求：（1）归一化系数A；

（2）概率密度；

（3）在何处发现粒子的概率最大。

解 （1）根据归一化条件，有

即

归一化的波函数为

（2）概率密度为

（3）当0＜x＜a时，概率密度为

令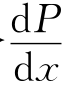＝0，可以求出极值点，即

所以

又因为0＜x＜a，故k只能取1，2，3。