等价关系与集合的分类

本节从U－SVM的角度来解释NPSVM的原理。首先对给定的训练集

我们构造一个U－SVM所需要的训练集：令负类集｛（xp＋1，－1），…，（xp＋q，－1）｝为类1，正类集｛（x1，＋1），…，（xp，＋1）｝作为Universum集，并假设存在和类1对应的另一类集合｛（xp＋q＋1，－1），…，（xp＋l，－1）｝为类2。针对此训练集，应用U－SVM对类1和类2进行分类，则得到与问题（4－2）对应的原始优化问题

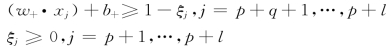
图4.1　问题（4－7）的几何解释
（Figure 4.1　Geometric interpretation of the problem（4－7）in R2）

图4.1　给出了上述问题的几何解释，一方面，其要求Universum集合（即正类点“＋”）尽可能地居于两条细红线（w＋·x）＋b＋＝－ε和（w＋·x）＋b＋＝ε所界定的ε－带内，类1（即负类点“＊”）尽可能在左侧的细红虚线（w＋·x）＋b＋＝－1左下方，而某个假设存在的类2（即点“○”）尽可能在右侧的细红虚线（w＋·x）＋b＋＝1右上方，同时其要求ε－带对应的间隔尽可能的大。下面证明一定存在着类2所对应的集，使得问题（4－7）与问题（2－45）有相同的解。

定理4.1：一定存在类2：｛（xp＋q＋1，－1），…，（xp＋l，－1）｝，使得问题（4－7）与问题（2－45）有相同的解（w＋，b＋）。

证明 设针对训练集（4－6），问题（2－45）的解为（w＋，b＋，，ξ－），显然其也是问题（4－7）的可行解。要使得（w＋，b＋，，ξ－也是问题（4－7）的最优解，则只需找到集合｛（xp＋q＋1，－1），…，（xp＋l，－1）｝，使得如下的问题最优值为0。

进一步，即找到满足

的xj，j＝p＋q＋1，…，p＋l即可。显然对已知的（w＋，b＋），一定存在着满足此不等式组的xj。

上述定理告诉我们可以通过求解问题（2－45）来代替求解问题（4－7）。换句话说，两类分类问题（负类（类1）和正类（Uninversum集合））的最优的正类点中心超平面（w＋·x）＋b＋＝0，对应着类1和类2通过U－SVM得到的最优分划超平面。而U－SVM是基于Uninversm的最大矛盾原则构建的［117］，所以NPSVM也遵循了该原则：假设F为候选函数集，基于Uninversum的最大矛盾原则构造等价类Γ1，…，Γm，该等价类将函数集划分为m个集合，每个集合中包含无穷多个等价的函数，其等价性由Uninversum集合确定。即如果某个等价类Γr中存在两个函数f（x，α1）和f（x，α2）使得

那么我们就说Universum集合中的点x＊t对等价类Γr产生一个矛盾，产生矛盾的点x＊t的个数为对该等价类大小的一个定量描述。不同的等价类对应不同的矛盾数。基于此，可以构建相应的结构风险最小化原则［120］，而U－SVM就是该原则的一个实现方法。同理，对NPSVM的第二个优化问题，仍然可以构造一个基于负类为Universum集合的U－SVM问题，使得两个问题的解相同。因此，给出了NPSVM的一种统计学习理论的解释。