引理7.1:若f(x)在x附近可微,∇f(x)≠0,则当δ>0充分小时,-Δy≠0,且-Δy为f(x)在x处的一个下降方向,其中,∇f(x)为f(x)在x处的梯度。
证明:因为∇f(x)≠0,所以-∇f(x)为f(x)在x处的一个下降方向。由f(x)在x处可微知,当δ>0充分小时,由中值定理有
即f(x+δ(-Δy))<f(x),所以-Δy为f(x)在x处的一个下降方向。
![]()
又 因为∇f(x)≠0,由引理1知,-Δy为f(x)在x处的一个下降方向,因而也是F(x, )在x处的一个下降方向。
)在x处的一个下降方向。
(注:由引理7.2知,若F(x, )<f(
)<f(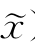 ),且‖Δy‖≠0时,-Δy为F(x,
),且‖Δy‖≠0时,-Δy为F(x, )在x处的一个降方向,可沿此方向找到更好点。)
)在x处的一个降方向,可沿此方向找到更好点。)
引理7.3:设f(x)在x处可微,∇f(x)=0,x为f(x)的一个严格极值点,若F(x, )≥f(
)≥f( )(此时F(x,
)(此时F(x, )=f(
)=f( )),且对某个Δx∈Rn,∃λ>0,当∀δ∈(0,λ):
)),且对某个Δx∈Rn,∃λ>0,当∀δ∈(0,λ):
(1)若F(x+δΔx, )≥F(x,
)≥F(x,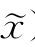 ),则在x附近,F(x,
),则在x附近,F(x,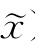 )恒为常数f(
)恒为常数f( );
);
(2)若F(x+δΔx,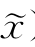 )<F(x,
)<F(x,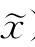 ),则x为F(x,
),则x为F(x, )的一个局部极大点。
)的一个局部极大点。
证明:(1)若x为f(x)的一个严格局部极小点,则∃x的一个邻域Nε(x),使当z∈Nε(x)时,有f(z)>f(x),而由F(x, )≥f(
)≥f( )知,f(x)≥f(
)知,f(x)≥f(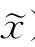 )=F(x,
)=F(x,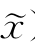 ),所以f(z)≥f(
),所以f(z)≥f( )=F(x,
)=F(x, ),所以F(z,
),所以F(z, )=f(
)=f( )=F(x,
)=F(x,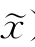 ),即在x附近,F(x,
),即在x附近,F(x, )恒为常数;若x为f(x)的一个严格局部极大点,因为F(x,
)恒为常数;若x为f(x)的一个严格局部极大点,因为F(x, )≥f(
)≥f( ),所以f(x)≥f(
),所以f(x)≥f( )=F(x,
)=F(x,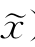 ),若f(x)=f(
),若f(x)=f( ),因x为f(x)的一个严格局部极大点,所以∃λ>0使对∀Δg∈Rn,‖Δg‖≤λ时,有f(x+Δg)<f(
),因x为f(x)的一个严格局部极大点,所以∃λ>0使对∀Δg∈Rn,‖Δg‖≤λ时,有f(x+Δg)<f( )。取δ充分小,使‖δΔx‖≤λ,则f(x+δΔx)<f(
)。取δ充分小,使‖δΔx‖≤λ,则f(x+δΔx)<f( ),所以F(x+δΔx,
),所以F(x+δΔx,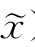 )=f(x+δΔx)<f(
)=f(x+δΔx)<f( )≤F(x,
)≤F(x, ),这与题设矛盾,故f(x)>f(
),这与题设矛盾,故f(x)>f( ),由f(x)在x处连续知,∃x的一个邻域Nε(x),使当z∈Nε(x)时,有f(z)>f(
),由f(x)在x处连续知,∃x的一个邻域Nε(x),使当z∈Nε(x)时,有f(z)>f(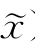 ),故F(z,
),故F(z, )=f(
)=f( )=F(x,
)=F(x,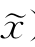 ),即,在x附近,F(x,
),即,在x附近,F(x, )恒为常数。
)恒为常数。
(2)因为F(x, )≥f(
)≥f( ),所以f(x)≥f(
),所以f(x)≥f(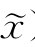 )=F(x,
)=F(x,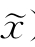 ),若x为f(x)的一个局部极小点,则∃λ>0,使对∀Δg∈Rn,‖Δg‖<λ,有f(x+Δg)≥f(x),所以F(x+Δg,
),若x为f(x)的一个局部极小点,则∃λ>0,使对∀Δg∈Rn,‖Δg‖<λ,有f(x+Δg)≥f(x),所以F(x+Δg, )=F(x,
)=F(x, ),但由题设知,∃λ>0充分小及Δx∈Rn,当∀δ∈(0,λ),有F(x+δΔx,
),但由题设知,∃λ>0充分小及Δx∈Rn,当∀δ∈(0,λ),有F(x+δΔx, )<F(x,
)<F(x, ),矛盾,故x为f(x)的一个严格局极大点;若f(x)>f(
),矛盾,故x为f(x)的一个严格局极大点;若f(x)>f( ),因为f(x)在x连续,所以∃λ>0使对∀Δg∈Rn,‖Δg‖≤λ时,有f(x+Δg)≥f(
),因为f(x)在x连续,所以∃λ>0使对∀Δg∈Rn,‖Δg‖≤λ时,有f(x+Δg)≥f( ),取δ充分小,使‖δΔx‖≤λ,则f(x+δΔx)≥f(
),取δ充分小,使‖δΔx‖≤λ,则f(x+δΔx)≥f( ),所以F(x+δΔx,
),所以F(x+δΔx, )=f(x+δΔx)≥f(
)=f(x+δΔx)≥f( )=F(x,
)=F(x, ),这与题设矛盾,故f(x)=f(
),这与题设矛盾,故f(x)=f( ),由x为f(x)的一个严格局部极大点知,∃x的一个邻域Nε(x),使当z∈Nε(x)时,有f(z)<f(x)=f(
),由x为f(x)的一个严格局部极大点知,∃x的一个邻域Nε(x),使当z∈Nε(x)时,有f(z)<f(x)=f( ),故F(z,
),故F(z, )=f(z)<f(
)=f(z)<f( )=F(x,
)=F(x, ),即x为F(x,
),即x为F(x, )的一个局部极大点。
)的一个局部极大点。
(注:由此引理7.3的情形(1)知,在‖∇f(x)‖很小的情形下,若在x附近沿某一方向无法减小F(x, ),则在x附近F(x,
),则在x附近F(x,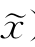 )恒为常数,可放弃在此点附近搜索;而在情形(2)中,若在x附近搜索,可进一步减小F(x,
)恒为常数,可放弃在此点附近搜索;而在情形(2)中,若在x附近搜索,可进一步减小F(x, ),从而可找到更好点。)
),从而可找到更好点。)
引理7.4:若f(x)在x处可微,∇f(x)≠0,若F(x, )≥f(
)≥f( ),则
),则
(1)当f(x)>f( )时,在x附近,F(x,
)时,在x附近,F(x,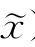 )为常数;
)为常数;
(2)当f(x)=f(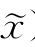 )时,-Δy是F(x,
)时,-Δy是F(x, )在x处的一个下降方向。
)在x处的一个下降方向。
证明:(1)当f(x)>f( )时,由f(x)在x处连续知,∃x的一个邻域Nε(x),使当z∈Nε(x)时,有f(z)>f(
)时,由f(x)在x处连续知,∃x的一个邻域Nε(x),使当z∈Nε(x)时,有f(z)>f( ),故F(z,
),故F(z, )=f(
)=f( )=F(x,
)=F(x, ),即在x附近,F(x,
),即在x附近,F(x, )为常数。
)为常数。
(2)若f(x)=f( ),由于∇f(x)≠0,由引理1知,-Δy为f(x)在x处的一个下降方向。所以∃λ>0,当δ∈(0,λ)时,有f(x+δd)<f(x),其中d=-Δy,所以F(x+δd,
),由于∇f(x)≠0,由引理1知,-Δy为f(x)在x处的一个下降方向。所以∃λ>0,当δ∈(0,λ)时,有f(x+δd)<f(x),其中d=-Δy,所以F(x+δd, )=f(x+δd)<f(x)=f(
)=f(x+δd)<f(x)=f(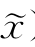 )=F(x,
)=F(x, ),因此-Δy是F(x,
),因此-Δy是F(x, )在x处的一个下降方向。
)在x处的一个下降方向。
(注:由此引理知,若∇f(x)≠0,且F(x, )≥f(
)≥f( ),则当f(x)>f(
),则当f(x)>f(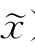 )时,沿-Δy方向搜索时步长可大一些,而当f(x)=f(
)时,沿-Δy方向搜索时步长可大一些,而当f(x)=f(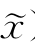 )时,步长可小一些。)。
)时,步长可小一些。)。
一维搜索是从某个点出发,沿某个方向寻找函数最优点的方法,它是加快最优化方法收敛的一种基本和有效的技术。由以上几个引理可看出,在引理7.2、引理7.3及引理7.4的情形下,若在x处沿适当方向进行一维搜索,可得出比x更好的点。据此,可设计如下基于一维搜索的杂交算子。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















