【摘要】：对这种情况，根据引理7.4，一维搜索的步长在开始时可取的较大，这样可加快一维搜索的速度，且产生的后代优于x。情形3：若‖Δy‖＜ε且F（x，）≥f（），随机产生若干搜索方向d1，…，δr∈（0，1），若对某个dj和某个δi，有F＜F（x，），则在［L，U］上对x沿dj做一维搜索，即确定α＊使令＝x＋α＊d为x的杂交后代，根据引理3，后代优于x。
设搜索空间为［L，U］⊃D，设x为一个被选择的杂交点，可按如下四种情形定义其杂交后代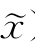
如下：
情形1：若‖Δy‖≥ε，（ε为一小正数）且F（x，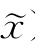
）＜f（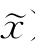
）或f（x）＝f（
），则在x处，d＝－Δy为F（x，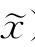
）在x处的一个下降方向，在［L，U］上对x沿d做一维搜索，即确定α＊使
令
＝x＋α＊d为x的杂交后代，根据引理7.1、引理7.2、引理7.4（2）知，后代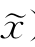
）优于x。
情形2：若‖Δy‖≥ε，且F（x，
）≥f（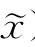
），而f（x）＞f（
），则在x处，d＝－Δy为f（x）在x处的一个下降方向，而在x附近，F（x，
）为常数，在［L，U］上对x沿d做一维搜索，即确定α＊使
令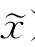
）＝x＋α＊d为x的杂交后代。对这种情况，根据引理7.4（1），一维搜索的步长在开始时可取的较大，这样可加快一维搜索的速度，且产生的后代
优于x。
情形3：若‖Δy‖＜ε且F（x，
）≥f（
），随机产生若干搜索方向d1，…，dt及若干随机数δ1，…，δr∈（0，1），若对某个dj和某个δi，有F（x＋δidj，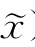
）＜F（x，
），则在［L，U］上对x沿dj做一维搜索，即确定α＊使
令
＝x＋α＊d为x的杂交后代，根据引理3（2），后代
优于x。否则，根据引理3（1），可能在x附近很难进一步减小函数值，则令后代
＝x。
情形4：若‖Δy‖＜ε，且F（x，
）＜f（
），令后代
＝x（此时x是局部极小点，且f（x）＜f（
））。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
