分类讨论，严谨思维

分类讨论，严谨思维——谈初中数学解题中的分类讨论

吴素温

数学思想是数学知识，数学技能和数学方法的本质体现，是数学的灵魂，是知识转化为能力和素质的桥梁。分类讨论是一种重要的数学思想，其实质是能够在综合性较强的问题中有意识的针对对象实施分类讨论。掌握分类的方法，领会其实质，对于加深对基础知识的理解，提高分析问题解决问题的能力是十分重要的。掌握分类的方法是首先要注意认真分析题目的条件和结论，然后根据需要再确定要分类的对象;要保证每次分类要按着同一个标准进行，并做到“不重复”，“不遗漏”。其次在分类讨论时要依据对象的限制和范围。另外还要根据题目的需要对讨论的结果进行归纳，合并，综合得出结论。下面谈谈初中数学解题中的分类讨论。

一、在使用概念时要分类讨论

在初中数学中，有些概念是分类定义的。如:绝对值的概念是从正数，0，负数三种情况定义的;两个圆相切，是由内切和外切定义的;直线和圆的位置关系等等。

例1:已知│a－1│+│a+b│=1，并且a.b均为整数，求a－b的值。

分析:│a－1│与│a+b│都是非负数，且a.b都是整数，所以只有他们其中一个是0，另一个是1。可分两类情况求出a－b的值。

解:∵│a－1│与│a+b│都是非负数，且a.b都是整数

当│a－1│=0，│a+b│=1时

∴a=1，b=0或b=－2

∴a－b=1或a－b=3

当│a－1│=1，│a+b│=0时

∴a=2时，b=－2; a=0时b=0

∴a－b=4或a－b=0

说明:本题是采用逐级分类讨论的方法，先利用非负数与正数的特性分成两类，再求出a与b的所有可能值，从而得到a－b的值。

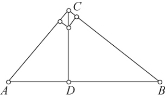
例2:如图1在Rt△ABC中，∠C=90°，AC=3，BC=4.若以C为圆心，R为半径所作的圆与斜边AB只有一个公共点，则R的取值范围是________。

分析:“以C为圆心，R为半径所作的圆与斜边AB只有一个公共点，除⊙C与AB相切外，还有圆C与线段AB”相交时也存在只有一个公共点的情况。

解:∵R为半径所作的圆与斜边AB只有一个公共点

则可分两种情况讨论:⊙C与AB相切或⊙C与AB相交，其中一个交点在线段AB上，另一个交点在直线AB上。

当⊙C与AB相切时:过C作CD⊥AB于D，CD为⊙C的半径

在Rt△ABC中∠C=90°由勾股定理，得: AC2+BC2=AB2

∴AB=5可计算: CD=2.4

∴R=2.4

当⊙C与AB相交时: R＞AC且R≦AB

∴3＜R≦4

综上所述: R=2.4或3＜R≦4。

二、在使用定理和性质时要分类讨论

在初中数学中，有些法则，性质是分类给出的，有些定理是有限制条件的，所以在应用它们的时候就要加以注意。比如不等式的性质，不等号的两边同时乘以一个数时，就要分正数，负数两种情况分类讨论，因为它关系着不等号方向的变与不变。

例3:解关于x的不等式x－2＞a－bx

分析:在不等式中有两个参变量a和b，所以在使用不等式的性质时，就要加以讨论，并确定不等式的解集。

解:∵x－2＞a－bx

∴(1+b)x＞2+a.

(1)当1+b＞0即b＞－1时，x＞(2+a)/(1+b)

(2)当1+b＜0即b＜－1时，x＜(2+a)/(1+b)

(3)当1+b=0即b=－1时，原不等式可变为(1－1)x＞2+a

∴a＜－2时，解为一切实数; a≧－2时无解

说明:不等式的解集是依据b的三种解集范围而分别给出的。在解题时，要注意b=－1时解集情况的确定。

三、在解方程或确定函数解析式时要注意分类讨论

在初中数学中，有些方程，方程组，函数解析式的系数是以字母形式给出的，在解题时要根据条件或结论进行分类讨论。这些字母取值范围的确定关系到方程的类型与解，关系到如何确定函数解析式以及求出自变量的取值范围。在讨论中要依据定义，定理去分类，还要注意挖掘隐含条件，正确分析解决问题。

如:已知关于x的方程mx2－(3m－1)x+2m－2=0

(1)求证:无论m取任何实数时，方程恒有实数根.

分析:“关于x的方程mx2－(3m－1)x+2m－2=0”这种表述没有确定方程是一元一次方程还是一元二次方程，即方程的类型是一个不确定的因素，应该分类进行讨论。

解:当m=0时，方程mx2－(3m－1)x+2m－2=0变为－x－2=0，是一个一元一次方程，显然有实数根。

当m≠0时，方程mx2－(3m－1)x+2m－2=0是一个一元二次方程，其根的判别式为［－(3m－1)］2－4m(2m－2)=(m+1)2≥0，显然也有实数根。

综合以上两种情况，故无论m取任何实数时，方程恒有实数根.

例4:已知:抛物线y=x2－(a+2)+9的顶点在坐标轴上

求: a的值。

分析:由抛物线y=x2－(a+2)+9知抛物线的开口向上，又顶点在坐标轴上，因此要分两种情况，第一，顶点在x轴上;第二，顶点在y轴上。顶点确定后，a的值就可求了。

解: y=x2－(a+2)x+9=［x－(a+2)/2］2+9－(a+2)2/4，

∴此抛物线的顶点坐标为((a+2)/2，9－(a+2)2/4).

∵抛物线的顶点在坐标轴上，

∴当顶点在x轴上时，9－(a+2)2/4=0

解得a1=4，a2=－8;

当顶点在y轴上时，(a+2)/2=0，

解得a=－2

∴a的值为4，－8，－2.

四、在确定图形的位置时进行分类讨论

在有些问题中，图形的位置是不确定的，这时就要进行分类讨论，这一类问题往往涉及到几何知识，函数知识等，带有一定的综合性。讨论的对象一般比较隐藏，解起来存在一定困难。处理这一类题目要抓住实质。首先要根据题目需要，确定讨论对象，做出分类;然后针对这些对象实施分类讨论，对于比较复杂的问题，还要进行逐级分类;最后，还要对讨论的结果进行归纳，合并，综合得出结论。做到每次分类要按照同一个标准，“不重复”，“不遗漏”，保证分类讨论的科学性与合理性。

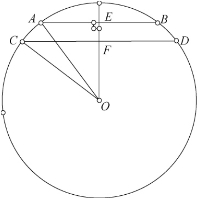
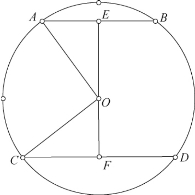
例5:已知⊙O的半径为5，两条平行弦的长分别为8和6，求两条平行弦间的距离。

分析:解此题的关键时做出弦心距，但必须考虑到两弦在⊙O中的位置有两种情况:如图3和4，利用垂径定理和勾股定理，可求的两条平行弦间的距离为1和7。

例6:已知:等腰△ABC的外接圆的半径为7，外接圆圆心到底边BC的距离为3，求AB的长。

解:此题应分两种情况，

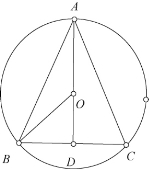
(1)顶角∠A为锐角，圆心O在△ABC内，如图4，连接AO并延长交BC于D，连结OB，

∵AB=AC，∴弧AB=弧AC

∴点A是弧BAC的中点

∴AD⊥BC，且BD=CD

∴AB=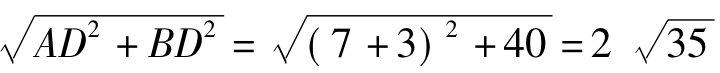

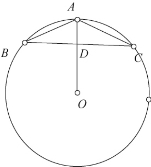
(2)顶角∠A为钝角，圆心O在△ABC外，如图5，连接AO并延长交BC与D，∵AB=AC，∴弧AB=弧AC

∴点A是弧BAC的中点

∴AD⊥BC，且BD=CD

∴AB=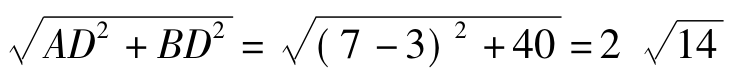

∴AB的长为　2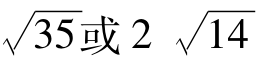　

例7:已知矩形的长大于宽的2倍，周长为12，从它的一个顶点作一条射线，将矩形分成一个三角形和一个梯形，且这条射线与矩形一边所成的角的正切值等于二分之一。设梯形的面积为S，梯形中较短的底的长为x，试写出梯形面积S关于X的函数关系式，并指出自变量X的取值范围。

分析:由于矩形的长大于宽的2倍，从它的一个顶点作一条射线，这条射线与矩形的一边所成角，可以是这条射线与长边所成角，也可以是这条射线与短边所成角。又由于矩形的长大于宽的2倍，则这条射线只与长边相交，这样就得到以下两个图:图6和图7，其他问题就可以在此基础上解决。

解:∵矩形的长大于宽的2倍，

∴AE与BC相交的情况如图所示，分两种情况。

∵AD+AB=6，AD＞2AB＞0，∴0＜3AB＜6，

∴0＜AB＜2，4＜AD＜6.

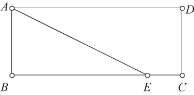
图6

图7

当AE与AD所成角tan∠DAE=1/2时(如图6)

∵AD∥BC，

∴∠BEA=∠DAE.

∴tan∠BEA=1/2，

设CE=x，AB=CD=n，可求得BE=2n，AD=2n+x，n=(6－x)/3.

由0＜AB＜2，得0＜(6－x)/3＜2.

∴0＜x＜6.

∴S梯形ADCE=－2x2/9+2x/3+4，其中0＜x＜6.

当AE与AB所成角tan∠BAE=1/2时(如图7)

设CE=x，BE=m.可求得AB=CD=2m，AD=m+x，m=(6－x)/3

由0＜AB＜2.得0＜(6－x)/3＜1.

∴3＜x＜6.

∴S梯形ADCE=－5x2/9+8x/3+4，其中3＜x＜6.

例8:在直角坐标系XOY中，一次函数 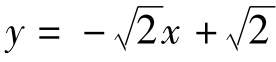的图象与x轴交于点C，与y轴交于点B，点A坐标为(－3，0)，若x轴上还有一点D，且使∠BCD=∠ABD，求图像经过B，D两点的一次函数解析式。

分析:由于以C为顶点，CB为一边，另一边在x轴的角有两个，一个是钝角，另一个是锐角。再利用有关的三角形知识，求出点D坐标，就可求出图象经过B，D两点的解析式。

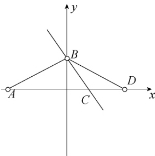
图8

图9

解:∵一次函数的图像与x轴交于C，与y轴交于B.

∴AC=4.当∠BCD与∠ABD是相等的钝角时，则点D在点C的右侧∵∠BCD=∠ABD，∠BDC=∠ADB.

∴△BCD∽△ABD

∴CD/BD=BD/AD

∴BD2=CD(AC+CD).

∵BD2=BO2+OD2，

∴2+(1+CD)2=CD(4+CD)

∴CD=3/2

∴点D(5/2，0).

∴所求一次函数的解析式为y=－2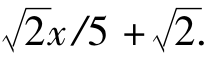

当∠BCD与∠ABD是相等的锐角时，则点D在点C的左侧，

∵∠BCD=∠ABD，∠BAC=∠BAD，

∴△ACB∽△ABD

∴AB/AD=AC/AB

∴AB2=AD* AC

∴AD=AB2/AC

∵BA2=AO2+OB2，

∴AD=(9+2)/4=11/4，

∵DO=AO－AD=3－11/4=1/4，

∴点D(－1/4，0)

∴所求一次函数的解析式为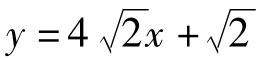

∴过B，D两点的解析式为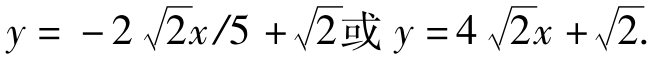

说明:要正确理解两轴上的点的坐标与两轴上两点间的距离之间的关系，并要掌握它们，正确求出点的坐标。

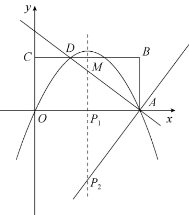
例9:矩形OABC在平面直角坐标系中的位置如图所示，A、C两点的坐标分别为A(6，0)、C (0，3)，直线与BC边相交于点D.

(1)若抛物线经过A、D两点，试确定此抛物线的解析式;

(2)设(1)中的抛物线的对称轴与直线CD交于点M，点P为对称轴上一动点，以P、A、M为顶点的三角形与△ABD相似，求符合条件的所有点P的坐标。

解:(1)∵四边形OABC为矩形，C(0，3)

∴BC∥OA，点D的纵坐标为3.

∵直线与BC边相交于点D，

∴点D的坐标为(2，3)

∵若抛物线经过A(6，0)、D(2，3)两点，

∴

解得:∴抛物线的解析式为.

(2)∵抛物线的对称轴为x=3，

设对称轴x=3与x轴交于点P1，∴BA∥MP1，

∴∠BAD=∠AMP1.

①∵∠AP1M=∠ABD=90°，∴△ABD∽△AMP1.

∴P1(3，0).………6分

②当∠MAP2=∠ABD=90°时，△ABD∽△MAP2.

∴∠AP2M=∠ADB

∵AP1=AB，∠AP1 P2=∠ABD=90°

∴△AP1 P2≌△ABD

∴P1 P2=BD=4………7分

∵点P2在第四象限，∴P2(3，－4).…8分

∴符合条件的点P有两个，P1(3，0)、P2 (3，－4).

从上述解题过程中可以看到，认真审题，挖掘隐含条件，考虑各种可能性，是解题的必要条件，要在学习中逐渐培养思维的严谨性，树立分类讨论的意识，掌握分类的方法，提高解题能力。

参考书目

［1］陈俊辉《初中数学活动课程实验与研究》海南出版社

［2］刁卫东《如何运用分类讨论思想解题》

此文获宣武区优秀论文三等奖