《直线与圆的位置关系》教学设计

《直线与圆的位置关系》教学设计

邱鹏飞

【三维目标】

1.知识与技能

（1）了解用方程法判断直线与圆的位置关系。

（2）能用几何方法判断直线与圆的位置关系。

（3）能用直线与圆的位置关系解决一些简单问题。

2.过程与方法

通过用两种方法判断直线与圆位置关系的比较，体会两种方法各自的优点与不足。

3.情感态度价值观

通过数与形的结合，体会数学的简洁美。

【教学重点与教学难点】

1.重点：线圆位置关系。

2.难点：直线与特殊圆弧的位置关系。

【教学课时】　1课时

【教学过程】

一、新课引入

1.如何求圆的方程？

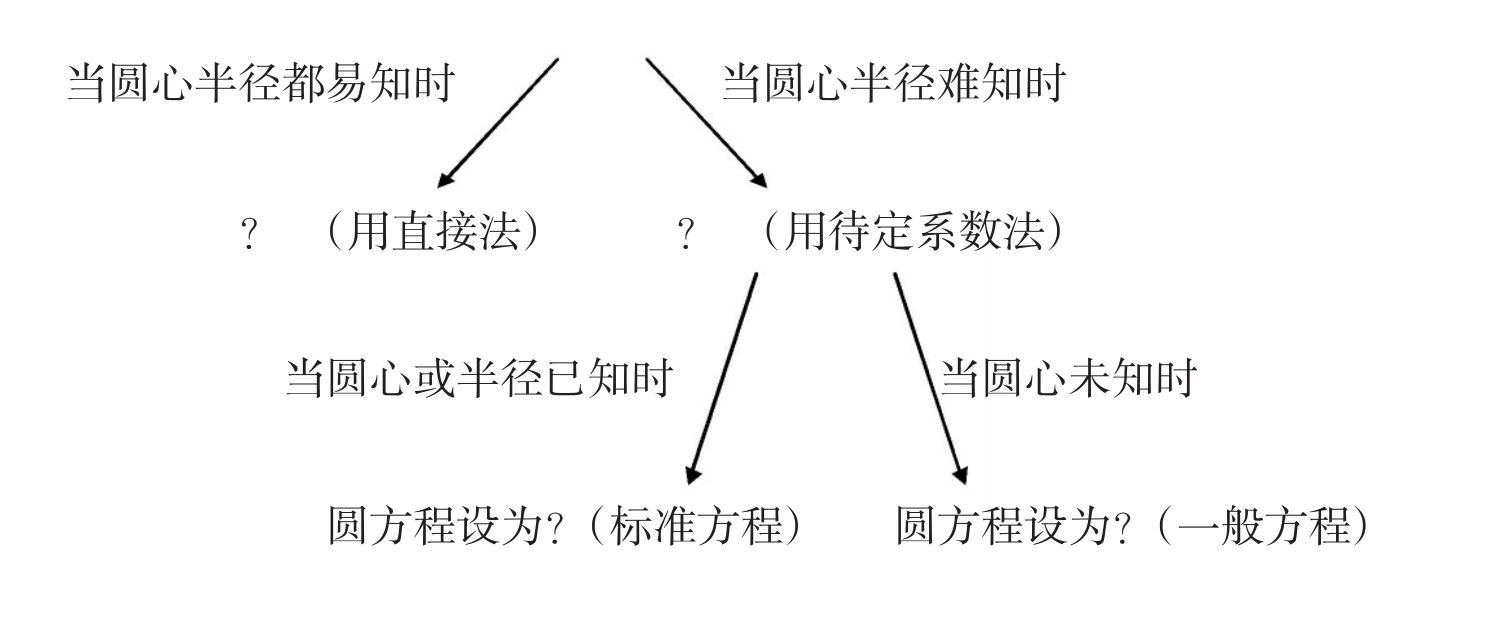
2.如何判断点与圆的位置关系？

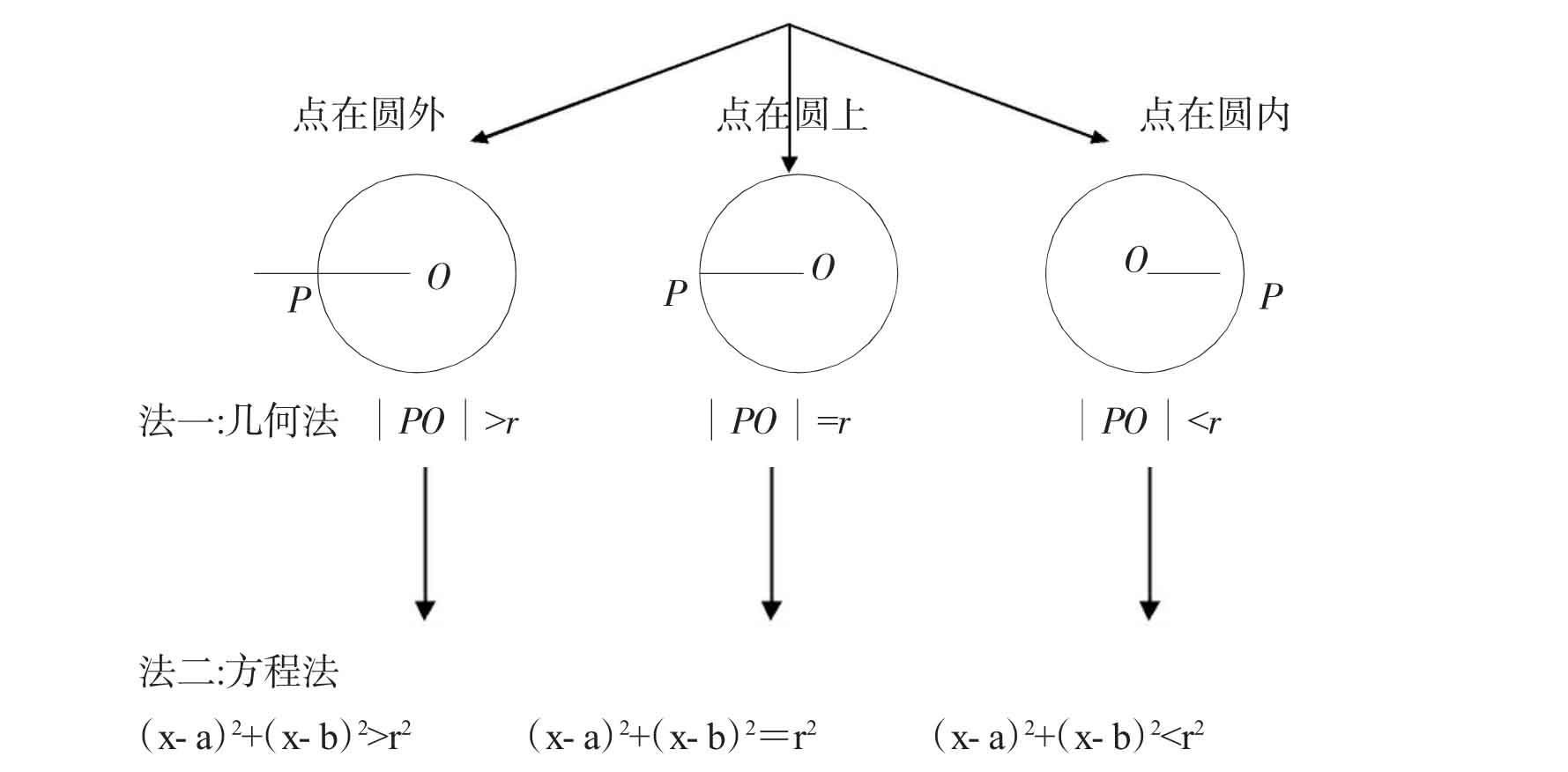
3.几何法、方程法都能判断点与圆的位置关系，那么直线与圆的位置关系是否也能用这两种方法判断呢?

二、新知探究

1.直线与圆的位置关系的判断

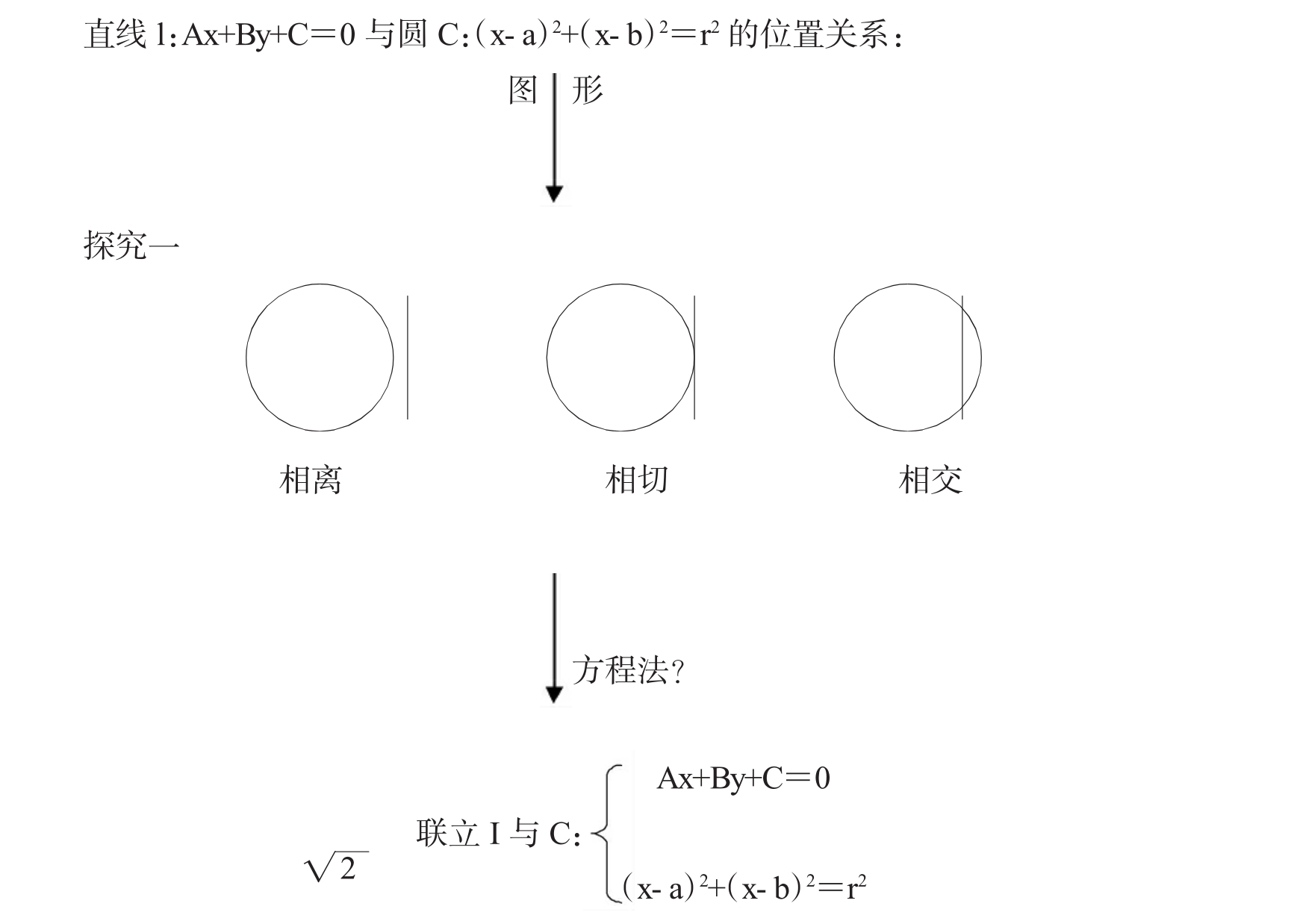
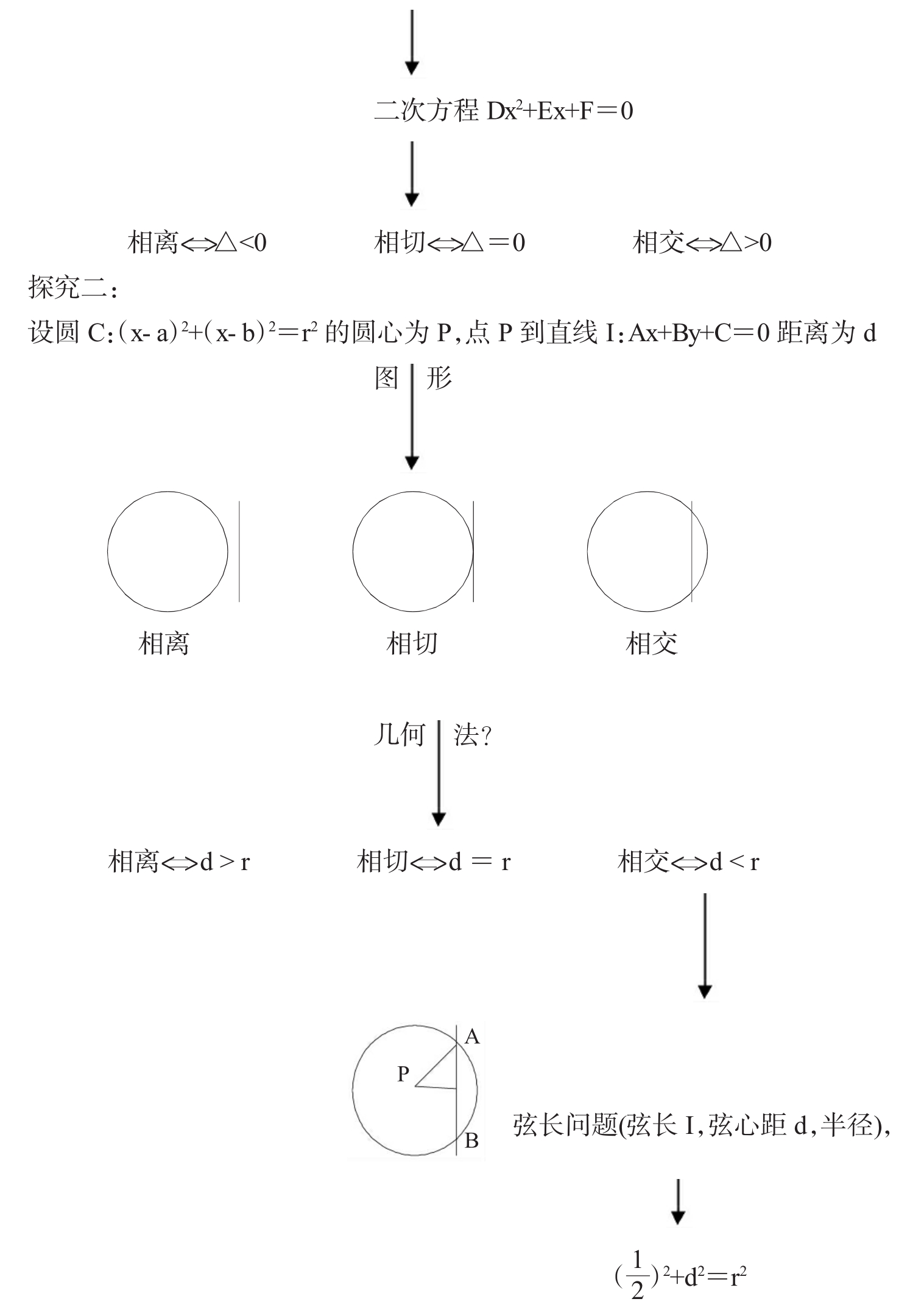
2.应用举例

例1：已知直线x+y=1与圆x²+y²-2ay=0，（a＞0）没有公共点，求a的取值范围。

引导学生共同分析：线圆没有公共点即相离

方法一：几何法　　　　　方法二：方程法

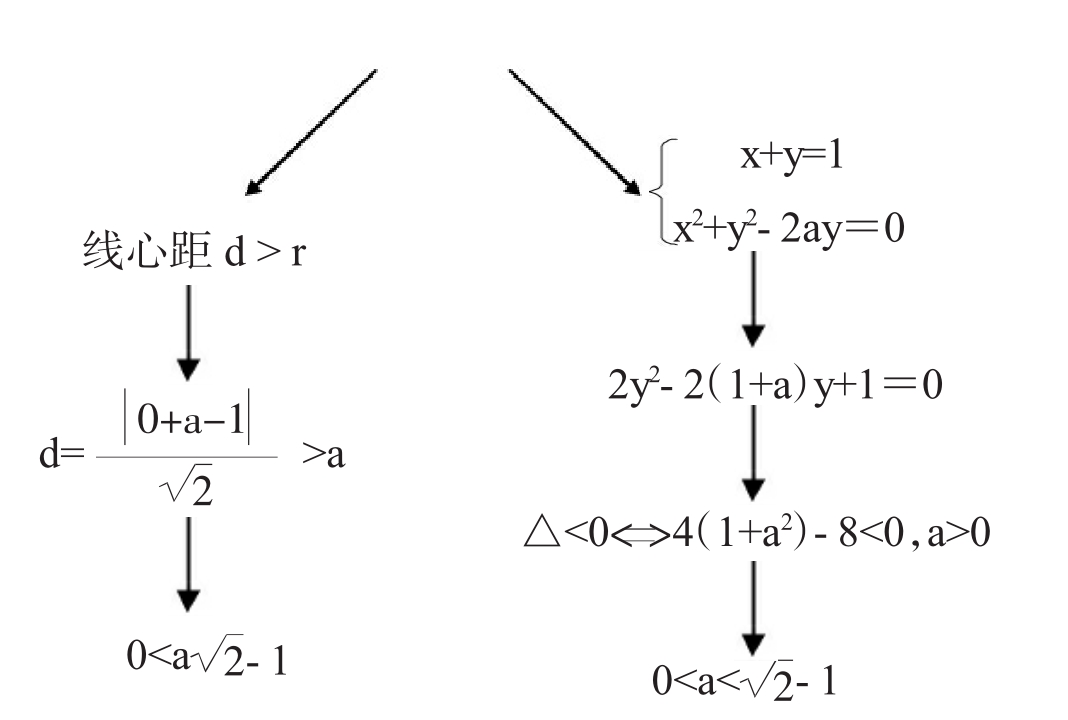
引导学生比较两种方法的优劣。在线圆位置关系问题中，哪种方法更简单？（几何法）

分析：曲线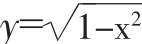是什么样的图形？（单位圆的上半部分）能否用方程法解决此题？为什么？（不能，线与半圆有一个交点＜＞线圆相切）如何用几何法解决此题？（先画图）

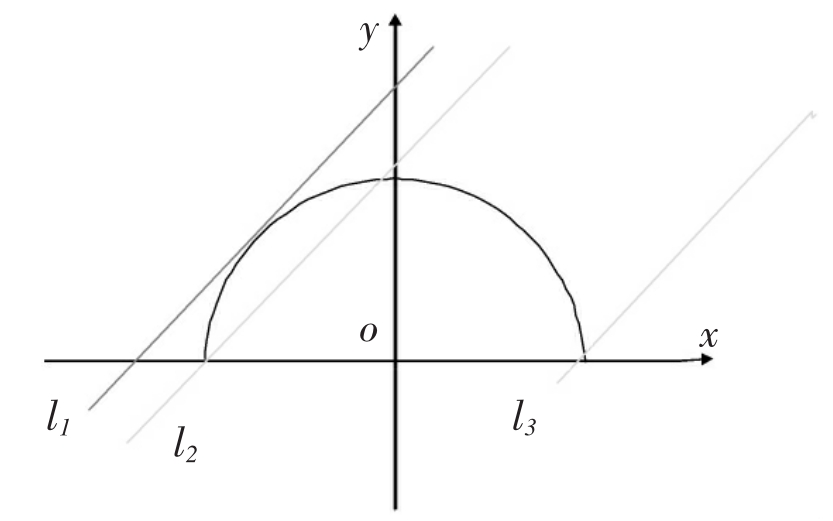
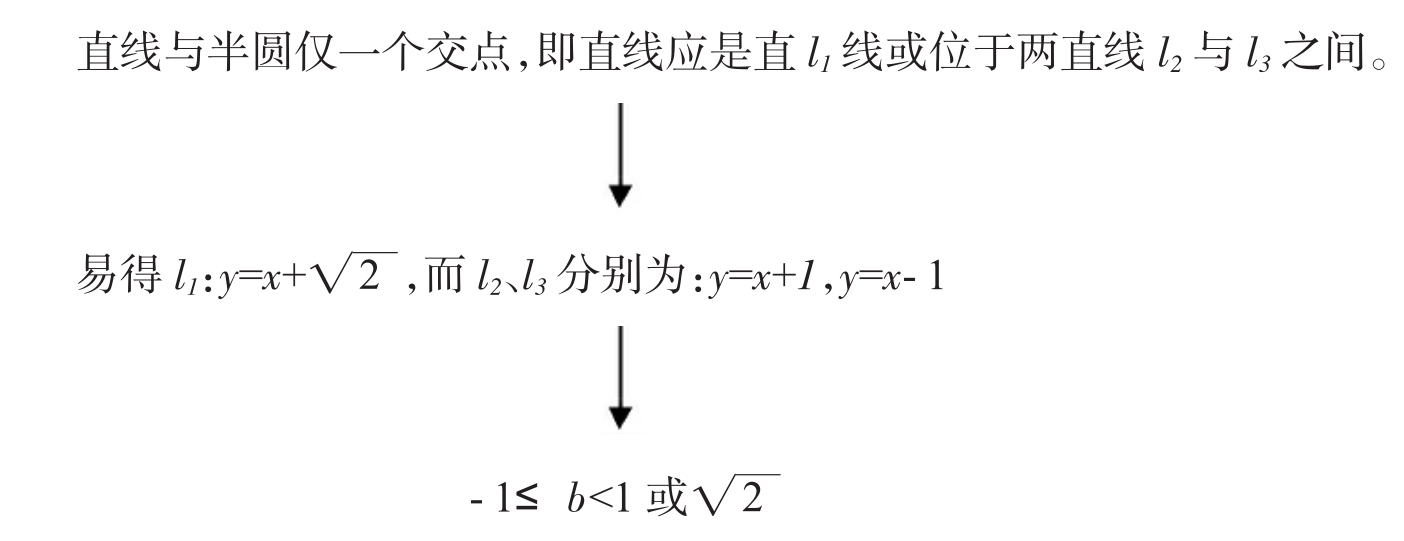
3.巩固练习

（1）（2005年辽宁）若直线2x-y+c=0按向量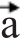=（1，-1）平移后与圆x²+y²=5相切，则c的值为（　）。

A.8或-2　　B.6或-4　　C.4或-6　　D.2或-8

先让学生思考，适时引导。

点拨：

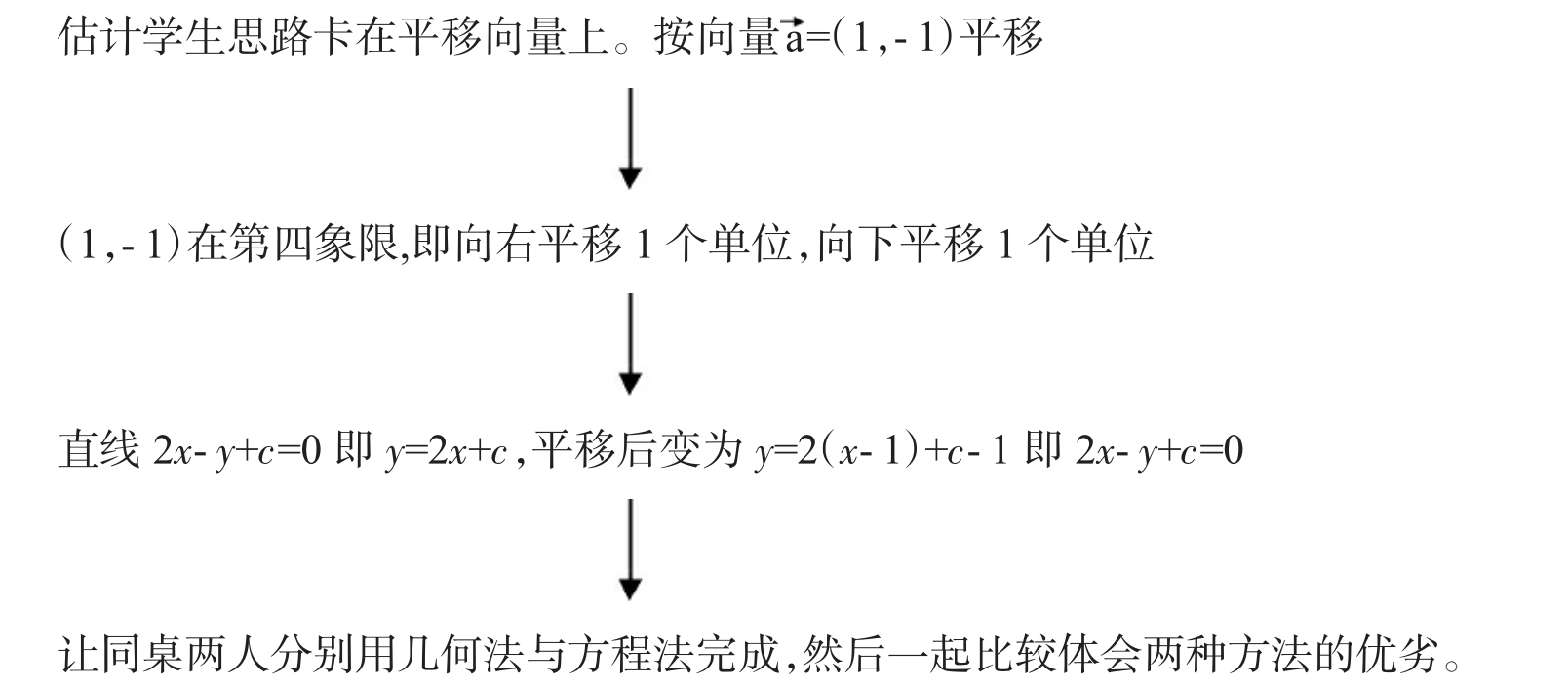
（2）（2006年天津）若直线ax-y+3=0与圆（x-1）²+（y-2）²=4相交于A、B两点，且弦AB的长为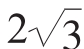，则a=____________。

此题较易，让学生先画出图形，一般学生可完成。

（3）（2007年上海）若曲线与直线x=m有且只有一个交点，则实数m=___________

【引　申】

几何法在线圆位置关系中有巨大的优越性，但几何法在线与其他圆锥曲线位置关系中是否也能大展身手呢？

【课后探究练习】

1.已知直线y=（a+1）x-1与曲线y²=ax恰有一个公共点，求实数a的值。

2.直线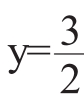 x+b与抛物线段y=x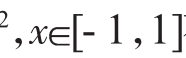有公共点，求实数b的取值范围。

【作业布置】

【课堂小结】

【板书设计】