吉克的农田

第九章　数字逻辑思维游戏

数字游戏是一种通过寻找和利用数字之间的变化规律来获得答案的智力游戏，对逻辑思维的培养具有积极的作用，被人们誉为“数字体操”，在世界上非常普及。面对数字逻辑思维游戏，很多人常常会倍感艰难，以至于望而生畏。事实上，只要掌握正确的方法，这些看似纷繁复杂的数字游戏便可迎刃而解。

分吃香蕉

张三、李四两个人出一样多的钱买香蕉，每根2角钱，两个人一共买了12根，当李四吃到第5根香蕉的时候，张三已经将第7根香蕉吃完了。于是张三对李四说:“和我相比，你多吃了两根香蕉，你应该还给我4角钱。”

请问，李四的要求公平吗？为什么？

【妙趣解析】

不公平。其实，按理说每个人各吃6根香蕉，换句话说就是，张三只不过是多吃了一根香蕉，因此只需要给李四2角钱就行了。

看脚识动物

小平和妈妈到动物园玩，回到家之后，爸爸问小平在动物园见到了多少动物，小平说自己见到了鸵鸟与斑马，但是只见到了35个头与94条腿。

请问，小平究竟见到了几只鸵鸟与几匹斑马？

【妙趣解析】

小平见到了23只鸵鸟与12匹斑马。

四个数字

有4个数字，把它们加起来，其和为50，倘若将第一个数加上4，第二个数减去4，第三个数乘以4，第四个数除以4，那么这四个数的答数就完全一样了。

请问，它们是哪4个数？

【妙趣解析】

4、12、2、32。

字母代表的数字

在下面的数学算式中，相同的字母代表相同的数字:

　　ABCDE×4＝EDCBA

请问，几个字母分别代表什么数？

【妙趣解析】

21978×4＝87912

111111111的平方

下面有3个算式:

112＝121

1112＝12321

11112＝1234321

请你推算出:111111111的平方是多少？

【妙趣解析】

12345678987654321

滚动的机器

在两根周长为0.5米的圆木上，放有一台机器，机器可以往前滚动，当圆木滚动一圈的时候，机器可以前进多少米？

【妙趣解析】

当圆木往前滚动一圈之后，它们可以让重物相对于它们往前移动0.5米，而它们相对于地面也往前移动了0.5米，因此，总共往前移动了1米。

计程表上的数字

一辆汽车匀速在公路上行驶，司机看了一眼计程表，发现是两位数，之后他又看了看手表，把时间记了下来。一个小时之后，司机再看一下计程表，依旧是两位数，然而有趣的是，第二次看到的两位数的数字顺序恰好和第一次看到的数字顺序相颠倒。一个小时又过去了，司机再看一下计程表，发现已经变成三位数了，其数字恰好是将一个0加在第一次看到的两位数中间。

请问，汽车的速度是千米/时？三次计程表上的数字分别是多少？

【妙趣解析】

汽车的速度为45千米/时，计程表上的数字分别为16、61、106。

限价买书

假期，小明和爸爸一起逛书店。小明看上了6本书，每本书的单价分别为:3.1，1.7，2.0，5.3，0.9和7.2。然而非常不巧，小明爸爸的身上只带了十几块钱。于是，爸爸建议，让小明从6本书中选出若干本，从而令单价相加所得的和最接近10元。

你可以帮助小明解决这个问题吗？

【妙趣解析】

10－0.10＝2.00＋0.90＋7.20。

10－0.10＝1.70＋2.00＋5.30＋0.90。

10＋0.10＝3.10＋1.70＋5.30。

学者的年龄

一个数学学者在自己的墓碑上刻上了这样一段话:“路过此地的陌生人，下面是我一生的经历，有兴趣的朋友可以试着算一下我的年龄，我的快乐童年在生命的前1/7；童年过完之后，我热衷于钻研学问，又花了1/4的生命。在此之后，我和一个女人结婚了。婚后第五年，我得了一个儿子，觉得人生如此幸福。然而可惜的是，我的儿子在这个世界上的时光只有我的一半。儿子死去之后，我又在忧伤中生活了4年，随之我的一生便结束了。”

根据上述信息，你可以将这位数学学者的年龄计算出来吗？

【妙趣解析】

84岁。我们可以先设数学家的年龄为x岁。根据碑文所述，我们很容易就可以列出如下方程:

x＝x/7＋x/4＋5＋x/2＋4

解方程即可解得，x＝84。

分享美酒

有两个容器，将其分别盛满8斤的酒，另外还有一个只能装3斤酒的空容器。今有甲、乙、丙、丁4人，在没有其他工具的情况下，怎样只用这三个没有刻度的容器使上述4人公平地分享到美酒？

【妙趣解析】

要想让上述4人公平地分享到美酒，步骤有些麻烦，开始三个容器是8/8/0；

（1）8/5/3，将3给甲，剩下为8/5/0；

（2）8/2/3将2给乙，剩下为8/0/3；

（3）8/3/0；

（4）5/3/3；

（5）5/6/0；

（6）2/6/3；

（7）2/8/1，将1给甲，剩下为2/8/0；

（8）2/5/3；

（9）0/7/3；

（10）3/7/0；

（11）3/4/3；

（12）6/4/0；

（13）6/1/3，将1给丙，剩下为6/0/3；

（14）8/0/1，将1给丁，剩下为8/0/0；

（15）5/0/3；

（16）5/3/0；

（17）2/3/3，将2给乙；3给丙、丁即可。

全能儿童

暑假，有关部门在社区做了一项统计:在100个儿童里面，有83人会骑自行车，有75人会游泳，有10人两者都不会。请问，有多少人既会骑自行车又会游泳？

【妙趣解析】

至少会骑车或会游泳的有100－10＝90（人），不会骑车只会游泳的有90 －83＝7（人）；所以，在会游泳的75个人里面减去只会游泳、不会骑车的7人，就是既会骑自行车又会游泳的人，即75－7＝68（人）。

女孩多少个

小本与他的朋友正在一个圆圈中跳舞，圆圈里面的每个人的两旁都是性别相同的人。倘若圆圈里面一共有12个男孩，那么女孩又有多少个？

【妙趣解析】

小本的朋友既可以是两个男孩，也可以是两个女孩。倘若她们是女孩，那么每个相邻的也一定是女孩，这样一来，男孩就不会出现了。既然题中已经出现了男孩，那么说明相邻的那两个人也必然是男孩。如此一来，结论就是圆圈中有12个男孩，女孩则一个也没有。

吉克的农田

农民吉克为了交清自己租赁的一块农田一年的地租，需要支付80美元现金以及若干千克的小麦。为此，他心中气闷，碰到人便不停地嘀咕。倘若小麦的价格是每千克75美分的话，那么这笔开销就是每英亩7美元了。然而现在小麦的市价已经大幅度提高了，涨至每千克1美元，因此所付的地租就变成了每英亩8美元。吉克认为要付的地租实在是太多了。

请问，这块农田到底有多大？

【妙趣解析】

设英亩数为x，所应支付的小麦千克数为y，那么根据题意，可以列出如下两个方程:

（3y/4＋80）/x＝7

（y＋80）/x＝8

将此方程组解出，即可得到公斤数为80千克，而这块农田的面积则为20英亩。

赶牛进村

农夫汤姆要把4头牛拉到对面的村子里去。4头牛从这个村子到那个村子，第一头牛需要走1个小时，第二头牛需要走2个小时，第三头牛需要走4个小时，最后一头牛需要走5个小时。现在打算一次同时将2头牛拉走，回来的时候，还要骑着一头牛，正常时间以两头牛中走得慢的那头所需要的时间为准。

请问，将4头牛从农夫所在的村子拉到对面的那个村子，至少需要花多少时间？

【妙趣解析】

12个小时。由于计算时间是以走得慢的牛所需的时间为准，因此可以让三牛和四牛同时走，只有这样做可以把时间节省下来；此外，回来的时候，一定要骑走得快的牛。根据这条原则，最好的办法则是:①将第一头牛与第二头牛拉到对村（费时2个小时）；②骑在第一头牛，回到本村（费时1个小时）；③将第三头牛与第四头牛拉到对村（费时5个小时）；④骑在第二头牛上面，回到本村（费时2个小时）；最后，将第一头牛与第三头牛拉到对村（费时2个小时）。

采蘑菇

甲、乙、丙、丁四个小朋友为了采蘑菇，一大早就走进了森林。采完蘑菇，他们打算回家去。从森林出来之前，每个人都把自己篮子里面的蘑菇数了一遍，四个人的蘑菇加起来一共有72只。可是，甲采的蘑菇只有一半可以吃，在回家的路上，甲将有毒的蘑菇全部都丢在了地上；乙的篮子底出现了一个小洞，不幸漏下两只蘑菇，结果被丙看见了，丙捡起来放进了自己的篮子中。这个时候，甲、乙、丙三个人的蘑菇数刚好一样。而丁在走出森林的路上，又采摘了一些蘑菇，结果他篮子里的蘑菇比先前多了一倍。从森林中走出来之后，甲、乙、丙、丁四个人坐了下来，每个人又各自把自己篮子里的蘑菇数了一遍。这一次，四个人的蘑菇数目居然都一样了。

请问，四个人打算往回走出森林的时候，每个人篮子里面的蘑菇分别是多少？走出森林之后，每个人又都有多少蘑菇？

【妙趣解析】

甲、乙、丙、丁四个人准备走出森林的时候:甲有32只；乙的数目＋2＝18（只）；丙的数目－2＝14（只）；丁的数目＝8（只）。从森林走出来之后，甲、乙、丙、丁各有16只，一共有64只蘑菇。

小猴分桃

早上，小猴按早、中、晚三餐将一天要吃的桃依次放在了三个盘子中。小猴反复看了看，感到晚餐太多了，早餐太少了。于是，它从第一个盘子里拿出来2个桃，放在了第二个盘子里面，又从第二个盘子里拿出来3个桃，放在了第三个盘子里面，再从第三个盘子里面拿出来5个桃，放在了第一个盘里面。这个时候，恰好三个盘子里面各有6个桃。小猴看了看，满意地笑了起来。

请问，小猴第一次分桃的时候，早、中、晚三餐各分得多少个桃？

【妙趣解析】

第一盘子里被拿走2个桃子，放进了5个桃子，事实上放进了5－2＝3个桃子，最后是6个桃子，那么原来有:6－（5－2）＝3（个）。第二盘子里被拿走3个桃子，放进了2个桃子，事实上拿走了3－2＝1个桃子，最后是6个桃子，那么原来有:6＋（3－2）＝7（个）。第三盘子里被拿走5个桃子，放进了3个桃子，事实上拿走了5－3＝2个桃子，最后是6个桃子，原来有:6＋（5－3）＝8（个）。小猴第一次分桃的时候，早、中、晚三餐各分得的桃子的个数分别3个、7个、8个。

妙用符号

用1、9、8、8这四个数，不改变它们的顺序，只在中间把四则运算符号与小数点加上去，就可以组成4个算数式子，使这4个算数式子的得数分别为1、9、8、8。

已知:（1×9）－（8÷8）＝8。

【妙趣解析】

0.1＋0.9＋8－8＝1，（1×9）＋（8－8）＝9，－1＋9－8＋8＝8

加法与减法

A.在1、2、3、4、5、6、7、8、9之间填上七个加号和一个乘号，使其和等于100。

B.在1、2、3、4、5、6、7、8、9中插入三个加减号，使其和等于100。

【妙趣解析】

A.1＋2＋3＋4＋5＋6＋7＋8×9＝100

B.123－45－67＋89＝100

有多少只羊

甲在草地上赶着一群羊向前走，乙牵着一头肥羊尾随在甲的后面。乙对甲说:“你这群羊应该有100只吧？”甲答道:“倘若再有这么一群，再加上半群，然后再加1/4群，再将你的一只肥羊凑进来，这样才有100只。”

请问，甲原来赶有多少只羊？

【妙趣解析】

本题来自于我国明代著名数学家程大位的《算法统宗》。

（100－1）÷（1＋1＋1/2＋1/4）＝36（只）

农夫买家畜

有个农夫买100头家畜，总共花了100元。已知1匹马需要10元，1头猪需要3元，1只羊需要5角。

请问，这个农夫各买了多少马、猪、羊？

【妙趣解析】

设牛的头数为x，猪的头数为y，羊的头数为z，可以推出如下两个方程式:

10x＋3y＋z/2＝100

x＋y＋z＝100

为了消去分数，将第一个方程中的各项都乘以2；为了消去z，再和第二个方程相减，这样就可以得到下列方程式了:

19x＋5y＝100

x与y可能有哪些整数值？一种解法是在方程的左边放上系数最小的项:5y＝100－19x，将两边都除以5得到:

y＝（100－19x）/5

再将100和19x除以5，把余数（倘若有的话）与除数5写成分数的形式，结果为:

y＝20－3x－4x/5

非常明显，表达式4x/5一定是整数，也就是x一定是5的倍数。5的最小倍数是它自身，因此可以得出y的值为1，把x，y的值带入任何一个原方程，可得z等于94。倘若x为任何比5更大的5的倍数，那么y就会变成负数。因此，这个题目只可能有一个解:马为5匹、猪为1头、羊为94只。

击鼠标比赛

美戴尔、尼本和汤米正在玩击鼠标比赛。美戴尔在10秒钟之内可以击10下鼠标；尼本在20秒钟之内可以击20下鼠标；汤米在5秒钟之内可以击5下鼠标。以上三人所用的时间是这样计算的；从开始的第一击，到最后的终结一击。他们是不是可以打成平手？倘若不会，谁最先将40下鼠标击完？

【妙趣解析】

他们不可能打成平手，最先击完40下鼠标的人是尼本。

他们三个人的点击速度是不同的。

美戴尔在10秒钟之内可以击10下鼠标，在点击10下的中间，一共有9次间隔，那么可以推算出每次点击的间隔时间为10/9秒；而在点击40下的中间，一共有39次间隔，那么他点完40下要花的时间为10/9×39＝43.33秒。

尼本在20秒钟之内可以击20下鼠标。在点击20下的中间，一共有19次间隔，那么可以推算出每次点击的间隔时间为20/19秒，而在点击40下的中间，一共有39次间隔，那么他点完40下要花的时间为20/19×39＝41.05秒。

汤米在5秒钟之内可以击5下鼠标。在点击5下的中间，一共有4次间隔，那么可以推算出每次点击的间隔时间为5/4秒，而在点击40下的中间，一共有39次间隔，那么他点完40下要花的时间为5/4×39＝48.75秒。

农民的鸡蛋

两个农民来到市场上卖鸡蛋，他们带的鸡蛋一共有100个，有趣的是，他们最后卖得了相同的钱数。第一个农民对第二个农民说:“如果我有和你一样多的鸡蛋，那么我能够换15桶油。”第二个农民则回应道:“如果我有了你那些鸡蛋，那么我只能换6＋2/3桶油。”

请问，这两个农民各有多少个鸡蛋？

【妙趣解析】

假设第一个农民有鸡蛋x个，那么第二个农民则有鸡蛋（100－x）个。第一个农民每个蛋卖15x/（100－x），因此他一共可以换取15/（100－x）×x ＝15/（100－x）桶油。第二个农民每个蛋卖（6＋2/3）/x，所以他一共可以换取（6＋2/3）/x×（100－x）桶油。因为两个人最后所卖得的钱数目相同，列出等式，便可求得x＝40，所以第一个农民有40个蛋，第二个农民有60个蛋。

最简便的运算

下面这道题如何算才最简便？

（1－1/4）×（1－1/9）×（1－1/16）×（1－1/25）×（1－1/36）×（1－1/49）×（1－1/64）×（1－1/81）

【妙趣解析】

此题这样算最简便:

（1－1/4）×（1－1/9）×（1－1/16）×（1－1/25）×（1－1/36）×（1－1/49）×（1－1/64）×（1－1/81）＝3/4×8/9×15/26×24/25×35/36×48/49 ×63/64×80/81

＝（1×3）/（2×2）×（2×3）/（3×3）×（3×5）/（4×4）×（4×6）/（5×5）×（5×7）/（6×6）×（6×8）/（7×7）×（7×9）/（8×8）×（8×10）/（9×9）

＝1/2×10/9＝5/9

篮中的李子

在古代数学经典《九章算术》中，有一道题目，其大意是这样的:“在一只篮子里面，有若干个李子，第一个人将全部李子的一半又一个取出来给第二个人，又将最后所余的一半又三个李子取出来给第三个人，最后，篮子里面就没有剩余的李子了。请问，篮子里面原有多少个李子？”

【妙趣解析】

篮子里子原有李子30个。

3÷1/2＝6（个）

（6/1）÷1/2＝14（个）

（14＋1）÷1/2＝30（个）

陶渊明的算术题

陶渊明是我国晋代著名的大文学家，他曾经发明过这样一道数学题:

每只公鸡价值五文钱，每只母鸡价值三文钱，每三只小鸡价值一文钱。现在有100文钱，打算买100只鸡。请问，在100只鸡中，公鸡、母鸡、小鸡各有多少只？

【妙趣解析】

我们可以先设公鸡为x只，母鸡为y只，小鸡为z只，由此可以列出一个方程组:

由于x、y、z必须是正整数，所以有三种可能:

公鸡4，母鸡18，小鸡78；

公鸡8，母鸡11，小鸡81；

公鸡12，母鸡4，小鸡84。

鸡兔同笼

在我国古代，流行着一道非常传统的数学题——“鸡兔同笼”。

（1）

鸡兔同笼不知数，

三十六头笼中露，

数清脚共五十双，

各有多少鸡和兔？

（2）

鸡兔同笼不知数，

头数相同已告诉，

知道脚共九十只，

请问多少鸡和兔？

【妙趣解析】

（1）鸡22只，兔14只。鸡二脚，兔四脚，如果36只全是鸡，那么还少了14双脚；当一只兔子被当作鸡算的时候，结果就会少一对，因此兔子应该为14只，鸡应该为36－14＝22（只）。

（2）鸡15只，兔15只。由于鸡兔数目是一样的，因此可以将鸡与兔编成组，从而让每组各有一只鸡和一只兔，这样一来，每一组各6只脚，总共有90只脚，应该有90/6＝15（组），因此，鸡和兔皆为15只。

韩信的士兵

韩信有一支军队，这支军队在千人以上、万人以下。有一次韩信在点兵的时候发现，倘若每行有3个人，那么就会有2个人多出来；倘若每行有5个人，那么就会有4个人多出来；倘若每行有7个人，那么就会有6个人多出来；倘若每行9个人，那么就会有8个人多出来；倘若每行有11个人，这个时候就不会有余数了。

请问，韩信总共有多少个兵？

【妙趣解析】

2519个士兵。

先将5、7、9的最小公倍数求出来，经计算为315。接着再取315的倍数，3，4，5……再减去1，可以被11整除的就是军队人数，即:315×8－1＝2519（人）。

2519÷3＝839，还有2个人剩下来；

2519÷5＝503，还有4个人剩下来；

2519÷7＝359，还有6个人剩下来；

2519÷9＝279，还有8个人剩下来；

2519÷11＝229，刚好被整除。

美丽的数字

找规律，填结果。

88×99＝

888×999＝

6666×9999＝

66666×99999＝

666666×999999＝

5555555×9999999＝

555555×999999＝

55555×99999＝

4444×9999＝

444×999＝

33×99＝

3×9＝

【妙趣解析】

88×99＝8712

888×999＝887112

6666×9999＝66653334

66666×99999＝6666533334

666666×999999＝666665333334

5555555×9999999＝55555544444445

555555×999999＝555554444445

55555×99999＝5555444445

4444×9999＝44435556

444×999＝443556

33×99＝3267

3×9＝27

单词游戏

请将下面这句话读一下:

Finished files are the result of years of scientific study combined with the experience of years.（这些完成了的文件是多年来科学研究与经验积累的成果。）

现在，请把这句话再读一遍，读这遍的时候，数一数其中一共出现了多少个“f”？

【妙趣解析】

这是一个非常经典的游戏。我们在这里给出的版本是彼得·加伯尔的。事实上，一共有6个f。“of”中的f常常会被人们忽略掉。

七边形谜题

杜登尼在数学上是一个天才，他曾提出一个七边形谜题，这个谜题极为难解。所谓七边形谜题，就是在七边形的七条边上填入1至14的数字（不可重复），从而让每边的三个数字之和等于26。

【妙趣解析】

26×7＝1821＋2＋3＋…＋14＝15×14÷2＝105

182－105＝77

所以角上的7个数字之和是77

77＝11×7

10＋12＝22

9＋13＝22

8＋14＝22

再加上11，一共7个，和是77

所以角上的7个数为:8～14

26－1＝25＝14＋11＝13＋12

26－2＝24＝14＋10＝13＋11

26－3＝23＝14＋9＝13＋10＝12＋11

26－4＝22＝14＋8＝13＋9＝12＋10

26－5＝21＝13＋8＝12＋9＝11＋10

26－6＝20＝12＋8＝11＋9

26－7＝19＝11＋8＝10＋9

（11）＋7＋（8）＋6＋（12）＋5＋（9）＋4＋（13）＋3＋（10）＋2＋（14）＋1＋（11）或者（10）＋7＋（9）＋5＋（12）＋6＋（8）＋4＋（14）＋1＋（11）＋2＋（13）＋3＋（10）

注意，括号中的数表示的是角上的数。

移动的部队

有一个移动的部队，这个队伍长约100米，宣传员为了向他们做宣传，从排尾走至排头，又从排头走至排尾。在这段时间内，这支队伍刚好行进了100米。如果队伍的速度与宣传员的速度都保持不变，那么宣传员在这期间究竟走了多少米？

【妙趣解析】

我们可以先设宣传员从排尾抵达排头时走了a米，设队伍和宣传员的速率比为m，这个时候队伍前进的距离是（a－100）米

可以推出:a/m＝a－100

设宣传员从排头返回排尾时又走了b米，这个时候，队伍也前进了（100－b）米

可以推出:b/m＝100－b。

又因为队伍在此期间一共前进了100米，所以宣传员往返一共走了（a＋b）米

可以推出:（a＋b）/m＝100

晚间聚会

汤姆总共有9个非常相熟的朋友，分别是凯特、大卫、露茜、艾米莉、简、西奥、玛莉、詹姆士、约翰。在接下去的9个星期六里面，汤姆想邀请他们一起吃晚饭，每次只请3个人，为了让这9个朋友在自己家吃晚饭时两个人之间只碰一次面，汤姆应该以哪种方法来安排邀请？

【妙趣解析】

要想将这个问题解决，你必须将9个朋友的可能组合的数目求出来。如果非用数学语言来表达的话，那么这个问题包含一个“九阶的斯坦纳三倍数系统”。但是我们可以用更简单的话来说，对于任意给定的朋友，至少要请4顿晚餐，才可以见到全部9个人。

第1天——凯特、大卫、露茜

第2天——艾米莉、简、西奥

第3天——玛莉、詹姆士、约翰

第4天——凯特、艾米莉、玛莉

第5天——大卫、简、詹姆士

第6天——露茜、西奥、约翰

第7天——凯特、简、约翰

第8天——露茜、简、玛莉

第9天——大卫、西奥、玛莉

速算24

速算24是一种世界上流传非常广泛的游戏。这种游戏不光4个人可以玩，2个人，甚至1个人也都可以玩。最常见的一种玩法是:每次将4张牌抽出来，通过加、减、乘、除四种运算符号，并且可以使用括号，不重不漏地将4张牌的4个点数各使用一次，组构一个表达式，令其结果全部都等于24。

之所以选择24这个数，是有着深刻道理的。在1～29这29个数字中，只有24的公约数最多，一共有8个，分别为1、2、3、4、6、8、12、24，这样就可以让4张牌的4个数形成24的可能性大一些。

通常而言，乘法是最快捷、最容易让人马上想到的，比如3×8、4×6、12 ×2等；其次则是简单的加法，比如14＋10、20＋4、21＋3等。在速算24游戏中，上述这些方法都是最简洁、最常用的。对下列数字组合进行观察，将上述方法尝试一下，希望你可以完成这组游戏。

（1）3、3、6、6

（2）6、8、7、9

（3）1、1、2、10

（4）7、8、10、10

（5）4、3、10、10

（6）7、3、1、2

【妙趣解析】

（1）（6÷3＋6）×3＝24

（2）8÷（9－7）×6＝24

（3）（10＋2）×（1＋1）＝24

（4）（10－8）×7＋10＝24

（5）3×10－10＋4＝24

（6）3×7＋2＋1＝24

数轴

为了达到便于计算的目的，古代数学应运而生，所以在引入现代数学体系之前，在日常生活中，就已经有各种各样形式的计算了。

古埃及时代，人们发现了一种十进制:10，100，1O00，10000，100000和1000000，然而它却没有“位”的概念，并且也没有0的概念。

在5000年之前，算盘终于出现了。这是一种相对原始可是十分有效的计算器。算盘可以说是一个数学玩具，直至今天，仍在使用。算盘既简单又有效，是少有的实惠发明之一，所以它在从一种文明传递到另一种文明的过程中，一直都没有发生变化。早在数字0还没有出现之前，算盘就已经学会用一个空栏来代替它的计算了。

古希腊人用字母表上的全部字母来代表数字。古罗马人的计算系统和古希腊人基本相似，只是他们是用几个特定的字母及字母组合来代表数字的。大约在公元前200年，0这个数字在历史上第一次出现了，当时它被刻在古巴比伦的一块陶板上。而有理数（包括分数）则出现得比较早，在公元前1500年的古埃及的《莱茵德纸草书》中就已经有了。之后，毕达哥拉斯学派在公元6世纪发明了一个数，它无法被归类到任何一种已知的数中。这个数的发现也就相当于证实了正方形的对角线是无法测量的。

直到今天，这个问题仍旧没有得到解决:人类所发现的第一个无理数到底是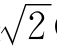 （根据毕达哥拉斯定理，等于直角边均为l的三角形的斜边），还是π（圆周率）？

负数直到1545年才全部进入数学体系，其标志是意大利数学家卡尔达诺《大衍术》的发表。

印度人在公元后的前几个世纪就发明了“位”的概念，他们用10个符号来分别表示0和前9个自然数。尽管这个系统十分先进，但是直到13世纪，它才通过阿拉伯人传到了西欧，而它的被采用又经过了几个世纪。

请问，是否所有的实数都可以在数轴上表示呢？

【妙趣解析】

数轴是这样的一条直线，它上面没有任何间隙或者空白。它包含所有的实数，即所有的有理数和无理数都可以在数轴上找到它们的位置。

拖拉机站

楚蜉是一个会计，他让4个孩子每人随便想个四位数。然后，楚蜉对孩子们说道:“把数字的第1位数挪到最后一位上，接着将这个数和原数加起来，如，1234＋2341＝3575。你们都将相加之后的结果告诉我。”

老大说:“8621。”

老二说:“4322。”

老三说:“9867。”

老四说:“13859。”

楚蜉听后，严厉地说道:“除了老三之外，你们其余几个都算错了。”

请问，楚蜉是如何知道的呢？

【妙趣解析】

任意一个四位数都可以写成:1000a＋100b＋10c＋d

把第一位转换到最后:1000b＋100c＋10d＋a

两式之和为:1001a＋1100b＋110c＋11d

非常明显，这个方程式可以被11整除，而4个孩子的答案中只有老三说的数可以被11整除。

铅弹的体积

一队建渠人需要一块某种尺寸的铅板，然而铅已经用完了。他们决定熔化一些铅弹，然后铸成铅板。可是，他们首先得对铅弹的体积进行测量。有人说给所有的铅弹称重，接着再除以铅的体重，然而没有一个人记得铅的比重是多少。有人说把铅弹倒入容量为5升的罐子中，然而是铅弹无法被压缩整合成一整块放入罐子中。有人建议测量一个铅弹的球体数据，接着就用球体积公式进行计算，最后再乘以铅弹的数目。然而这种方法实在太费时间了，并且铅弹的大小各不相同。

请问，你有什么好办法吗？

【妙趣解析】

将铅弹放入罐子中，接着往罐子中加满水，水会将各个铅弹之间的间隙占满。将铅弹拿出来，对罐子中水的体积进行计算，接着用罐子的体积减去水的体积，就可以将铅弹的体积求出来了。

拖拉机站

镇上有3家拖拉机站，第一家站借给第二家站和第三家站的拖拉机数目刚好和它们各自拥有的拖拉机数目相等。几个月之后，第二家站借给第一家站和第三家站的拖拉机数目与它们各自拥有的拖拉机数目相等。又过了一段时间，第三家站借给第一家站和第二家站的拖拉机数目与这两家站各自拥有的拖拉机数目相等。最后，3家站都有24台拖拉机。

请问，原来这些站各有多少台拖拉机？

【妙趣解析】

这个问题可以通过逆推法来解决:

可以推出:第一家站原来有39台拖拉机，第二家站原来有21台拖拉机，第三家站原来有12台拖拉机。

阿基米德定律

公元前287年，在地中海西西里岛的叙拉古，古希腊著名的数学家和物理学家阿基米德诞生了。

阿基米德的父亲也是一位天文学家和数学家，从很小的时候，阿基米德就深受父亲的影响，尤其喜欢数学。11岁的时候，阿基米德来到了尼罗河畔的亚历山大城学习，这是当时最著名的文化中心。在这段时期，为了解决利用尼罗河水灌溉的问题，他发明了有名的阿基米德螺旋（螺旋扬水器）。回到叙拉古城之后，他继续研究数学和物理学方面的难题。

在阿基米德的一生中，有很多的发现和发明，其中最著名的当数浮力定律，也就是阿基米德定律。关于这个定律，在历史上还流传着一个令人深思的故事。

亥尼洛国王命工匠做了一顶金王冠。做好之后，他又怀疑工匠将一部分金子用银子替代了，于是命令阿基米德鉴定它是不是纯金制的，前提是不能损坏王冠。阿基米德面对着这顶王冠，苦苦思索了一整天，某日，阿基米德在浴室里面洗澡，他进到浴桶中，当身子浸入浴桶的时候，一部分水就从桶边溢了出来。这个现象让阿基米德的头脑中闪过了一道闪电，“我找到了！”阿基米德大呼道，竟忘记了自己还裸露着身子，他从浴桶中一跃而出，忘乎所以地奔向街头，狂呼道:“攸勒加，攸勒加（找到了）！”就在这一欢呼声中，流体静力学正式诞生了。

要测量一个物体的密度大小，可以把它放入一个盛满水的容器中，用它排出的水量来计算。这个物体所排出的水的重量，我们称之为该物体的浮力。而该物体的重量与它所排出的重量之比，我们称之为该物体的比重。

第一步:找一块与王冠重量相等的金块；

第二步:把王冠和金块分别浸入一个盛满水的容器中，然后分别计算它们所排出的水的体积。

请问，阿基米德这个实验的结论是什么？

【妙趣解析】

倘若金块与王冠所排出的水的体积相等，那么就说明王冠是纯金的。然而当时这个实验的结果并非如此，相反，王冠排出的水的体积更大。这说明王冠并不是纯金的，因此王冠的体积才会比金块的体积大。

除了这个发现，阿基米德在其他的领域也有很大的作为。他发现了每个浸在水中的物体都受到一个水对它的向上的作用力（也就是说，物体变轻了），这称之为浮力，而物体的浮力等于该物体排出的水的重量，由此而出现了流体静力学。

在阿基米德之后，这个方法被很多人用来鉴别金属、珠宝以及测量物体的密度。另外，根据阿基米德定律，物体的质量与该物体等体积的水的质量之比，我们称之为该物体的比重。即:比重＝物体的质量/等体积的水的质量。

四个“4”

马丁·加德纳曾经把下述游戏收进了他的《数学游戏》专栏中。

游戏的规则是把数字4使用4次，通过简单的加减乘除，展开尽可能多 的数，可以使用括号。

例如:

1＝44/44

2＝4/4＋4/4

3＝

4＝

5＝

6＝

7＝

8＝

9＝

10＝

…………

【妙趣解析】

20以内，唯一不能被这样展开的数是19。倘若可以用阶乘的话，也能够将其展开（4！＝1×2×3×4），19可以被写成4！－4－（4/4）。

1＝44/44

2＝4/4＋4/4

3＝（4＋4＋4）/4

4＝4（4－4）＋4

5＝＼［（4×4）＋4＼］/4

6＝4＋＼［（4×4）/4＼］

7＝4＋4－（4/4）

8＝4＋4＋4—4

9＝4＋4＋（4/4）

10＝（44－4）/4

…………

分甜饼

小阿里阿德涅正烦着呢！今天早上，小阿里阿德涅收到了妈妈亲手做的一包新鲜小甜饼。当她把礼物打开的时候，她的4个朋友刚好来到了她的宿舍，她们提醒小阿里阿德涅，前面几次她们带的小甜饼也曾与她一起分享过，现在也该她回敬了。小阿里阿德涅很不情愿地将其中的一半以及半个甜饼分给了自己的朋友劳拉；接着又将剩下的一半甜饼以及半个甜饼分给了另一个朋友梅尔瓦；然后，她又将剩下的一半甜饼以及半个甜饼分给了朋友罗伦；最后，她又将盒子里剩下的一半甜饼以及半个甜饼分给了朋友玛戈特。这样一来，盒子里面的甜饼全部都被分了出去，可怜的小阿里阿德涅真是伤心到了极点。

请问，盒子里面原本有多少小甜饼？需要说明的是，在分甜饼的过程中，小阿里阿德涅自始至终都没有将盒子中的甜饼切成或者掰成两半。

【妙趣解析】

事实上，小阿里阿德涅总共收到了15块小甜饼。劳拉得到了7.5＋0.5，也就是8块甜饼。这个时候还剩下7块甜饼；梅尔瓦得到了3.5＋.0.5，也就是4块甜饼，这个时候还剩下3块甜饼；罗伦得到了1.5＋0.5，也就是2块甜饼，这个时候还剩下1块甜饼；玛戈特得到了0.5＋0.5，也就是1块甜饼，而小阿里阿德涅则1块甜饼也没有得到。

黑点上的硬币

在一块盾牌的周围有12个黑点，按照下面的规则，把11枚硬币放在11个黑点上。可以从任何一点开始，接连数6个点，然后将一枚硬币放在第六个点上。总是按照顺时针方向进行，从另外一个空点开始，绕圆圈计数，并把另外一枚硬币放在一个空点上。依此类推，直到将全部的硬币都放在不同的点上。计数的时候，把放有硬币的点看作是空点，并且将这个点计算在内。需要注意的是，你必须总是从一个空点开始计数。

【妙趣解析】

从任何一个点开始，数6个点，把1枚硬币放在第六个点。将你开始记数的那个点记住，也就是你放第二枚硬币的地方。从那个可以数到第一个点的点开始计数，把第三枚硬币放在可以数到第二格硬币开始的点。依此类推，把余下的硬币放在各自的点上。

硬币的面值

将一枚面值为偶数（比如，一枚2分硬币）递给你的朋友，再将一枚面值为奇数（比如，一枚5分硬币）的硬币交给他。让他每只手都握一枚硬币。让他把右手中的硬币的面值乘以3，左手中的硬币面值乘以2，接着将得到的2个数加起来。倘若得到的和是偶数，那么面值为偶数的硬币在他的右手中；倘若是奇数，那么面值为偶数的硬币在他的左手中。

请问，这究竟是什么原因？

【妙趣解析】

如果偶数面值硬币在左手，则:

　　右手（×3），即奇数×3＝奇数

　　左手（×2），即偶数×2＝偶数

　　和:奇数＋偶数＝奇数

如果偶数面值的右手，则:

　　偶数×3＝偶数

　　奇数×2＝偶数

　　和:偶数＋偶数＝偶数

倘若乘以3和2以外的其他奇数与偶数，这个小陷阱仍然成立。

正方形地毯

地毯商阿布杜近日遇到了一个大麻烦。在太阳落山之前，他必须把一个边长10米的正方形地毯交给一个非常富有的客户。他在仓库里找出一个长12米宽9米的地毯，他打算用这个地毯来做客户所要的地毯。然而，当他把这个地毯展开的时候，却发现中间已经被剪掉了一块，被剪掉的部分长8米宽1米。但是，老练的阿布杜却很快想出了一个解决问题的办法，他将剩下的地毯剪成了两块，接着再缝在一起，这样便做出一个一整块边长为10米的正方形地毯。

请问，阿布杜是如何做到的呢？

【妙趣解析】

他先沿着两条相同的虚线把地毯剪开，接着再将上半部分的地毯向左下方移动，这样，就正好可以与下半部分的地毯合并在一起了，最后再将它们缝合成一个完整的正方形地毯。

哪家公司薪水高

单从招聘启事来看，玫瑰公司和紫罗兰公司的待遇在很多方面都是一样的，只在以下两项略有不同:

玫瑰公司:a.半年工资50万元；b.工资每半年增加5万元。

紫罗兰公司:a.年工资100万元；b.工资每年增加20万元。

在这两家公司中，琼斯先生想到待遇比较优厚的公司工作，所以，他将会选择哪家公司？去该公司工作，将比他去另一家公司每年多收入多少元？

【妙趣解析】

琼斯先生应该选择玫瑰公司，去这家公司就职，将比去紫罗兰公司每年多收入5万元。事实上，只要将两个公司每年的收入都计算出来，便可以一清二楚了。

第一年:玫瑰公司:50万元＋55万元＝105万元；紫罗兰公司:100万元。

第二年:玫瑰公司:60万元＋65万元＝125万元；紫罗兰公司:120万元。

第三年:玫瑰公司:70万元＋75万元＝145万元；紫罗兰公司:140万元。

下面的都可以依此类推。由此可知，到玫瑰公司工作，每年都可以多收入5万元。

钓鱼分成

有5个男孩，我们分别以A、B、C、D、E表示。某一天，他们一起出去钓鱼，A和B一共钓到了14条鱼，B和C一共钓到了20条鱼，C和D一共钓到了18条，D和E一共钓到了12条，而A和E两人各自钓到了相同数目的鱼。

为了合理瓜分他们的战利品，5个孩子采取了下面的办法:C将他钓到的鱼与B、D两人钓到的鱼合在了一起，之后3个人各取三分之一。其余的孩子也做了一样的事，说明白点就是，每个孩子都和他的左、右两位伙伴将他们钓到的鱼合在了一起，分成数目相同的三份，然后3个人各取一份。D 与C、E联合，E与D、A联合，A与E、B联合，B与A、C联合。让人惊奇的是，经过这5次的联合后再分配，每次都可以分成数目相同的3等份，从来都没有将一条鱼再分割成分数。整个瓜分进程结束之后，5个孩子的手上都分到了相同数目的鱼。

请问，瓜分之前，每个孩子各自钓到了多少条鱼？

【妙趣解析】

从表面上来看，由于A可能钓到0～11条鱼，而其他人钓到的鱼可以据此推算出来，所以每个人钓到的鱼好像可以是33条至43条之间的任一数目。然而，由于最后每个男孩的手上分到的鱼数目相同，因此总数一定是35 或40。倘若试一下后者，我们就会发现，它能够满足全部的条件。这样一来，就可以求得A钓到了8条鱼，B钓到了6条鱼，C钓到了14条，D钓到了4条，E钓到了8条。在B、C、D三人将他们各自钓到的鱼混在一起之后，再分成数目相同的3等份，每个人可以分到8条鱼。之后，无论他们如何混在一起分鱼，每个人分到的总是8条鱼。

在市场

小艾与小贝是邻居，每天在市场上，都可以看到她们卖小鸡的身影。小贝每天卖30只小鸡，每2只卖1元，一共能够卖得15元。小艾每天也卖30只，每3只卖1元，一共能够卖得10元。有一天小艾生病了，于是请小贝帮她卖30只小鸡。这样一来，小贝去市场的时候，一共带了60只小鸡。小贝决定每5只卖2元，一共可以卖得24元。结果，和两个人分别卖的时候所得的钱相比，这样卖要少1元。

请问，这里面究竟是怎么回事？

【妙趣解析】

倘若根据正常计算，小艾和小贝分别会卖得15元和10元，总共为25元。当小贝带60只小鸡到市场上后，在每5只小鸡中，有2只是自己的，3只是小艾的，这样直到卖完小艾的小鸡；然后，小贝开始卖自己剩下的10只小鸡。根据道理来说，小艾自己的5只小鸡的价钱应为2.5元，然而在最后两笔交易中，她每次都损失了5角。因此，最后还是少了1元。