“分类讨论思想”的考情分析与研究
宋俊浩
分类讨论思想是数学思想方法中最基本、最常见的一种思想方法,分类讨论的思想方法题型覆盖知识点较多、综合性强、具有明显的逻辑性等特点,解析时需要学生有一定的分析能力、一定分类技巧,对学生能力的考查有着重要的作用。
从近三年江西和全国高考数学试题中不难发现,有关分类讨论的数学命题所占的比重还是比较大的,题型主要集中在选择题和解答题,有时填空题也会涉及到,其难度在0.4~0.6之间。覆盖的知识点比较广泛,从历年全国各地高考试题来看考点涉及到高中数学的各个方面,排列组合、概率、三角、函数、不等式、数列、圆锥曲线等等都在考查范围之内。但运用分类讨论思想最多的还是有关概率应用题,其次是函数单调性的讨论和解含有参数的不等式。具体来说,高考对分类讨论思想的考查,有以下几个方面:
一是考查有没有分类意识,遇到应该分类的情况,是否想到要分类,什么样的问题需要分类;
二是如何分类?即要会科学地分类,分类要标准统一,不重不漏;
三是分类之后如何研究;
四是如何整合?审题时一定要分清讨论的目标是自变量还是参数,当讨论自变量时结果取交集,当讨论参数时注意分情况写出;
本文试图从三个方面对历年高考试题中涉及的分类讨论思想的命题进行分析与研究。
一、基础知识、基本技能考情的分析与研究
这一类命题的基础知识点主要有集合、不等式、函数、数列、排列组合、二项式、概率等,题型以选择填空为主。能力方面主要考查学生是否具有简单分类的思想,因为这一类命题自身具有分类讨论的要求,像排列组合中的加法原理、分段函数、分段数列自变量的要求等等都是需要分类处理的。
例1(2010.全国I.理.5) 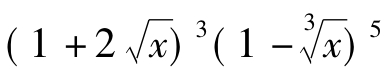 的展开式中x的系数是( )
的展开式中x的系数是( )
A.-4 B.-2 C.2 D.4
当m=0时,n=3,展开式中x的系数是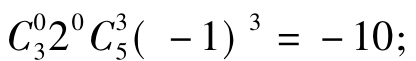
当n=0时,m=2,展开式中x的系数是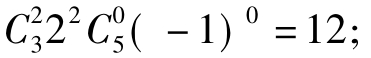
故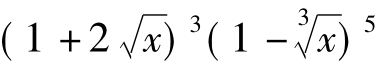 的展开式中x的系数是-10+12=2,选C。【点评】本小题考查考生是否具有简单分类意识,绝大多数的考生都能运用公式求出一个二项展开式中的系数,对于两个二项式相乘,如何求展开式中x的系数?只需将各自的通项公式相乘,令的次数为1,便有
的展开式中x的系数是-10+12=2,选C。【点评】本小题考查考生是否具有简单分类意识,绝大多数的考生都能运用公式求出一个二项展开式中的系数,对于两个二项式相乘,如何求展开式中x的系数?只需将各自的通项公式相乘,令的次数为1,便有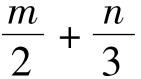 =1,对于含有两个未知数的方程,只需简单分类,各个击破。这种分类意识源于其本身的运算需要引起的,因分类标准唯一,难度不大。
=1,对于含有两个未知数的方程,只需简单分类,各个击破。这种分类意识源于其本身的运算需要引起的,因分类标准唯一,难度不大。
例2(2009.山东.理.13) 不等式|2x-1|-|x-2|<0的解集为______。
【解答过程】原不等式等价于不等式组①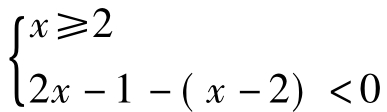 或②
或②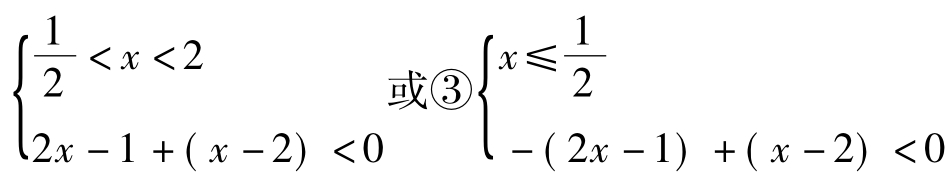 ,不等式组①无解;由②得
,不等式组①无解;由②得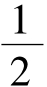 <x< 1;由③得-1<x≤
<x< 1;由③得-1<x≤ 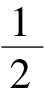 ,综上得-1<x<1,所以原不等式的解集为{x|-1<x<1}。
,综上得-1<x<1,所以原不等式的解集为{x|-1<x<1}。
【点评】去绝对值常用的方法是根据自变量的取值范围分类讨论或两边平方。但这道题采用平方去绝对值效果更好,原不等式等价于(2x-1)2<(x-2)2,求得-1<x <1,所以原不等式的解集为{x|-1<x<1}。
因此,对于分类讨论题不要急于直接进行分类讨论,首先应认真审查题目的特点,考虑是否可以用合适的公式、法则,能否进行某种变形,可否改变常规的思维方式和解题策略,若能,则可以避免进行繁杂的分类讨论。
二、灵活运用考情的分析与研究
这一类命题的基础知识点主要有函数、不等式、数列、圆锥曲线,题型以解答题为主。能力方面主要考查学生思维的严谨性,要求学生能够用辩证的眼光看待事物。处理这一类问题时往往需要“化整为零,各个击破,最后积零为整”的思维策略。
例1(2010.新课程.全国.文.21) 设函数f(x)=x(ex-1)-ax2。
(Ⅰ)若a=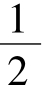 ,求f(x)的单调区间;
,求f(x)的单调区间;
(Ⅱ)若当x≥0时,f(x)≥0,求a的取值范围。
【解答过程】(Ⅰ)时a=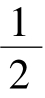 时,f(x)=x(ex-1)-
时,f(x)=x(ex-1)-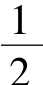 x2,f'(x)=ex-1+xex-x=(ex-1)(x+1).
x2,f'(x)=ex-1+xex-x=(ex-1)(x+1).
当x∈(-∞,-1)时,f'(x)>0;当x∈(-1,0)时,f'(x)<0;当x∈(0,+∞)时,f'(x)>0.
故f(x)在(-∞,-1),(0,+∞)单调增加,在(-1,0)单调减少。
(Ⅱ) f(x)=x(ex-1-ax).令g(x)=ex-1-ax,则g'(x)=ex-a。
若a≤1,则当x∈(0,+∞)时,g'(x)>0,g(x)为增函数,而g(0)=0,从而当x≥0时g(x)≥0,即f(x)≥0。
若a>1,则当x∈(0,ln a)时,g'(x)<0,g(x)为减函数,而g(0)=0,从而当x∈(0,ln a)时g(x)<0,即f(x)<0,综上,a的取值范围为(-∞,1]。
【点评】本小题考查函数、导数、不等式等基础知识,运用导数解决函数的单调性问题,考查了函数与方程思想、分类讨论思想。第一问是基础题,不涉及讨论,根据导函数的正负情况可求得单调区间。
第二问因为参数a的取值范围不确定,因此需要分类讨论。若g'(x)=0是超越方程,根本就无法求解时,该如何处理呢?像(2010.新课程.全国理.21题)设函数f (x)=ex-1-x-ax2.(Ⅱ)若当x≥0时f(x)≥0,求a的取值范围。
由于f'(x)=ex-1-2ax=0根本无法求出极值点,因此可以考虑用放缩法先求出满足f'(x)≥0成立的充分条件对应a的取值范围,再否定此外a取其他值不符合题意。
由(Ⅰ)知ex≥1+x,当且仅当x=0时等号成立,故f'(x)≥x-2ax=(1-2a)x,从而当1-2a≥0,即a≤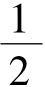 时,f'(x)≥0(x≥0),而f(0)=0,于是当x≥0时,f(x)≥0,
时,f'(x)≥0(x≥0),而f(0)=0,于是当x≥0时,f(x)≥0,
当a>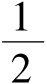 时,由ex>1+x(x≠0)可得e-x>1-x(x≠0),∴-x<e-x-1(x≠0),
时,由ex>1+x(x≠0)可得e-x>1-x(x≠0),∴-x<e-x-1(x≠0),
∴f'(x)<ex-1+2a(e-x-1)=e-x(ex-1)(ex-2a).
故当x∈(0,ln2a)时,f'(x)<0,而f(0)=0,于是当x∈(0,ln2a)时,f(x)<0与已知矛盾。
综上,a的取值范围为(-∞,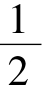 ]。
]。
通过对比,我们可以看出,命题者在命题时也是煞费苦心,考虑到文理生在同一个知识点上难度要求的差异,进一步体现理科生的思维特点,增加了放缩的技巧,提高题目的难度系数,适宜理科优秀人才的选拔。
例2(2004.全国I.理.22) 已知数列{an}中a1=1,且a2k=a2k-1+(-1)k,a2k+1 =a2k+3k.
(I)求a3,a5;(II)求{an}的通项公式.
【解答过程】(I)a2=a1+(-1)1=0,a3=a2+31=3,a4=a3+(-1)2=4,a5=a4 +32=13,所以,a3=3,a5=13.
(II)a2k+1=a2k+3k=a2k-1+(-1)k+3k,所以a2k+1-a2k-1=3k+(-1)k
同理,a2k-1-a2k-3=3k-1+(-1)k-1,……,a3-a1=3+(-1)
由累加法求得: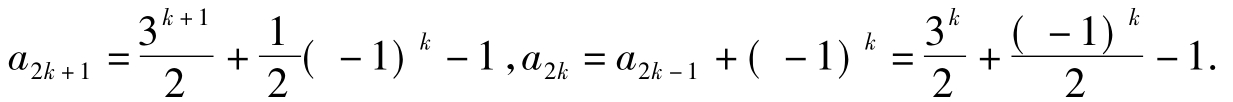 ∴当n为奇数时,
∴当n为奇数时,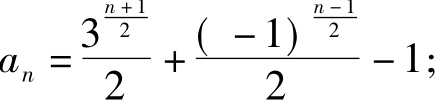 当n为偶数时,
当n为偶数时,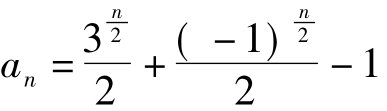
【点评】本小题主要考查数列,等比数列的概念和基本知识,考查运算能力以及分析、归纳和推理能力。
在数列中,但凡涉及到(-1)n问题往往是需要分奇偶讨论的,这样可以大大简化问题,各个突破。不过在分类解答时千万要记住,在不同的情形下,n的最小值是不同的。当n为偶数时,的最小值为2,有不少考生往往会误认为n的最小值总是1,导致最后不能获得正确答案。
例:若不等式 对任意的正整数n恒成立,求实数a的取值范围。
对任意的正整数n恒成立,求实数a的取值范围。
有不少考生认为当n为偶数时,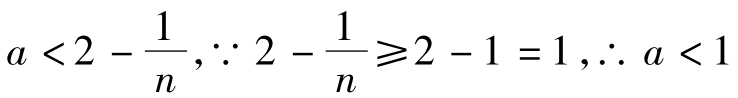 。其实不然,当n为偶数时,
。其实不然,当n为偶数时,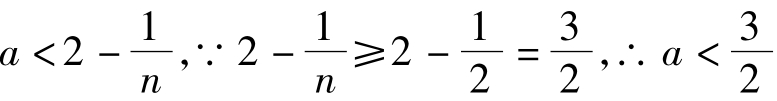 。在日常教学中,像这样的情况,会反复出现。只要善于总结,错误还是可以避免的。
。在日常教学中,像这样的情况,会反复出现。只要善于总结,错误还是可以避免的。
三、实际应用、创新考题考情的分析与研究
在新课程背景下,有关实际应用和创新考题越来越受重视,如何做到分类既不重复又没有遗漏是成功解决概率应用题的关键。在15分钟之内把一个复杂的问题考虑得不重不漏确实不是一件易事,一方面需要有完备概率知识,另一方还需有过硬的心理素质。
例(2010.安徽.理.21) 品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出n瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这n瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评分。
现设n=4,分别以a1,a2,a3,a4表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令X=|1-a1|+|2-a2|+|3-a3|+|4-a4|,则是对两次排序的偏离程度的一种描述。
(Ⅰ)写出X的可能值集合;
(Ⅱ)假设a1,a2,a3,a4等可能地为1,2,3,4的各种排列,求X的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有X≤2,
(i)试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ii)你认为该品酒师的酒味鉴别功能如何?说明理由。
【解答过程】由于1,2,3,4的排列有24种,要枚举这24个排列必须要按一定的原则进行分类排列,否则极易混乱。可以按1在首位、2在首位、3在首位、4在首位进行列表,共4种情况:
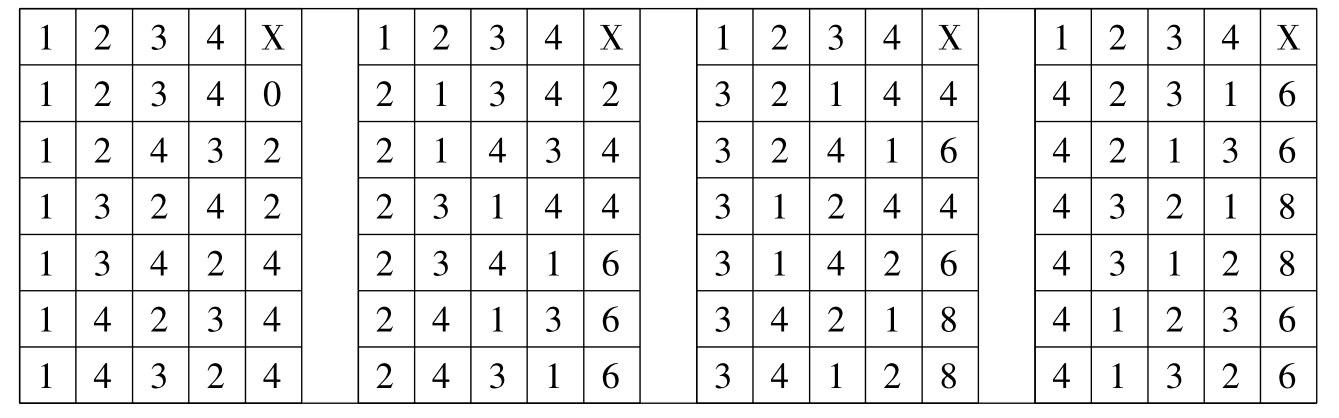
(Ⅰ)所以X的可能值集合为{0,2,4,6,8},其分布列如下:
(Ⅱ)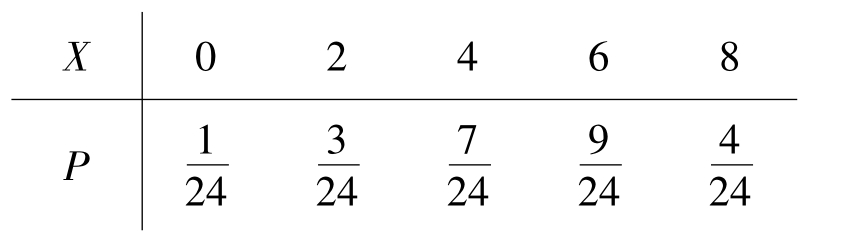
将三轮测试都有的概率记做p,由上述结果和独立性假设,得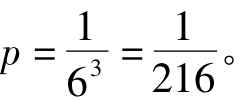
(ii)由于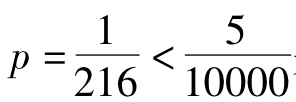 是一个很小的概率,这表明如果仅凭随机猜测得到三轮测试都有X≤2的结果的可能性很小,所以我们认为该品酒师确实有良好的味觉鉴别功能,不是靠随机猜测。
是一个很小的概率,这表明如果仅凭随机猜测得到三轮测试都有X≤2的结果的可能性很小,所以我们认为该品酒师确实有良好的味觉鉴别功能,不是靠随机猜测。
本题是考查离散型随机变量及其分布列,考查在复杂场合下进行计数的能力,通过设置密切贴近生产、生活实际的问题情境,考查概率思想在现实生活中的应用,考查抽象概括能力、应用与创新意识。该命题贴切生活实际,立意新颖,不仅要会计算概率,还需对概率有深刻的理解,能运用概率的知识指导生活实际,是难得一见的好题。
总之,分类讨论思想是一种“化繁为简、化整为零,分别对待、各个击破,再积零为整”的思维策略。这种思想对于简化研究对象,发展人的思维有着重要帮助。因此有关分类讨论的数学命题在高考试题中占有重要位置,我们绝不可以掉以轻心。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















