关注数学精神

课堂教学设计中需关注传递数学家的精神力量，以及需关注学生的探究精神、创新精神的培养。

例如：阁楼中的勇士

《费马大定理，一个困惑了世间智者358年的谜》中有这样一段介绍：“在世纪交替的时刻，有人问伟大的逻辑学家大卫·希尔伯特为什么他不去尝试证明费马大定理。他回答说：‘在开始着手之前，我必须花三年的时间做深入细致的研究，而我没有那么多时间去浪费在一件可能会失败的事情上。’怀尔斯清楚地知道，为了有希望找到证明，他必须全身心地将自己投入这个工作中。但是与希尔伯特不一样，他准备冒这个风险。他阅读了所有的最新杂志，然后反复地操练最新的技巧方法，直到它们成为他的第二本能为止。为了为将来的战斗收集必要的武器，怀尔斯花了18个月的时间使自己熟悉以前曾被用于椭圆方程和模形式的，以及从它们推导出来的全部数学。这些还是比较小的投资，要记住他全面地估计过，任何对这个证明的认真的尝试很可能需要10年的专心致志的努力。”

又如：一次无声的学术报告

《数学文化小丛书——同余式及其应用》中有这样一段介绍：

“在1644年，梅森认为267－1是素数。在以后的两百多年时间内，人们一直认为267－1是素数。但是1903年10月，在纽约的一次数学学术会议上，大家要求科尔教授作报告。科尔不说一句话，在黑板上计算出267－1的值，接着他又把以下两数193，707，721和761，838，257，287用竖式相乘，发现所得结果完全相同。这证明267－1不是素数！在沉寂片刻以后，全体到会者突然报以暴风雨般的掌声向他表示祝贺！这就是著名的‘一次无声的学术报告’。会后有人问他：‘为了证明这个结果，您花了多少时间？’他轻描淡写地答道：‘三年内的全部星期天。’（那时还没有发明电子计算机！）”

在我们日常课堂教学中也可以设计一些探究性问题，从而培养学生的探究精神、钻研精神。

探究性问题的设计未必需要兴师动众。我们只需在大处着眼，在小处着手就可以了。比如我们可以将课本或练习册上的一些问题做一些小小的改编，做一些探究性的小设计，或者增加一些探究性的追问，就能起到非常好的教学效果。长此以往，在日积月累中学生的探究习惯自然而然就形成了。

先举一例，对高二第二学期练习册第17页第6题的探究教学设计。

题目：已知直线l经过点P（1，2），且与两坐标轴围成的三角形面积为S。

当S＝3时，满足条件的直线有几条？（2条）

当S＝4时，满足条件的直线有几条？（3条）

当S＝5时，满足条件的直线有几条？（4条）

教师在讲解时可以将三小题融会贯通，从逆向的角度对该问题增加第（4）问：研究当S在什么变化范围内取值时，满足条件的直线有2条？3条？4条？

通过增加第（4）问，不仅体现了从特殊到一般的思维探索过程，而且相应的解题方法也从单一的解方程组的思想，过渡到转化、化归、数形结合等思想方法。不仅提升问题的层次性、提升问题的探究价值，也有助于落实教学中学生探究精神的培养。

我们再举一例，对高三练习册第2页第2题的教学设计。

题目：三个平面最多把空间分割成几个部分？并画图表示。

我们可以在讲解完原问题之后，进一步提出一个更一般化的问题：n个平面最多把空间分成几个部分？

先做一些铺垫：n条直线最多将平面分成几个部分？

因为平面到空间，很多结论或者方法都是可以进行类比的，所以设计这样一个铺垫。其作用是：为了解决一个比较复杂的三维空间问题，教会学生降维思考，先在二维空间，即平面内思考——n条直线最多将平面分成几个部分？

直线l1将平面分成S1＝2个部分；增加第2条直线l2，l2与l1有一个交点，该交点将l2分成2段，该2段把各自的区域一分为二，所以增加了2个区域；增加第n条直线ln，ln与前n－1条直线都相交，有n－1个交点，这些交点将ln分成n段，该n段把各自的区域一分为二，所以增加了n个区域，故我们有Sn＝Sn－1＋n（n≥2）。采用叠加法可得＋1。

在上述二维空间研究的基础上，再尝试研究三维空间，n个平面最多把空间分成几个部分？

设n个平面最多把空间分成Vn个部分。运用类比思想，列出下表：

让我们先来明确一下目的：1.先求出x；2.再求出Vn。

可将表中问题“这n－1条交线将平面αn最多分成x个隔膜。（即求x）”转化为“n－1条直线最多能将平面分割成几部分？”

由n条直线分平面的研究，得n条直线最多将平面分成＋1个部分，故n－1条直线最多能将平面分割成个部分，即这n－1条交线将平面αn最多分成个隔膜。这-个隔膜把各自的空间区域一分为二，所以增加了-个空间区域。

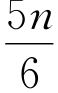于是得Vn＝Vn－1＋--＋1（n≥2），由叠加法可得＋1。

我们还可以进一步向学生提出问题：n个圆最多把平面分成几个部分？推广到空间：n个球最多把空间分成几个部分？

我想，这样设计的教学价值除培养学生的空间想象能力外，还体现在：巩固由递推公式求数列通项的叠加法；渗透平面到空间的类比思想；通过推广问题，培养学生追求数学一般规律的科学精神；培养学生研究性学习的意识、习惯与能力。

我们再来看一道2009年上海高考题：

某地街道呈现东—西、南—北向的网格状，相邻街距都为1。两街道相交的点称为格点。若以互相垂直的两条街道为轴建立直角坐标系，现有下述格点（－2，2），（3，1），（3，4），（－2，3），（4，5），（6，6）为报刊零售点。请确定一个格点（除零售点外）________为发行站，使6个零售点沿街道到发行站之间路程的和最短。

让我们来分析一下：

设应在格点（m，n）处建立发行站。

令y横向路程和＝2|m＋2|＋2|m－3|＋|m－4|＋|m－6|，

再令y纵向路程和＝|n－1|＋|n－2|＋|n－3|＋|n－4|＋|n－5|＋|n－6|。

下面的目的便是求出y横向路程和以及y纵向路程和分别在什么时候取到最小值。

为了研究该问题，我们可以为学生搭建思维脚手架，给出这样4个小题：

1.求y＝|x－1|＋|x－2|的最小值；

2.求y＝|x－1|＋|x－2|＋|x－3|的最小值；

3.求y＝|x－1|＋|x－2|＋|x－3|＋|x－4|的最小值；

4.求y＝2|x－1|＋|x－2|＋|x－3|的最小值。

先看第1题，求y＝|x－1|＋|x－2|的最小值。对于|x－1|＋|x－2|，通过画数轴，将|x－1|＋|x－2|理解成实数轴上，实数x所对应的点到1和2所对应的点的距离之和。

于是我们可以发现：

当x∈（－∞，1）时，|x－1|＋|x－2|＞1，

当x∈［1，2］时，|x－1|＋|x－2|＝1，

当x∈（2，＋∞）时，|x－1|＋|x－2|＞1，

所以，当且仅当x∈［1，2］时，原函数的最小值为1。

第2题，求y＝|x－1|＋|x－2|＋|x－3|的最小值。同样运用数形结合思想，通过画数轴来解决。对于|x－1|＋|x－2|＋|x－3|，先处理|x－1|＋|x－3|这部分，再处理|x－2|。

所以，当且仅当x＝2时，函数的最小值为2。

第3题，求y＝|x－1|＋|x－2|＋|x－3|＋|x－4|的最小值。

我们先处理|x－1|＋|x－4|这部分，通过数轴可以知道当且仅当x∈［1，4］时，它的最小值为3，再来处理|x－2|＋|x－3|这部分，通过数轴可以知道当且仅当x∈［2，3］时，它的最小值为1。

所以，当且仅当x∈［2，3］时，原函数的最小值为4。

第4题，求y＝2|x－1|＋|x－2|＋|x－3|的最小值。

我们将2|x－1|＋|x－2|＋|x－3|改写为这样的形式：

|x－1|＋|x－1|＋|x－2|＋|x－3|。

首先，让我们来处理|x－1|＋|x－3|这部分，通过画数轴，我可以得到，当且仅当x∈［1，3］时，它的最小值为2。接着，我们再来处理|x－1|＋|x－2|这部分。

于是，我们得到结论：当且仅当x∈［1，2］时，函数的最小值为3。

下面，我们来回到原问题，y横向路程和以及y纵向路程和分别在什么时候取到最小值。

所以，当且仅当m＝3时，y横向路程和取到最小值14。

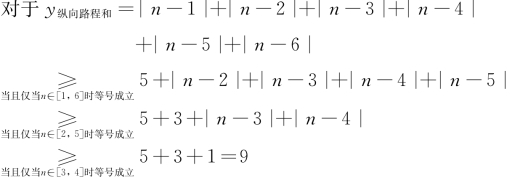
所以，当且仅当n＝3或n＝4时，y纵向路程和取到最小值9。

这样，我们有——当且仅当m＝3时，y横向路程和取到最小值14；当且仅当n＝3或n＝4时，y纵向路程和取到最小值9。可见发行站建立在（3，3）和（3，4）都行，而（3，4）是零售店，所以答案为（3，3）。

到此，我们为什么不趁热打铁，引导学生继续做更深入的探究呢？

我们可以因势利导，继续向学生抛掷以下两个问题。当然，如果学生能在问题一的基础上，自发地做推广，从而得到问题二，那就更好了。

问题一：求f（x）＝|nx－1|＝|x－1|＋|2x－1|＋…＋|2013x－1|的最小值。

问题二：求f（x）＝|nx－1|＝|x－1|＋|2x－1|＋…＋|n0x－1|（n0∈N*）的最小值。

分析问题一：

f（x）＝|x－1|＋|2x－1|＋|3x－1|＋…＋|2013x－1|

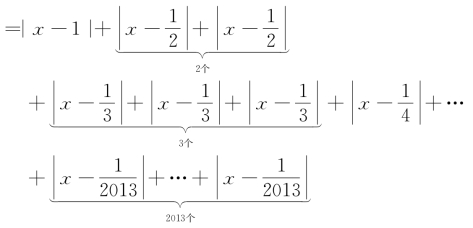
构造样本（共1＋2＋3＋…＋2013＝2027091个数）：

1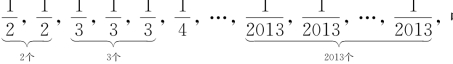，中位数xmd＝。

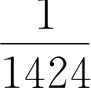所以，（f（x））min＝f（xmd）＝

分析问题二：

f（x）＝|x－1|＋|2x－1|＋|3x－1|＋…＋|n0x－1|

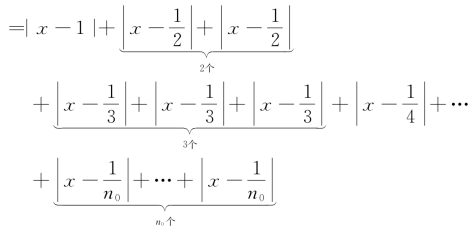
1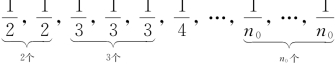，--，中位数记为xmd，

所以，（f（x））min＝f（xmd）＝|n·xmd－1|。

无论是数学概念的教学，抑或是习题的教学，我们随时都可以引导学生探究，令探究的精神深入骨髓。