第三节 一元二次方程概念[3]——HPM视角下的一则教学设计
一元二次方程这个课题蕴涵着丰富的历史文化信息,古代埃及、美索不达米亚、中国、印度、希腊和阿拉伯的数学文献中都有一元二次方程问题。然而,由于对有关历史知识缺乏足够的了解,人们在课堂教学中很少利用这些历史上的问题。
《全日制义务教育数学课程标准》(下简称《标准》)在“教材编写建议”中指出:“教材内容的编排和呈现要突出知识的形成和应用过程;应引导学生从已有的知识和经验出发,进行自主探索与合作交流……应关注对学生人文精神的培养。”“在数与代数部分,可以穿插介绍代数及代数语言的历史……也可以介绍……与方程及其解法有关的材料……”在“教学建议”中指出:“数学教学应从学生的实际出发,创设有助于学生自主学习的问题情境。”“在教学活动中,教师……要创造性地使用教材,积极开发、利用各种教学资源,为学生提供丰富多彩的学习素材。”数学史是数学教学的重要资源,数学史上的有关问题则是学生良好的学习素材。
考察一元二次方程的历史,我们发现,最早出现的一元二次方程是x2=A,而学生此前已经学过平方根知识,因此,教学设计时可以从这类问题入手。

图2-3-1 埃及吉萨金字塔
教师可先展示图2-3-1,并自然地引入主题。
看到这高耸入云霄的金字塔,我们一定会联想到遥远的古埃及文明。生活在尼罗河两岸的古埃及人创造了世界上最早的数学文化,这种文化的载体是他们使用的纸草书。在俄罗斯首都莫斯科的普希金艺术博物馆里,收藏有制作于约公元前1850年、公元1893年购自埃及的珍贵的纸草书,长约18英尺,宽约3英寸(展示图2-3-2)。在纸草书上的25个数学问题中,有一个问题是这样的:
例1 矩形面积为12,宽为长的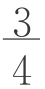 。问该矩形的长、宽各为多少?
。问该矩形的长、宽各为多少?
教师让学生解这一古老的数学问题。
从历史上看,古代巴比伦人的许多数学问题都可归结为方程组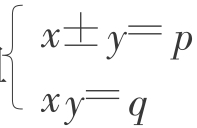 的求解。如:“矩形的长比宽多7,面积为60。问长、宽各多少?”“一个正方形面积减去它的边长,差为870。求边长。”这类问题在其他地区的数学史上也屡见不鲜。如欧几里得的《几何原本》卷二中的问题:“将一条线段分成两部分,使整段与其中一分段构成的矩形面积等于另一分段上的正方形面积”;我国北宋时代数学家刘益在《益古根源》中解决了如下问题:“直田积864步,只云阔不及长12步,问长几何。”“直田积864步,只云长阔共60步,欲先求阔步,问得几何。”
的求解。如:“矩形的长比宽多7,面积为60。问长、宽各多少?”“一个正方形面积减去它的边长,差为870。求边长。”这类问题在其他地区的数学史上也屡见不鲜。如欧几里得的《几何原本》卷二中的问题:“将一条线段分成两部分,使整段与其中一分段构成的矩形面积等于另一分段上的正方形面积”;我国北宋时代数学家刘益在《益古根源》中解决了如下问题:“直田积864步,只云阔不及长12步,问长几何。”“直田积864步,只云长阔共60步,欲先求阔步,问得几何。”
在学生得出矩形的长为4之后,教师先展示图2-3-3,接着引入新的矩形面积问题。
现在大家看到的是另一个文明古国的遗物——巴比伦泥版。古代巴比伦人的代数水平比埃及人更高,解决的代数问题更复杂。在美国耶鲁大学所收藏的巴比伦泥版中,有一块上面记载着如下问题:
例2 已知矩形面积为60,长比宽多7。问该矩形的长为多少?列出矩形的长所满足的方程。
接着教师可以把上述问题的条件稍改一下,得另一富有巴比伦特色的问题:
例3 已知矩形面积为60,长宽之和为17,问该矩形的长为多少?列出矩形的长所满足的方程。

图2-3-3 巴比伦泥版

图2-3-4 斐波纳契
《标准》在“教材编写建议”中以“梯子问题”为例说明如何体现数学知识的形成与应用过程:“一个长为10米的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8米。如果梯子的顶端下滑1米,那么(1)猜一猜,底端也将滑动1米吗?(2)列出底端滑动距离所满足的方程。”其实,这类问题在历史上有很多。表2-3-1列出了典型数例。
表2-3-1
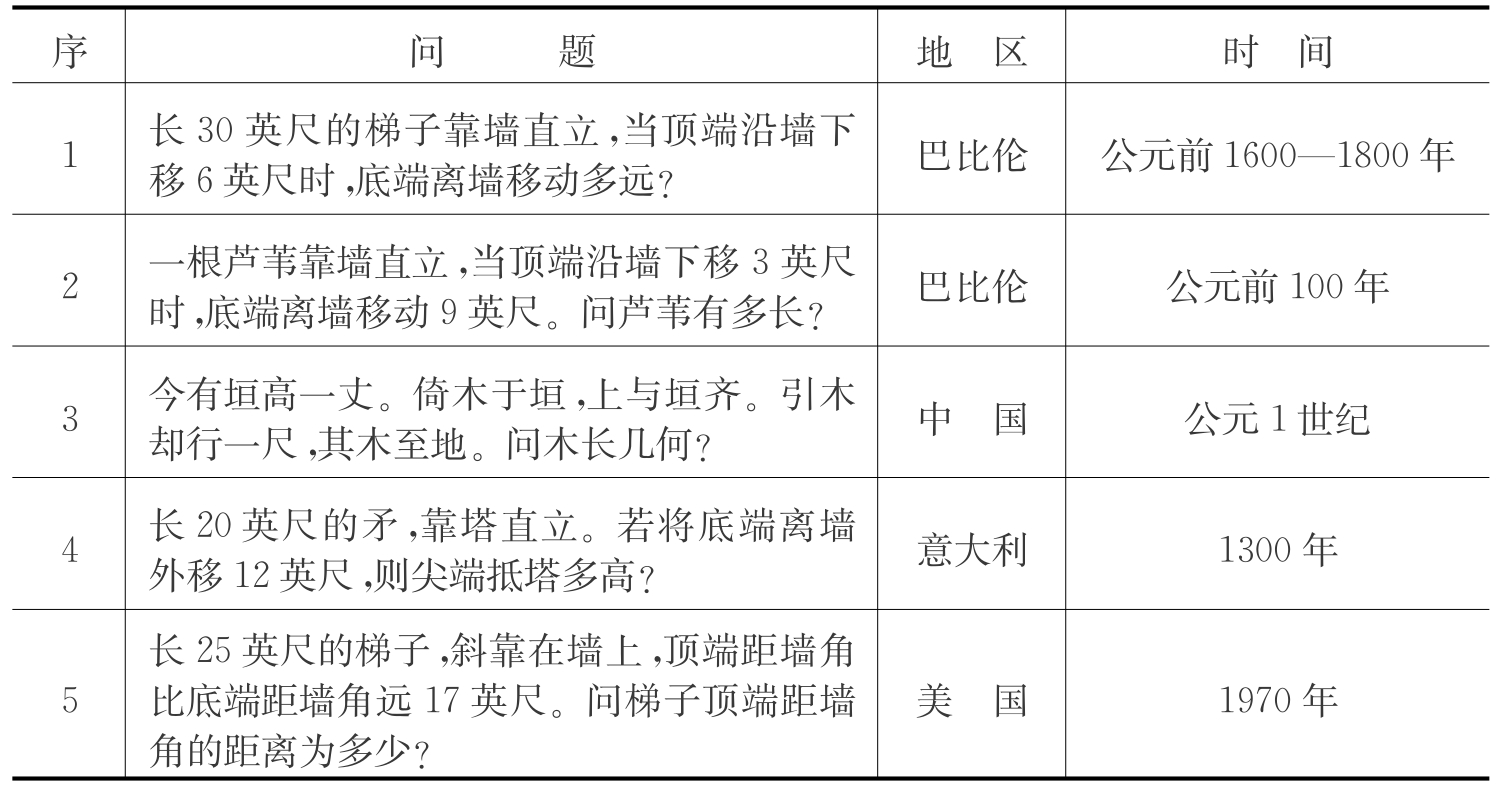
表2-3-1中前四问均可利用勾股定理通过直接开方或解一元一次方程得出答案,第五问需用一元二次方程来求解。据此教师可以进一步设置新的一元二次方程问题。
巴比伦人很早就知道勾股定理,图2-3-3就是一个已知正方形边长为30,求对角线的问题。实际上,在巴比伦泥版上,有关勾股定理的应用题相当多。下面的“梯子问题”便是其中之一。
例4 长为30英尺的梯子竖直靠在墙上,当梯子的顶端沿墙向下滑动6英尺时,底端离墙滑动多远?
在学生获得答案之后,教师进一步给出下面的问题让学生解答。
例5 在例3中,如果梯子的顶端沿墙再一次向下滑动6英尺,那么底端将再一次滑动多远?试列出底端再一次滑动的距离所满足的方程。
历史上许多测量问题可用一元二次方程来解,如《九章算术》勾股章中的问题:“今有邑方不知大小,各中开门。出北门二十步有木,出南门一十四步,折而西行一千七百七十五步见木。问邑方几何?”
由于学生已经学过三角形的相似性,故教学设计时可以采用这个古老的问题,毕竟,它是中国数学史上第一个一元二次三项方程!以下是根据“邑方问题”改编的问题。
例6 如图2-3-5所示,有一所正方形的学校,南门和北门各开在南、北面围墙的正中间。在北门的正北方20米处有一棵大榕树。一个学生从南门出来,朝正南方走14米,然后转向西走1775米,恰好见到学校北面的大榕树。问这所学校每一面围墙的长度是多少?试列出方程。
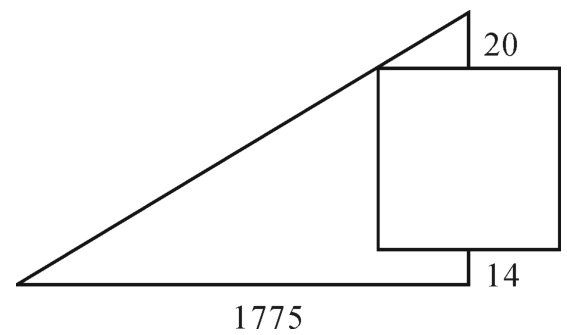
图2-3-5
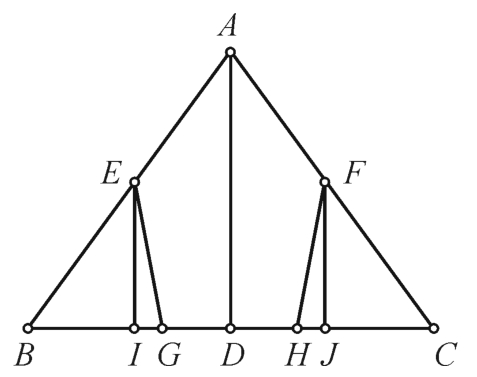
图2-3-6
《标准》在“教学建议”中指出:“教学中应当有意识、有计划地设计教学活动,引导学生体会数学之间的联系,感受数学的整体性,不断丰富解决问题的策略,提高解决问题的能力。”数学史上的问题在这方面也是大有作为的。如,教师可以给出中世纪意大利数学家斐波纳契(L.Fibonacci,1175—1250)在其名著《花朵》中提出的几何问题,说明几何与代数之间的密切联系。
(展示图2-3-4)现在大家看到的是中世纪欧洲最伟大的一位数学家,他叫斐波纳契。他在1225年写成一本书,叫《花朵》(听起来不像数学书名)。在这本书中,斐波纳契提出了如下问题:
例7 如图2-3-6所示,在等腰三角形ABC中,已知AB=AC=10,BC=12。AD是底边BC上的高。在AB、AC上各求一点E、F,在BC上求两点G和H,使得AEGHF是等边五边形。
这样,在教师的引导下,基于已有的知识和经验,学生从例2、例3、例5、例6、例7中分别得到各不相同的一元二次方程,如表2-3-2所示。
表2-3-2
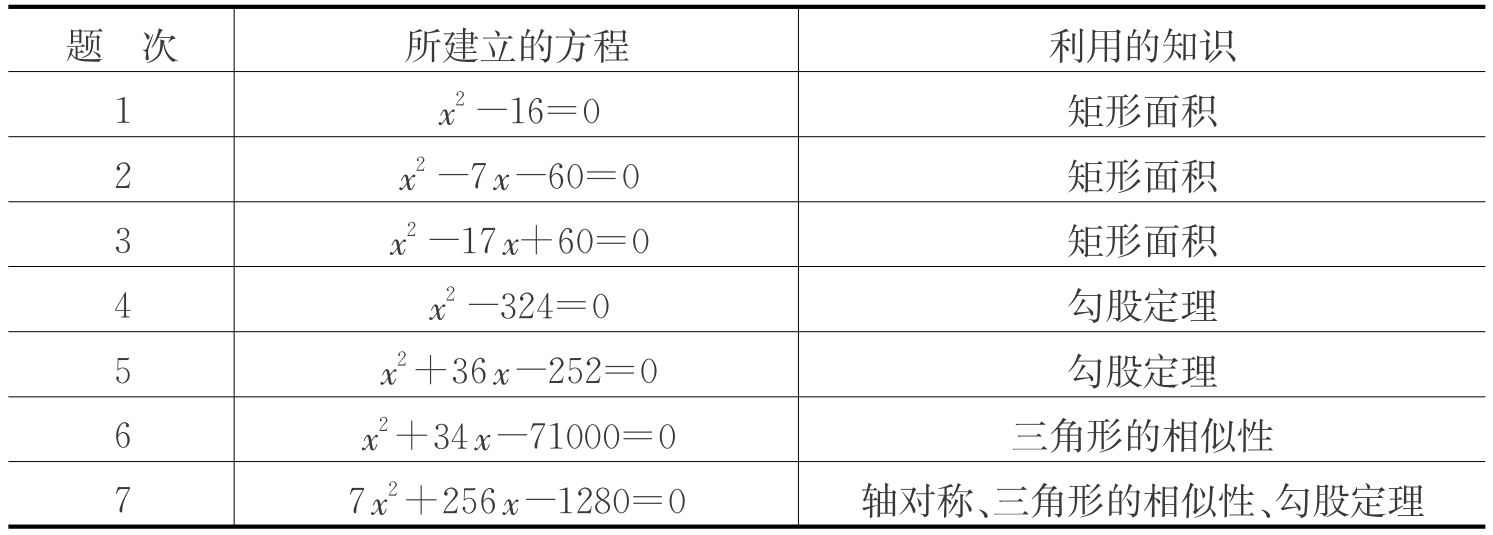
接下来,教师让学生观察这些方程的共同特征,提炼出一元二次方程的概念。
课堂练习也可以采用数学史上的问题。如:
练习1 两个正方形面积之和为1000。一个正方形边长是另一正方形边长的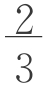 减去10。求这两个正方形的边长。(巴比伦泥版上的问题)
减去10。求这两个正方形的边长。(巴比伦泥版上的问题)
尽管上面这类问题在历史文献中也有不少,如斐波纳契《计算之书》第15章中即有“将10分成两部分,使它们的平方和为62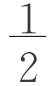 ”、“将12分成两部分,使其中一部分的平方等于另一部分的27倍”等一元二次方程问题,但《标准》在教学建议中指出:“抽象数学概念的教学,要关注概念的实际背景和形成过程”,在教材编写建议中又指出:教材应“围绕所要学习的数学主题,选择有意义的、对学生具有一定挑战性的、能够表现重要数学意义、有利于学生一般能力发展的内容”,因此,我们在教学设计中,当然不能仅仅选择这类缺乏实际背景的问题。
”、“将12分成两部分,使其中一部分的平方等于另一部分的27倍”等一元二次方程问题,但《标准》在教学建议中指出:“抽象数学概念的教学,要关注概念的实际背景和形成过程”,在教材编写建议中又指出:教材应“围绕所要学习的数学主题,选择有意义的、对学生具有一定挑战性的、能够表现重要数学意义、有利于学生一般能力发展的内容”,因此,我们在教学设计中,当然不能仅仅选择这类缺乏实际背景的问题。
历史上,公元9世纪阿拉伯数学家花拉子米(Al-Khwarizmi,783—850)在其名著《代数学》中,给出过一元二次方程x2+10x=39的两种几何解法,如图2-3-7和2-3-8所示。图2-3-7中,中间正方形边长为x,四角的小正方形边长为5/2;图2-3-8中,左上正方形边长为x,右下正方形边长为5。这就是解一元二次方程的配方法的两种几何模型,对于后面的教学有重要意义。受这个模型启发,我们可以设计下列问题。
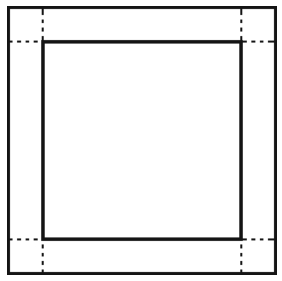
图2-3-7
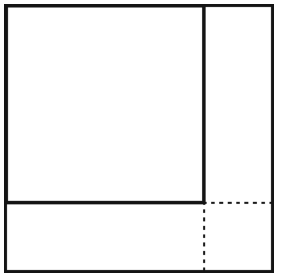
图2-3-8
练习2 在某公园内一块边长为50米的正方形空地上建造一个正方形鱼池,要求水池旁边有供人观赏行走的通道,且水池占地面积为空地面积的60%。请完成你的设计。
本教学设计在以下几个方面贯彻了数学新课程的思想、理念、目标和要求。
包含浓郁的历史文化气息,体现数学是人类的一种文化。让学生体会数学的悠久历史,数学与人类文明的密切相关性,数学文化的多元性。
教学活动建立在学生已有的知识经验基础之上,在引出新知识的同时也巩固了旧知识(如开平方、轴对称、勾股定理、图形的相似性等)。
增强学生的应用意识,让学生体会数学与现实生活的联系。
使学生经历从实际问题中建立数学模型的过程,感受一元二次方程作为一种数学模型的重要性。
使学生经历数学知识的形成过程。
利用背景知识以及古人的问题情境,激发学生的好奇心与学习兴趣,促进自主学习。
使学生体会到不同数学知识之间的密切联系。
创造学生的学习动机,为后面一元二次方程解法的教学埋下了伏笔。
本教学设计并未经过课堂实践检验,也没有照搬的必要。笔者只是想利用这一设计说明:HPM(数学史与数学教学关系)为中学数学教学的设计提供了一个新视角,这种视角下的数学教学完全能很好地贯彻数学新课程的思想和理念,完成或达到新课程的目标和要求;同时,在实现情感与态度目标方面,它必将显示出一定的优势。
[1]教育部.全日制义务教育数学课程标准(实验稿)[M].北京:北京大学出版社,2001.
[2]Eves H.An Introduction to the History of Mathematics[M].Philadelphia:Saunders College Publishing,1983:36-43.
[3]McM illan R D.Babylonian quadratics[J].Mathematics Teacher,1984,77:63-65.
[4]汪晓勤.历史数学问题札记[J].中学教研(数学),2004(1).
[5]汪晓勤,黄芳.巴比伦泥版文献中的勾股定理[J].中学教研(数学),2003(2).
[6]汪晓勤.斐波纳契是如何解方程的?[J]数学传播,2005,29(1):51-63.
[7]Siegler L E.Fibonacci's Liber Abaci:A translation into modern English of Leonardo Pisano's Book of Calculation[M].New York:Springer-Verlag,2002.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














