消费者个人的满足

第一节　消费者个人的满足

人类幸福最根本的特征是，人追求心理满足的天性以及人关于幸福的实际体验与直觉感受。实际体验与直觉感受的程度取决于消费者个人所消费的东西。效用是对消费者个人从商品和服务的消费中所能够获得的满足程度的度量。因此，主流经济学家认为：理性人的幸福即是在约束条件下最大化自己的效用。那么，在个人追求幸福这个终极目标之下，我们首先要学习一下效用理论。

一、效用理论

效用理论在经济学中具有极端重要的地位。培根（Francis Bacon）说过：“史鉴使人明智。”因此，还是有必要花费一些时间回顾一下效用理论的历史变迁。

1.效用理论的历史变迁

从亚里士多德的《政治学》首次出现“效用”一词，经过一代一代传播，1738年，瑞士的伯努里（D.Bernoulli）在其《测定风险新理论之解说》一文中指出：一物的价值是以其带来的效用为基础的。一物的效用取决于评价该物的人的特殊情况。“一千元的收益对于一个穷人比对一个富人无疑具有更大的意义。”

意大利的加里阿尼（F.Galiani）在其1750年出版的《货币论》中指出：效用是一物带来福利的能力。人是由各种情欲构成的，这些情欲以一种合力推动着他。情欲的满足是享乐，享乐的获得是福利。

斯密在《国富论》里，把“效用”作为一种客观意义上的“有用性”等同于商品的“使用价值”。“效用”作为一种主观心理概念则追溯到斯密《国富论》之前的《关于法律、警察、税收及军备的演讲》一书。

边沁在研读斯密《国富论》的基础上，在1780年出版的《道德与立法原理导论》第一版中指出：效用是事物具有为人带来利益、便利、快乐、好处、幸福，或者，避免损失、妨碍、痛苦、不幸的能力。^[1]边沁认为，经济学应以最大化幸福原理和效用原理为基础，同时，他还提出了效用递减法则。

德国的戈森（H.Gossen）在1854年出版的《人类交换规律与人类行为准则的发展》中提出了效用变化法则，该法则被称作“戈森第一定律”。

在边沁的效用观的基础上，杰文斯1871年出版了《政治经济学理论》，首先发现并肯定了戈森的效用变化法则，与门格尔、瓦尔拉一起领导了“边际革命”，完全从主观感受的角度解释效用，并提出了边际效用递减规律。杰文斯认为：凡是能引起快乐或避免痛苦的东西都可能有效用。效用是事物以某种方式服务于人类的能力。进一步地，他认为：效用虽是事物的一种性质，但不是事物的内在性质，它最好被看作是事物的一种情况，即事物与人的需求关系引起的情况。为此，效用的有无或变化，都是以事物与人的需求之间的关系而转移的。

新古典经济学一直把效用比作物理学中的能量。^[2]埃奇沃思在其1881年出版的《数学心理学》中指出：物理研究的主要目标是能量的累积或时间的积分。与此类似，快乐的累积是通过每一时刻的快乐或效用相加而成的时间的积分。^[3]

奥地利的庞巴维克（E.V.Bohm-Bawerk）在其1884年出版的《资本与利息》中指出：人的欲望及其满足是一切经济活动的出发点，因而也是价值论的出发点。物品能满足人的欲望的性质就是物品的效用。效用即欲望的满足，它是主观的。

关于效用的人际比较问题，门格尔和瓦尔拉都认为毫无困难。马歇尔1890年出版的《经济学原理》，完全接受了基数效用理论，指出：效用如果不能在人与人之间进行比较，那么，肯定可以在集群之间进行比较。20世纪30年代，大多数经济学家在效用的人际比较以及如何衡量的问题上，感到越来越不满意。1934年，希克斯与艾伦的撰文《价值理论的再思考》，对满足也仅进行了序数比较。^[4]

值得注意的是，在古典和新古典经济学文献中，效用的外延较为宽泛，既可以描述人的物质追求，也可以描述人的精神追求。例如，穆勒、杰文斯和马歇尔等人阐述效用时，都十分自然地提到人对尊严、荣誉、自豪感、成就感甚至道德感的追求。这是一种广义的效用范式。在现代经济学文献中，效用被定义为“一个人从消费一种物品或服务中得到的主观上的享受和有用性”^[5]，其外延日趋狭窄。这种狭义的效用范式引起当代经济学家的批判。

2.效用的概念

“效用”一词可概括为行为主体在实现自身需要的任一行为过程中所获得的心理或生理上的满足状态。对消费者个人而言，我们可以从消费的主体与消费的客体两个方面讨论效用。从消费的主体来讲，效用是消费者个人从自身消费行为中得到的满足；从消费的客体来讲，效用是商品满足人的欲望或需要的能力。

显然，这是一个把经济现象与心理现象联系、融合在一起的心理物理概念，也是把心理学分析引入经济现象的结果。

需要说明的是：

（1）效用是一个相对概念，只有在同一物品的前后满足程度之间或不同物品的满足程度之间相互比较时才有意义。

（2）效用有无或效用大小取决于个人主观心理评价。同一物品有无效用或效用大小，对不同的人来说是不同的。

（3）效用本身不具有伦理学意义。一种商品是否具有效用，要看它是否能满足人的欲望或需要，而不涉及这一欲望或需要的好坏。例如，吸毒从伦理上讲是坏欲望，但毒品能满足这种欲望，因此它具有这种效用。

（4）与效用概念意义相反的概念是负效用，是指某种东西所具有的引起人的不舒适感或痛苦的能力，如失恋的打击等。

（5）同一物品对于不同的人的效用是不同的。因此，除非给出特殊的假定，否则效用是不能在不同的人之间进行比较的。例如，辣椒对于有此偏好的人来说，其效用是很大的，反之则很小甚至为0。

3.效用函数

主流经济学把消费者个人抽象为一个“黑箱”，以一个幸福方程式、幸福函数即效用函数来代替消费者个人而不理会其内部结构与生理机制，仅分析消费者个人消费的商品（投入）与其获得的满足（产出）之间的关系。^[6]

函数是因果关系的数学形式。效用函数就是关于消费者个人的幸福即效用与其主要影响因素之间因果关系的数学表达形式。

“效用”是人的需要所获得的满足状态。需要层次理论提出人类经济活动的最终目的是满足自身的需要，而人的需求偏好是复杂多样的，影响人类生存和发展的因素都会影响其需求偏好。

事实上，贝克尔在研究家庭经济行为时提出的“扩展的效用函数”（extended utility function），^[7]阿玛蒂亚·森提出的把道德变量引入现代福利经济学的“复合效用”（plural utility），^[8]澳大利亚莫纳什大学黄有光（Yew-Kwang Ng，1943—　）的“快乐理论”^[9]等，都从不同层面、不同角度触及效用的广义性质。就是说，人类追求的幸福目标是一个多元的效用函数。

埃奇沃思在1881年的《数学心理学》中研究的就是人的幸福的计算，并把效用看作是所有商品的一般函数。^[10]贝克尔也构造了如下的个人效用函数：

其中，z₁，z₂，…，z_m是满足对应基本欲望的商品的数量。

在第一章已讲过，主流经济学家几乎是把“需要”与“欲望”并列使用的，就是说，可以用“需要”代替“欲望”。“需要”的完整形式包括生理的需要、安全的需要、交往的需要、尊重的需要、自我实现的需要五种。根据第一章的结论，可以把式（3.1）表示的贝克尔的个人效用函数中的变量归类成z₁，z₂，z₃，z₄，z₅这样5个。假设满足消费者个人完整“五个层次”需要的商品Z₁，Z₂，Z₃，Z₄，Z₅的消费量分别为z₁，z₂，z₃，z₄，z₅，则消费者个人的效用函数可有如下形式：

既然效用是用来表示消费者个人在消费商品时所感受到的满足程度的，于是，就产生了对这种“满足程度”即效用或幸福的度量问题。在这一问题上，主流经济学家先后提出了基数效用（cardinal utility）和序数效用（ordinal utility）的概念，并在此基础上，形成了分析消费者个人行为的两种方法，它们分别是基数效用论者的边际效用分析方法和序数效用论者的无差异曲线分析方法。

二、基数效用论与边际效用递减：一种产品效用的表现方法

在19世纪和20世纪初期，西方经济学家普遍使用基数效用的概念。基数效用论者认为，效用如同长度、重量等概念一样，可以具体衡量并加总求和，具体的效用量之间的比较是有意义的。表示效用大小的计量单位被称作效用单位。例如，对某一个人来说，吃一顿丰盛的晚餐和看一场高水平的足球赛的效用分别为5效用单位和10效用单位，则可以说这两种消费的效用之和为15效用单位，且后种效用是前种效用的2倍。

1.总效用

总效用（total utility，简称为U^[11]），是指消费者个人在一定时间内，消费一定数量的某一种商品，所得到的效用量的总和。随着消费量的增加，消费者个人获得的总效用也在不断地增加。总效用概念的理论依据是埃奇沃思、费雪基于物理学能量原理的“效用的积分”。

需要注意的是，第二章里我们已经讲过，商品之间的联系是普遍的，即商品之间存在着替代与互补的关系，一种商品会有其替代品和互补品。消费者个人消费一种商品所获得的总效用，会因为替代品而减少，会因为互补品而增加。

比如，日常生活中，人仅仅吃主食或者仅仅吃菜，获得的满足程度都是不高的，甚至不吃菜就吃不下饭。然而，饭菜搭配，则吃得也多，满足水平也高。一般形容说：“吃好了！酒足饭饱啊！”就是说，饭与菜是互补性的商品。再比如，茶水和白开水是替代品。仅有茶水或者白开水，人能够分别获得解渴的满足。但是，当同时有茶水和白开水时，偏好一种商品的人从另一种商品中获得的效用满足就会减少。

当然，此处介绍总效用的概念，是关于效用表现方法的开始，为了分析的由浅入深，我们先假设仅消费“某一种商品”，即假设的前提是商品之间的效用互不影响。

假定消费者个人消费一种商品Q^[12][13]的数量为q^[14]以获得效用或体验幸福，则总效用函数就有如下形式：

2.边际效用与边际效用递减规律

边际效用（marginal utility，简称M U）是指消费者个人在现有财富条件下，每增加一个单位商品和服务的消费所带来的总效用的变化或增量，或者说，增加最后一个单位商品和服务的消费所带来的效用的变化或增量。

依据式（3.3），边际效用为：

当商品的增加量趋于无穷小，即Δq→0时有：

边际效用递减规律（1aw of diminishing marginal utility）是指，在一定时间内，在其他商品的消费数量保持不变的条件下，随着消费者个人对某种商品消费量的增加，消费者个人从该商品连续增加的每一消费单位中所得到的效用增量即边际效用是递减的。

据基数效用论者解释，边际效用递减规律成立的理论依据是戈森第一定律和韦伯—费希纳定律，即可以是由于随着相同消费品的连续增加，从人的生理和心理的角度讲，从每一单位消费品中所感受到的满足程度和对重复刺激的反应程度是递减的；还可以是由于在一种商品具有多种用途时，消费者个人总是将第一单位消费品用在最重要的用途上，第二单位消费品用在次重要的用途上，等等。这样，消费品的边际效用便随着消费品的用途重要性的递减而递减。

通常被用来证明该规律的例子如下：在一个人很饥饿的时候，吃第一个包子给他带来的效用是很大的。以后，随着这个人所吃的包子数量的连续增加，虽然总效用是不断增加的，但每一个包子给他所带来效用增量却是递减的。当他完全吃饱的时候，包子的总效用达到最大值，而边际效用却降为零。如果他还继续吃包子，就会感到不适，这意味包子的边际效用进一步降为负值，总效用也开始下降。

3.一种商品的效用曲线

假设消费者个人消费一种商品Q的数量为q，同时假设这一种商品的效用U不受其他相关商品的影响。

消费者个人消费商品的数量是物理量，是可以触摸或感受到的量；消费者个人从消费的商品中获得的效用是一种心理量，是一种主观的评价。从消费者个人消费到满足，显然隐含着消费量（物理量）到效用或幸福（心理量）的转换问题^[15]，也就是斯密关心的“财富—幸福的转换问题”。现在人们称此为“幸福的技术”，以类似于下一章要讲的“生产技术”。

依据总效用的概念可知，随着消费者个人消费量（物理量）的增加，其总效用水平（心理量）增加。根据边际效用递减规律可知，每增加一个单位商品和服务的消费所带来的总效用的增量是递减的。因此，我们可以描绘出如图3.1和图3.2所示的一种商品的总效用曲线和边际效用曲线。总效用曲线U凹向横轴。

总效用曲线和边际效用曲线的描绘也可通过直接经验观察来进行。以某人消费橙汁为例，橙汁的消费量（物理量）与效用（心理量）和边际效用之间的关系，可有表3.1的情况。

表3.1　橙汁的效用表

由表3.1的第（1）、（2）和（3）栏可见，当商品的消费量由0增加为1时，总效用由0增加为10效用单位，总效用的增量即边际效用为10效用单位（因为10－0＝10）。当商品的消费量由1增加为2时，总效用由10效用单位上升为18效用单位，总效用的增量即边际效用下降为8效用单位（因为18－10＝8）。依此类推，当商品的消费量增加为6时，总效用达最大值为30效用单位，而边际效用已递减为0（因为30－30＝0）。此时，消费者个人对商品的消费已达到饱和点。当商品的消费量再增加为7时，边际效用会进一步递减为负值即－2效用单位（因为28－30＝－2），总效用便下降为28效用单位了。

根据表3.1所绘制的总效用曲线和边际效用曲线，也有如图3.1和图3.2所示的情形。

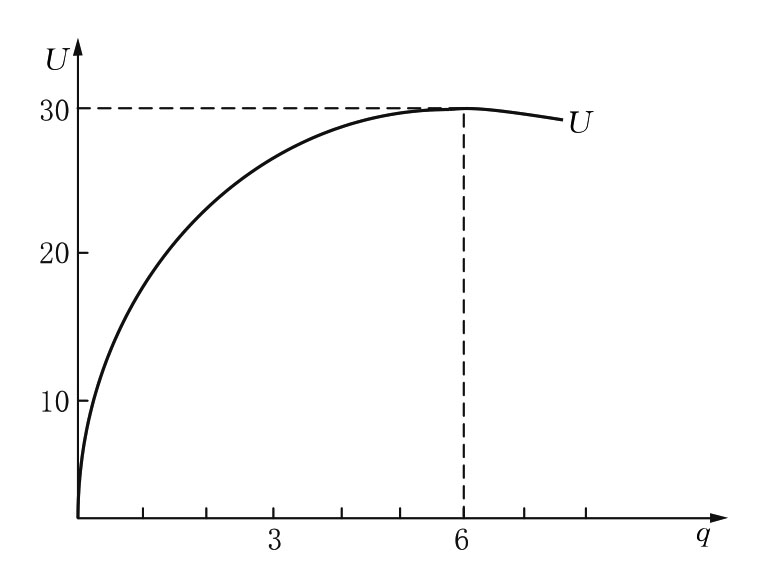
图3.1　一种商品的效用曲线

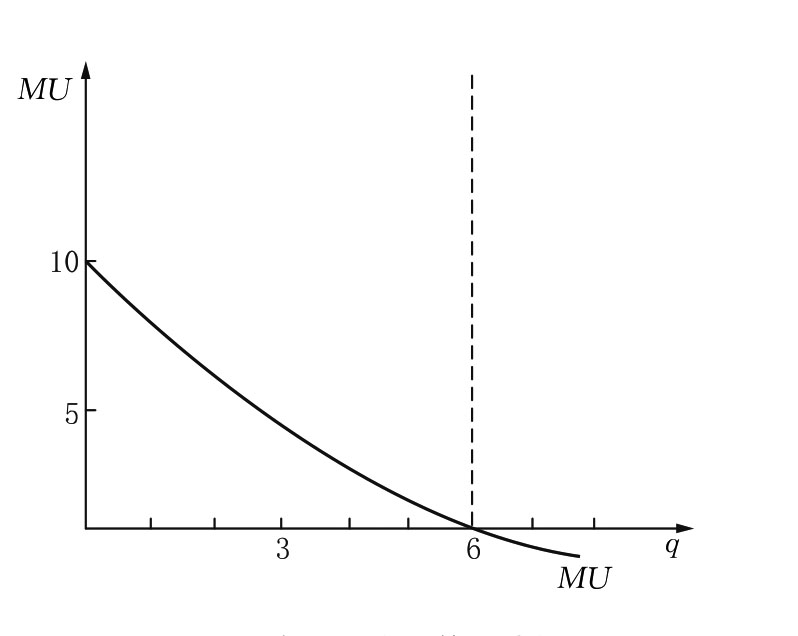
图3.2　商品的边际效用曲线

图3.1、图3.2中的横轴表示商品的数量，纵轴表示效用量，U曲线和MU曲线分别为总效用曲线和边际效用曲线。由于边际效用被定义为消费品的一单位变化量所带来的总效用的变化量，所以MU曲线上的每一个值都记在相应的两个消费数量的中点上。

在图3.2中，MU曲线是向右下方倾斜的，它反映了边际效用递减现律，相应地，U曲线是以递减的速率先上升后下降的。当边际效用为正值时，总效用曲线呈上升趋势；当边际效用递减为零时，总效用曲线达最高点；当边际效用继续递减为负值时，总效用曲线呈下降趋势。从数学意义上讲，如果效用曲线是连续的，则每一消费量上的边际效用值就是总效用曲线上相应的点的斜率。这一点，也体现在边际效用的定义公式（3.4）中。

边际效用递减规律，也可以用数学语言来表达：

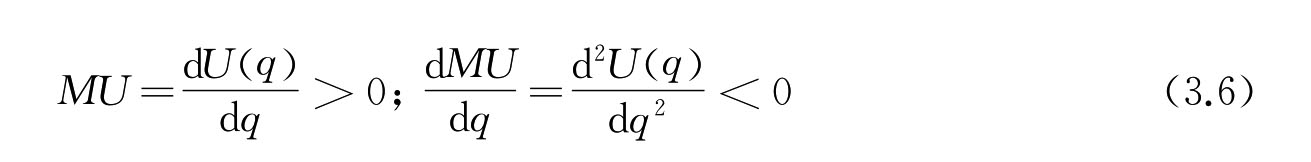
效用函数的一阶导数即边际效用大于零，表示随着q的增加，总效用也相应增加；效用函数的二阶导数小于零，则表示随着q的增加，边际效用是递减的。

三、序数效用论与等效用曲线：两种产品效用的表现方法

1934年希克斯与艾伦的著名论文提出：效用作为一种心理现象是无法计量的，因为不可能找到效用的计量单位。人们同时消费多种商品。比如，实际生活中，人不可能只消费一种商品，比如说只吃主食不吃菜，只追求精神享受不讲求物质满足。商品之间是普遍联系的，一般具有替代或互补关系。^[16]因此，消费者个人在市场上所做的并不是权衡商品效用的大小而只是在不同的商品之间进行排序，这就是所谓的序数效用论。

序数效用论者认为，商品的效用只能用顺序或等级来表示。他们提出消费者偏好的概念，取代了基数效用论者的关于效用的大小可以用“效用单位”来表示的说法。

1.消费者偏好

序数效用论者指出：消费者个人对于各种不同的商品组合的偏好（即爱好）程度是有差别的，这种偏好程度的差别决定了不同商品组合的效用的大小顺序。具体地讲，对于A、B两个商品组合，若某消费者个人对A组合的偏好程度大于对B组合的偏好程度，则可以说A组合的效用水平大于B组合，或者说，A组合给消费者个人带来的满足程度大于B组合。

序数效用论者对消费者偏好的分析基于以下假设条件：

（1）偏好具有完备性，即消费者个人能够按照其偏好而对所有可供选择的商品组合进行排序。例如，对于任何两个商品组合A和B，消费者个人总是可以做出，而且也仅仅只能做出以下三种判断中的一种：对A的偏好大于对B的偏好，对A的偏好小于对B的偏好，对A和B的偏好相同。对A和B具有相同的偏好，也被称作为A和B是无差异的。

（2）偏好具有传递性，即消费者个人能够以无矛盾的方式在各种可供选择的商品组合中进行选择。例如，对于任何三个商品组合A、B和C，如果某消费者已经做出判断：对A的偏好大于（或小于、等于）对B的偏好，对B的偏好大于（或小于、等于）对C的偏好。那么，该消费者必须做出对A的偏好大于（或小于、等于）对C的偏好的判断。

（3）偏好满足“无餍足”公理，即如果两个商品组合的区别仅在于其中一种商品的数量的不同，那么，消费者个人总是偏好于含有这种商品数量较多的那个组合。这意味着，消费者个人对每一种商品的消费都处于饱和以前的状态。

2.等效用曲线

第一章里讲过，消费者个人消费满足整体的“五个层次”需要的商品。商品之间的效用是相互影响的。要分析五种商品的效用是相当复杂的。事实上，两种商品足以表达全部商品，因为可以把其中的一种商品看作其他所有的商品。^[17]这似乎过于抽象。其实，过去的教材中经常使用“大炮—黄油”这个两商品模型，与我国西汉时期桓宽所著的《盐铁论》类似，分别代表满足人的安全需要的商品和生理需要的商品。如今，这模型被进一步完善成了“面包—电影”这样的两商品模型，分别表示人为了追求幸福这个终极目标而追求自己整体的“物质需要”和“精神需要”满足的两类商品。这就是说，可以从现实经济中抽象出用两种商品代表消费者个人消费的全部商品。

两种商品足以反映出商品之间的替代关系或互补关系。仍然举例饭与菜这两种商品。前已述及，饭与菜是互补的。但是，因为一个人的饭量有限，多吃菜就少吃饭，多吃饭就少吃菜，饭与菜又具有替代关系。当然，替代是有限度的。尽管有人试图通过只吃菜不吃饭来减肥，实际上这有损健康！从更一般意义上讲，人需要同时消费物质商品与精神商品，两种商品互补，人才能幸福快乐。但是，物质商品与精神商品也具有替代关系，因为任何人的财富收入在一定时期内都是稀缺的、有限的。不过，物质商品与精神商品之间的替代是有限度的，人不能靠“喝西北风”生活，也不能过“行尸走肉”的生活。

事实上，在一种商品效用曲线的基础上，可以很方便地推导出，代表全部商品、体现商品之间替代与互补关系的两种商品的效用曲线或等效用曲线，即无差异曲线。序数效用论者，正是如此，在力图避免效用可以直接被计量这种尴尬假设的同时，为经济学提供了一种新的分析方法，即无差异曲线分析。

埃奇沃思首先把电磁场理论应用于经济学之中，借用其中的等势面而发明了无差异曲线。^[18]帕累托进一步地把“无差异曲线”作为一种统称，并具体命名了各种无差异曲线，比如，“无差异曲线”（indifference lines，indifference curves）、“消费者无差异曲线”（consumer’s indifference lines）、“生产者无差异曲线”（producer’s indifference lines）、“偏好无差异曲线”（indifference lines of tastes）、“预算约束无差异曲线”（indifference lines of obstacles），等等。^[19]

美国流行教材用的是“等高线”的概念［They are contours connecting points of equal height（levels of utility）on the“utility hill.”These contours are therefore curves of constant utility，also called indif ference curves.］，^[20]日本学者则直接指出“无差异曲线也就是等效用曲线”。^[21]

为了避免帕累托关于多种无差异曲线可能造成的混淆，为了与后面的等预算线、等产量曲线、等成本曲线等等保持一致，本教材将还物理学“等量面”^[22]以其原本的含义，不采用“无差异曲线”而采用“等效用曲线”的称谓。不过，此处提醒攻读研究生的同学，一定要注意这个重要的同一概念的不同用词。

关于等效用曲线的描绘，传统教材上遵循了帕累托依据“直接的经验事实”描绘序数效用下等效用曲线的方法。但是，如此则失去了心理学基础，也偏离了亚当·斯密“财富—幸福”的逻辑联结。

假设消费者个人消费代表全部商品的两种商品Q₁、Q₂的数量分别为q₁、q₂，则其效用函数U为：

上面，我们根据一种商品的效用函数式（3.3）描绘出了如图3.1所示的一种商品的效用曲线，这是基数效用下一种商品的效用曲线。以基数效用下一种商品的效用曲线为基础，约翰·希克斯（John Richard Hicks，1904—1989年），提出从理论上逻辑地推导两种商品的效用曲线的新方法等，获得1972年诺贝尔经济学奖，其方法如图3.3所示。

如图3.3，先画一根纵轴表示效用水平，再画两根横轴表示消费两种商品的数量分别为q₁和q₂，则消费商品Q₁、Q₂获得的总效用曲线分别为U_q1、U_q2。空间中的任何一点P代表消费两种商品Q₁和Q₂的一定数量的组合（PA，PB）。从P点出发，平行于纵轴，得到等效用水平的PP直线，PP直线的运动轨迹就构成了一个“效用曲面”，该效用曲面与q₁、q₂坐标相切并与U_q1、U_q2相交。

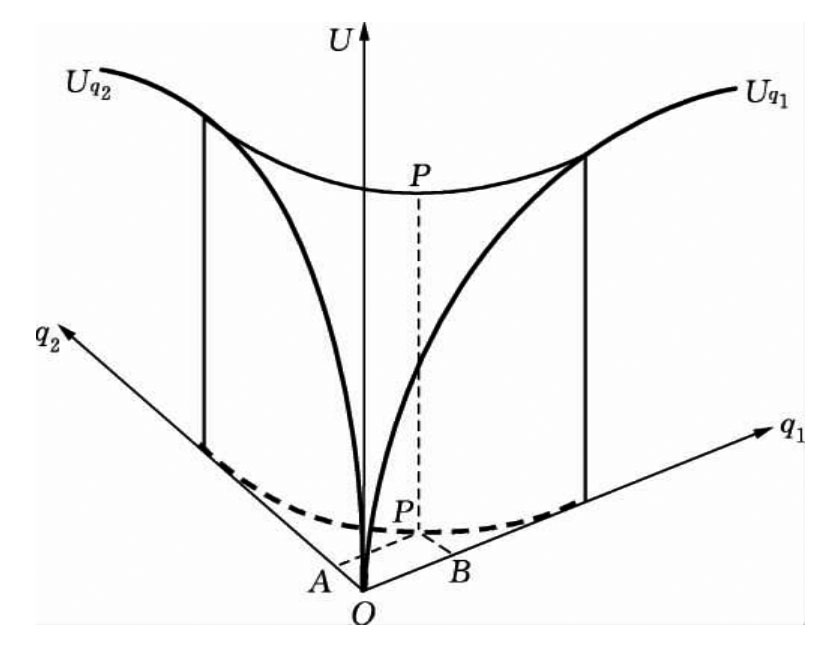
图3.3　从一种商品的效用曲线到两种商品的效用曲线

我们也可以用一个平面图代替三维图。用两根横轴表示消费两种商品Q₁、Q₂的数量q₁、q₂，就可以在q₁-q₂平面上得到PP运动轨迹所构成“效用曲面”的投影，如图3.3中的弧形虚曲线。这条曲线就是等效用曲线。它对应的第三维度上的等高线，就是把对应第三维度上所有相同高度的点连成的一条曲线，也就是把效用水平相等的点连成的一条曲线。对照图3.4，这就是说，设P和P′在同一条等效用曲线上，则表示从消费PA数量的Q₁商品和消费PB数量的Q₂商品所获得的总效用，与消费P′A′数量的Q₁商品和消费P′B′数量的Q₂商品所获得的总效用是相等的。因此，无差异曲线也称作等效用曲线。

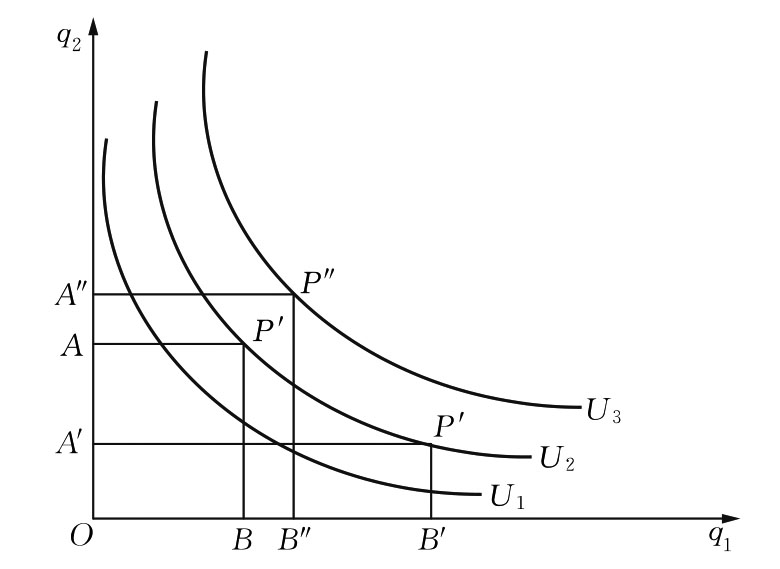
图3.4　等效用曲线

类似地，可以在q₁-q₂平面上画出许多这样的曲线，如图3.4所示。设P″在第三个维度上位于比P更高的地方，因而位于更高位置的等效用曲线上，那么消费Q₁、Q₂商品的数量组合（P″A″，P″B″）获得的总效用水平，就比消费Q₁、Q₂商品的数量组合（PA，PB）获得的总效用水平要高。^[23]

两种商品足以表达全部商品，因此，图3.4所表示的也就是全部商品的效用曲线或等效用曲线。

由此可见，等效用曲线可从一种商品的效用曲线推得。因此，无差异分析与边际分析是殊途同归的。就是说，依据希克斯的方法推导等效用曲线，就实现了基于基数效用的边际分析与基于序数效用的无差异分析的有机统一，从而说明序数效用下的无差异曲线并没有脱离人类行为的心理学基础，也因此回归到了亚当·斯密的“财富—幸福”联结的逻辑。

我们也可以把希克斯的效用三维空间几何图形（图3.3）变换成如图3.5所示的效用三维空间几何图形。

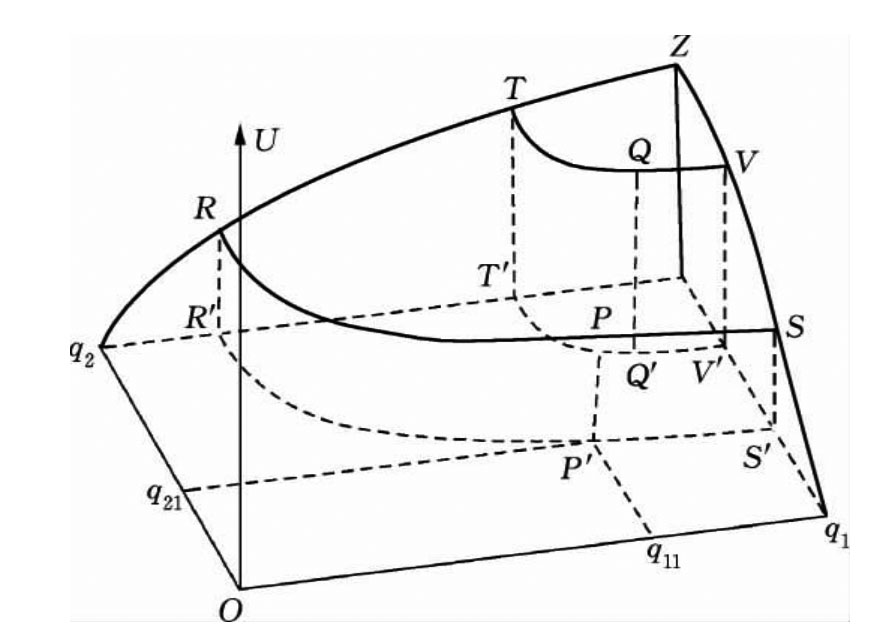
图3.5　两种商品的效用曲面和等效用曲线

图3.5中，水平面的两个坐标轴Oq₁和Oq₂分别表示商品Q₁和商品Q₂的数量，高度坐标轴表示效用水平。q₁SVZ曲线表示消费Q₂获得的总效用的曲线，q₂RTZ曲线表示消费Q₁获得的总效用的曲线。由水平面上的任何一个q₁和q₂的组合点，都可以在效用曲面Oq₁Zq₂上找到一个相应的效用水平高度。例如，在商品Q₁的数量为Oq₁₁和商品Q₂的数量为Oq₂₁的组合P′点上，相应的效用水平为PP′。如果由商品组合P′点出发，在保持效用水平不变的条件下，用商品Q₁去替代商品Q₂，或者用商品Q₂去替代商品Q₁，于是，就可以得到水平面上的曲线R′P′S′。该曲线上所有的商品组合，都可以产生相同的效用水平，即有RR′＝PP′＝SS′。可见，水平面上的R′P′S′曲线是可以给消费者个人带来一个相同效用水平的所有q₁和q₂的组合的轨迹。因此，该曲线就是一条等效用曲线。图3.5中的T′Q′V′曲线是另一条等效用曲线，它代表的效用水平高于等效用曲线R′P′S′。^[24]于是，仍然可以得出图3.4所示的等效用曲线。

等效用曲线一般具有以下特点：

（1）离原点越近的等效用曲线代表的效用水平越低，离原点越远的等效用曲线代表的效用水平越高。由于通常假定效用函数具有连续性，于是在同一坐标平面上的任何两条等效用曲线之间，存在着无数条等效用曲线。或者说，可以有无数条等效用曲线覆盖整个坐标平面。如图3.4中，离原点最近的等效用曲线U₁代表的效用水平最低，离原点最远的等效用曲线U₃代表的效用水平最高，等效用曲线U₂代表的效用水平居中。

（2）在同一坐标平面上，任意两条等效用曲线不会相交。这一点可以用图3.6说明。

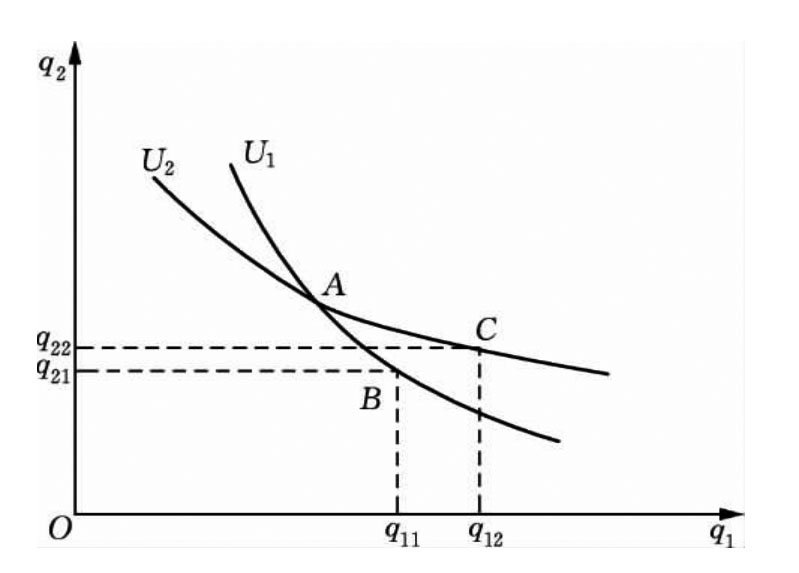
图3.6　违反偏好假定的等效用曲线

在图3.6中，两条等效用曲线U₁和U₂相交于A点。这说明等效用曲线U₁上的B点的效用水平与等效用曲线U₂上的C点的效用水平由于都等于相交点A点的效用水平而彼此相等，即消费者个人认为B点和C点是无差异的。但是，由于C点的商品组合所代表的两种商品的数量都大于对B点的商品组合，根据消费者偏好的第三个假定，消费者个人对C点的商品组合的偏好必定大于对B点的商品组合的偏好。这样一来，消费者个人在认为B点和C点无差异的同时，又认为C点优于B点，这就违反了消费者偏好的第一个假定。以此，两条等效用曲线相交是错误的。

（3）等效用曲线是凸向原点的，也称作偏好是凸型的。凸型偏好指的是关于良好品（goods）而非厌恶品（bads）。^[25]从图3.4可见，等效用曲线不仅是向右下方倾斜的，即该斜率是负值，而且等效用曲线是凸向原点的，即随着q₁的数量的连续增加，等效用曲线的斜率的绝对值是递减的。等效用曲线的这一特点是由商品的边际替代率递减规律所决定的。

2.不同性质商品的等效用曲线

为后面分析方便，此处再介绍其他一些等效用曲线。

（1）完全替代品。

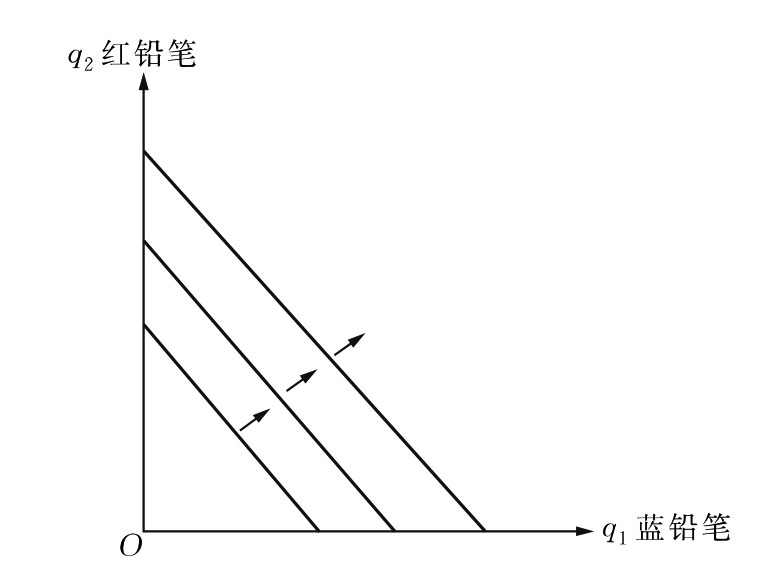
图3.7　完全替代品的等效用曲线

如果消费者个人愿意按固定的比率用一种商品代替另一种商品，那么这两种商品是完全替代品。完全替代品的最简单的例子是消费者个人愿意在1∶1的基础上替代商品。假设要在红、蓝两种铅笔之间进行选择，若消费者个人喜欢铅笔但一点儿也不在乎铅笔的颜色，那么红、蓝两种铅笔之间就是完全替代的。完全替代品等效用曲线为向右下倾斜的直线，偏好增加的方向朝着右上方，如图3.7所示：

（2）完全互补品。

完全互补品是始终以固定的比例一起消费的商品。从某种意义上说，这些商品是相互“补充”的。一个非常恰当的例子是右脚的鞋子和左脚的鞋子。消费者个人喜爱鞋子，而且总是左、右脚一起穿的。一双鞋只要少了一只，对消费者个人就毫无用处了。完全互补品的等效用曲线呈L形，偏好增加的方向朝着右上方，如图3.8所示：

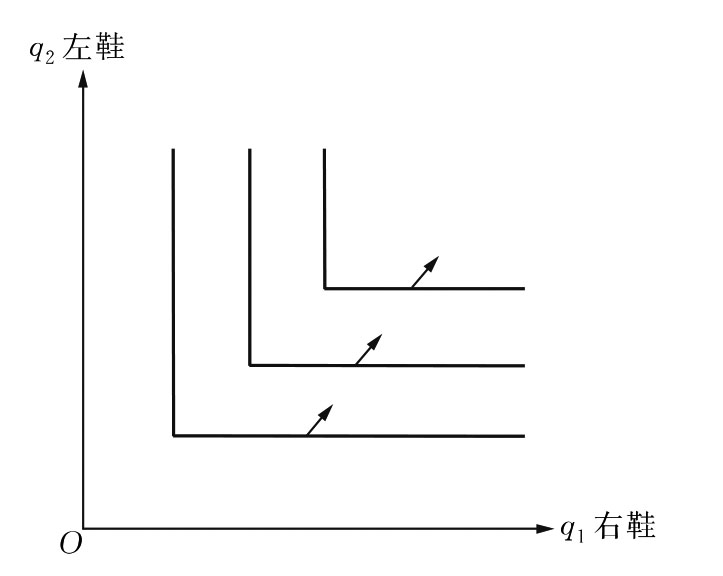
图3.8　完全互补品的等效用曲线

（3）厌恶品。

良好品（goods）是消费者个人希望多多益善的商品。假设两种商品都是良好品，则其等效用曲线凸向原点，偏好增加的方向朝着右上方，如图3.4所示。

厌恶品（bads）是消费者个人不喜欢的商品。假设有烤肠和臭豆腐两种商品，某个消费者喜欢烤肠而不喜欢臭豆腐。我们再假设在烤肠和臭豆腐之间存在着替换的可能。也就是说，当消费者个人不得不消费一定量的臭豆腐时，可以得到一些烤肠作为补偿。这样，消费者个人的等效用曲线必定是向右上方倾斜，如图3.9所示。偏好增加的方向指向右下方，即朝着臭豆腐消费减少和烤肠消费增加的方向，如图3.9中箭头所示。

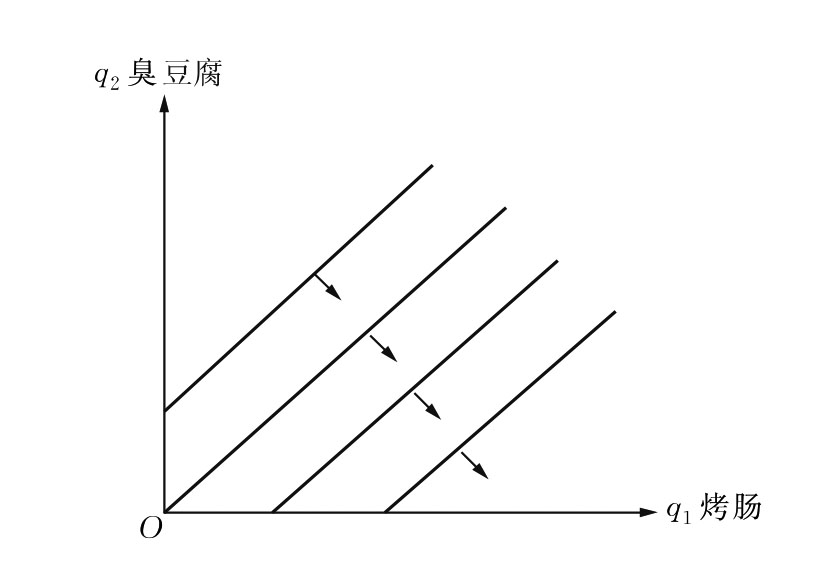
图3.9　厌恶品的等效用曲线

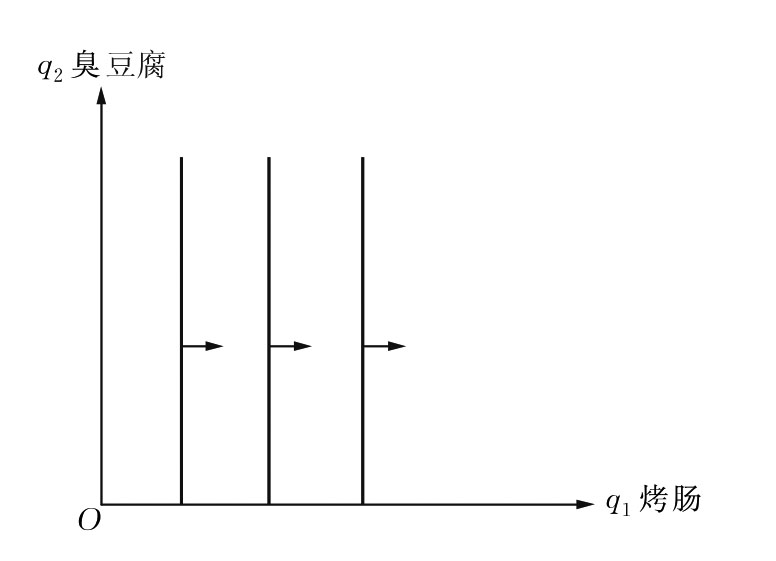
图3.10　中性商品的等效用曲线

（4）中性商品。

中性商品是消费者个人无论从哪方面说都不在乎的商品。如果某个消费者正好对臭豆腐持中立态度，在这种情况下，该消费者的等效用曲线是一条垂直线，如图3.10所示。该消费者只关心他能得到多少烤肠，而毫不关心他将得到多少臭豆腐。他得到的烤肠越多越好，但增加一些臭豆腐对他没有任何影响。

（5）餍足。

餍足（satiation）的情况，即对于消费者个人来说有一个最佳的消费组合，就他自己的偏好而言，越接近这个消费组合越好。例如，假设某消费者有某个最偏爱的消费组合（q₁₀，q₂₀），离这个消费组合越远，他的情况就越糟。此时，就可说（q₁₀，q₂₀）是一个餍足点或最佳点（bliss point），消费者个人的等效用曲线就有如图3.11所示的情形。最佳点是（q₁₀，q₂₀）。远离该最佳点的点都处于较低的等效用曲线上。

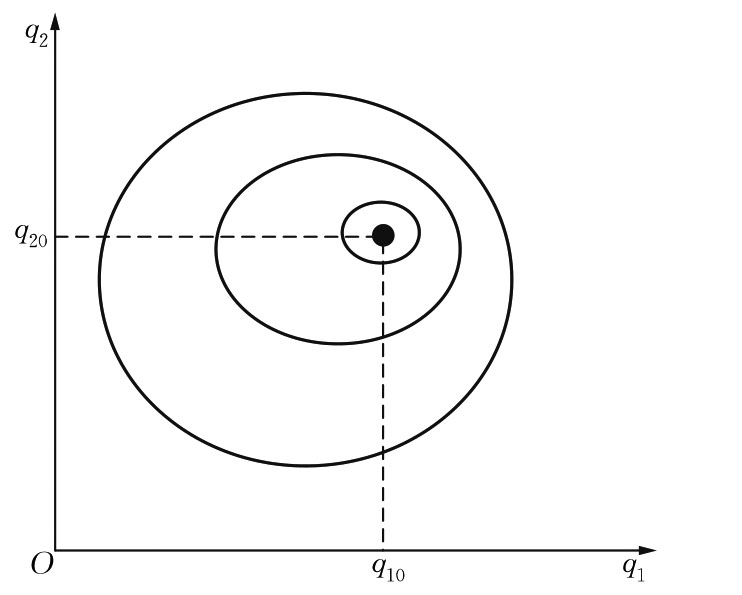
图3.11　餍足品的等效用曲线

显然，当消费者个人拥有的两种商品都太少或太多时，等效用曲线的斜率为负数；当他拥有的其中一种商品太多时，等效用曲线的斜率为正数，但这种商品就成了厌恶品，减少对厌恶品的消费会使他更接近最佳点。如果他拥有的两种商品都太多，那么这两种商品都是厌恶品，减少对这两种商品的消费使他接近最佳点。

但是，消费者个人一般不会自愿地选择过多地拥有他所消费的商品。从经济学选择的观点来看，令人感兴趣的领域是消费者个人拥有的东西往往少于他想要的。大多数商品都是这样。^[26]

四、边际替代率递减

等效用曲线是凸向坐标原点的。为了从理论上解释等效用曲线为什么具有这样的形状，希克斯在以序数效用论代替基数效用论的同时，用“边际替代率”概念取代了“边际效用”概念，又以边际替代率递减规律取代了边际效用递减规律。

1.边际替代率

边际替代率（marginal rate of substitution，简称MRS）指在保持消费者个人效用不变的条件下，一种商品能够被另一种商品替代的比率。如果把消费的商品Q₁增加Δq₁所能够替代的商品Q₂的数量Δq₂称为商品Q₁对商品Q₂的边际替代率，记为MRS_1，2，那么边际替代率用公式可表示为：

考虑其微分形式，在Δq₁→0时，有

其经济含义为：为了保持总效用不变，增加1单位商品（Q₁）可以相应减少的另一种商品（Q₂）的数量。从几何含义上看，边际替代率就是－1乘以等效用曲线上各点切线的斜率。

设商品Q₁的边际效用为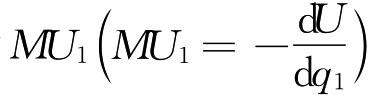，商品Q₂的边际效用为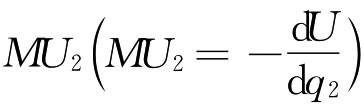），那么，当商品组合沿着等效用曲线向右下方变动时，商品Q₁消费增加Δq₁个单位，所增加的效用为（Δq₁·MU₁），同时商品Q₂的消费减少了Δq₂个单位，减少的效用为Δq₂·MU₂。由于同一条等效用曲线上效用不变，所以有：

Δq₁·MU₁＝－Δq₂·MU₂

等式（3.10）表明，边际替代率实际上等于一种商品（Q₁）的边际效用与另一种商品（Q₂）的边际效用之比。

2.边际替代率递减规律

当一种商品的消费量不断增加，在总效用不变的条件下，每单位这种商品能够替代的其他商品的数量不断减少，就是边际替代率递减规律（1aw of diminishing marginal rate of substitution）。等效用曲线凸向原点，表明其切线斜率的绝对值沿着横轴的方向递减，这一特征就是由边际替代率递减规律所决定的。

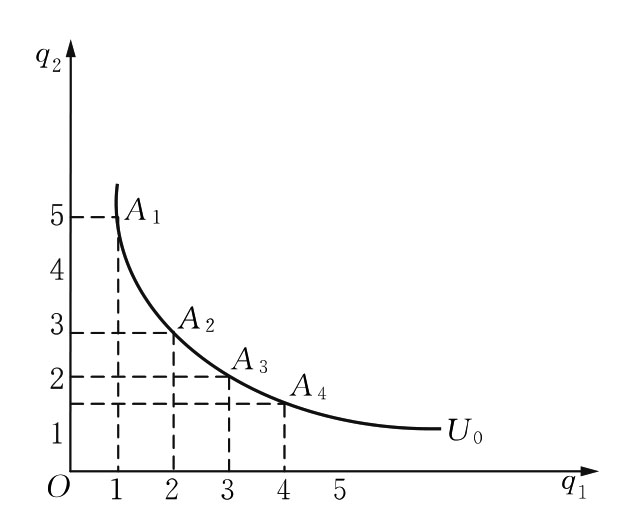
图3.12　边际替代率递减

图3.12中的等效用曲线能使我们更清楚地看出，在效用不变的条件下，增加一种商品来替代另一种商品的情况。假设效用不变（U＝U₀），从A₁（1个单位q₁和5个单位q₂的组合）开始增加q₁消费，当q₁消费增加到2个单位时，q₂消费减为3个单位（A₂点），即，增加的1个单位的Q₁商品可以替代2个单位的Q₂商品，Q₁商品对Q₂商品的边际替代率为2。当q₁继续增加到3个单位时，q₂降到2个单位（A₃点），1个单位的Q₁商品只能替代1个单位的Q₂商品，Q₁商品对Q₂商品的边际替代率降为1。如果q₁消费再进一步增加，Q₁商品的边际替代率将继续下降。这表明，为了使效用保持不变，当q₁消费不断增加时，每单位Q₁商品能够替代的Q₂商品数量不断减少，也就是说，Q₁商品的边际替代率是递减的。

3.边际效用递减规律与边际替代率递减规律

边际效用递减规律反映了，当其他商品不变时，一种商品（Q）变动与其效用变动之间的关系。边际替代率递减规律则反映了，当效用不变时，两种商品变动时的相互替代关系。虽然二者在定义上有所区别，但事实上它们又有着密切的联系。

边际效用递减规律表明，在其他商品不变的情况下，随着一种商品消费的增加，其边际效用越来越小。在这里，当Q₁商品消费不断增加时，其边际效用不断减少，Q₁商品的效用降低，从而需要更多的Q₁商品来替代Q₂商品才能保持总效用不变；当Q₂商品消费不断减少时，其边际效用不断增加，Q₂商品的效率提高，从而仅需要较少的Q₂商品来交换Q₁商品就能使总效用不变。因此，在两种商品同时变动而效用不变的情况下，边际效用递减规律就表现为边际替代率递减规律。

从式（3.10）中可以看出，由于边际效用递减规律的作用，随着Q₁商品消费的增加，分子MU₁在递减，而Q₂商品消费的减少使分母MU₂递增，所以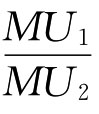的值随着商品Q₁的增加而减少，等效用曲线斜率的绝对值也随着商品Q₁的增加而减少。也就是说，等效用曲线越来越平坦，表现为等效用曲线凸向原点。