消费者个人的预算约束

第二节　消费者个人的预算约束

上面讲过，消费者个人的满足要通过消费商品才能获得，而要消费商品就必须首先用现有的财富收入去购买商品，即便贷款也是如此。就是说，消费者个人的幸福或满足最大化，在分析了商品的效用之后，要受到消费者个人现有财富收入预算的约束。

一、预算线

预算线又称为预算约束线，表示在消费者个人收入和商品价格既定的条件下，消费者个人的全部收入所能购买到的两种商品的不同数量的组合。

假定某个消费者个人有一笔收入为80元，全部用来购买商品Q₁和商品Q₂，商品Q₁的价格为4元，商品Q₂的价格为2元。那么，全部收入都用来购买商品Q₁可得20单位，全部收入都用来购买商品Q₂可得40单位。由此做出的预算线为图3.13中的AB线段。

在图3.13中，预算线AB把平面坐标图划分为三个区域：预算线AB以外的区域中的任何一点，如C点，是消费者个人利用全部收入不可能实现的商品购买的组合点。预算线AB以内的区域中的任何一点，如D点，表示消费者个人的全部收入在购买该点的商品组合以后还有剩余。唯有预算线AB上的任何一点，才是消费者个人的全部收入刚好花完所能购买到的商品组合点。

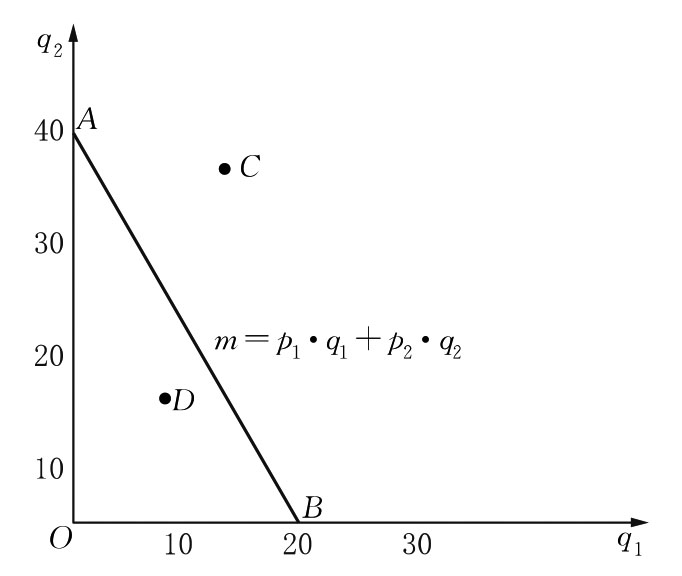
图3.13　预算线

如果以m表示消费者个人的既定收入，以p₁和p₂分别表示已知的商品Q₁和商品Q₂的价格，以q₁和q₂分别表示消费商品Q₁和商品Q₂的数量，那么预算线的方程为：

式（3.11）表示：消费者个人的全部收入m等于他购买商品Q₁的支出与购买商品Q₂的支出的总和。

由式（3.11）可得，消费者个人的全部收入购买商品Q₁的数量为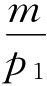，它是预算线在横轴的截距，即为图3.13中OB。消费者个人的全部收入购买商品Q₂的数量为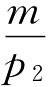，它是预算线在纵轴的截距，即为图3.13中OA。预算线的斜率为：

这说明预算线的斜率可以表示为两商品价格之比的负值。当然，式（3.11）的预算线方程也可改写为：

很清楚，式（3.13）中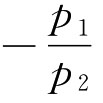为预算线的斜率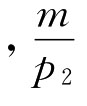为预算线在纵轴的截距。

二、预算线的变动

既然预算线表示，在一定的收入m的限制下，当两种商品的价格为p₁和p₂时，消费者个人可以购买到的两种商品的各种组合。所以，消费者个人的收入m或商品价格p₁、p₂发生变化时，便会引起预算线的变动。这一变动可以归纳为以下四种情况：

第一种情况：当两种商品的价格不变，消费者个人的收入发生变化时，预算线的位置会发生平移。这是因为，商品的价格不变，则预算线的斜率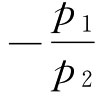不变。于是，收入的变化只能引起预算线的截距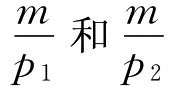的变化。如图3.14（a）所示：假定原有的预算线为AB，若消费者个人的收入增加，则使预算线由AB向右平移至A′B′。它表示消费者个人的全部收入用来购买其中任何一种商品的数量都因收入的增加而增加了。若消费者个人的收入减少，则使预算线由AB向左平移至A″B″。它表示消费者个人的全部收入用来购买其中任何一种商品的数量都因收入的减少而减少了。

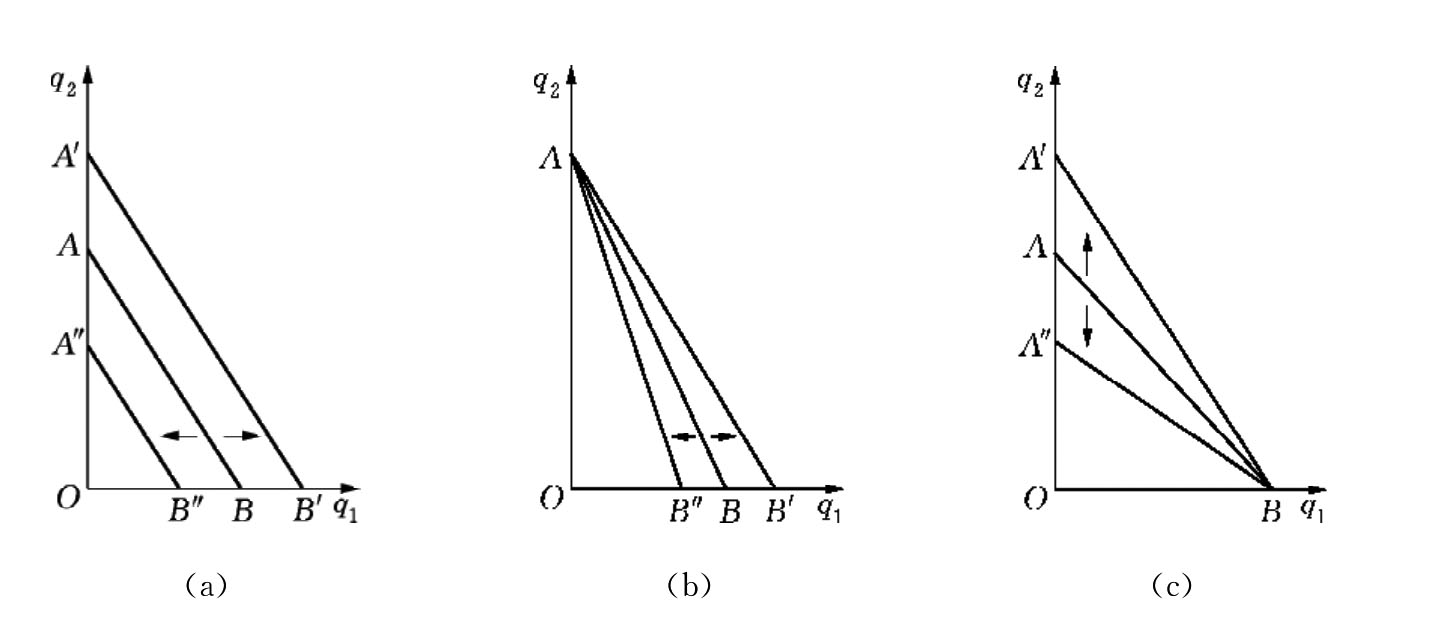
图3.14　预算线的变动

第二种情况：当消费者个人的收入不变，两种商品的价格同比例同方向变化时，预算线的位置也会发生平移。这是因为，两种商品价格同比例同方向的变化并不影响预算线的斜率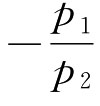，而只能引起预算线的截距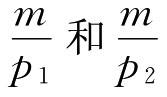的变化。仍以3.14（a）说明：若两种商品的价格同比例下降，则预算线AB向右平移至A′B′；若两种商品的价格同比例上升，则预算线向左平移至A″B″。前者表示消费者个人的全部收入用来购买其中任何一种商品的数量都同比例于价格的下降而增加，后者则表示都同比例于价格上升而减少。

第三种情况：当消费者个人的收入不变，一种商品的价格不变而另一种商品的价格发生变化时，不仅预算线的斜率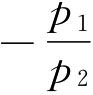会发生变化，而且预算线的截距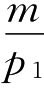或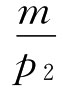也会发生变化。以图3.14（b）来说明：假定原来的预算线为AB，若商品Q₁的价格p₁下降，则预算线由AB移至AB′，它表示消费者个人的全部收入用来购买商品Q₁的数量因p₁的下降而增加了，但全部收入用来购买商品Q₂的数量并未受到影响。同理，若商品Q₁的价格p₁提高，则预算线由AB移至AB″。

类似地，在图3.14（c）中，商品Q₂的价格的下降与提高，分别使得预算线由AB移至A′B和A″B。

第四种情况：当消费者个人的收入和两种商品的价格都同比例同方向变化时，预算线不发生变化。这是因为，此时预算线的斜率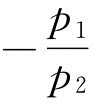不会发生变化，预算线的截距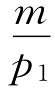和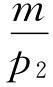也不会发生变化。这说明消费者个人的全部收入用来购买其中任何一种商品的数量都是不变的。