风险与资产选择

第五节　风险与资产选择

我们前面所讲内容都有一个共同前提：经济行为都是在确定性条件下进行的。实际上，不确定性是经济活动中的常态，而确定性是人们追求的、便于分析的偶然状态。任一经济活动所受到的影响都是复杂多样的。在通常情况下，为了简化分析，影响较小的因素忽略不计，只分析其中较为重要的方面。这样，就近似看作确定性经济行为了。

经济行为的最终结果都要进行价值评价分析，而资本货币是其核心的工具与内容。因此，资本货币问题与不确定性问题紧密相连，其中的风险分析是其理论核心。资本与风险如影相随。经济中的每一个人对风险的态度不相同，每一个人的经济行为策略也就不同。简言之，追求偏好或效用最大化的资本要素所有者，由于风险的存在与不同资本要素所有者的风险偏好差异，每个资本要素所有者投资决策的资产选择也不一样。

一、风险与风险偏好

1.风险与风险偏好的定义

风险（risk）是指厂商或个人，在经济活动中，面对不确定性的经济环境发生损失的变动性或可能性。因此，人们如何通过自身的理性认知判断风险、规避风险、利用机会获得收益等等，就成为应对不确定性的经济环境采取不同的策略措施所应考虑的问题。

每个人对风险的态度是不一样的。一个人在面对风险时采取经济行为的态度就叫风险态度或风险偏好（risk preference）。例如，对赌博活动的态度：赌博可能给人带来较高收益，同时也可能给人造成损失。但在面对同样的赌博活动时，不同的人可能会采取不同的行为。“抛硬币”是最常见的赌博行为。这种赌博行为的风险在于：硬币抛下若为正面自己可赢例如500元，但硬币抛下若为反面自己就失去500元。这种赌博的期望值最终为0（即赢500元和失去500元的概率都为50%或0.5）。我们通常称期望值为0的赌博为公平赌博。

为分析需要，我们将人们的风险偏好划分为三类：风险爱好型、风险中性型和风险厌恶型。风险爱好型的人或风险爱好者（risk lover），指那些在一定的确定性收入或消费与具有相同期望价值的风险收入之间进行比较选择而更偏好于后者的人。例如，在上面的“抛硬币”赌博中，不参加赌博的确定性收入或消费为0，参加赌博的期望收益也为0，但风险爱好者就会更倾向于选择后者而参加这种赌博。风险中性型的人或风险中性者（risk neutral）是指那些认为一定的确定性收入或消费与具有相同期望价值的风险收入之间没有差异的人。如那些对参加不参加上面的“抛硬币”赌博无所谓的人。风险厌恶型的人或风险规避者（risk evader）是指那些在一定的确定性收入或消费与具有相同期望价值的风险收入之间进行比较选择而更偏好于前者的人，如那些从不参加上面的“抛硬币”赌博或类似活动的人。

不同的风险偏好会造成不同的人面对相同或相似经济环境的经济决策不同，从而使经济活动千变万化。这是经济不确定性的重要体现，也是信息经济学理论研究与应用的重要领域。

2.期望效用函数

我们将人们面对风险的态度划分为三类，但现实中的人的风险态度要复杂得多。我们这里只是简要进行原理性分析。

由于实际的偏好多种多样，那么，利用什么区分这些偏好的差异呢？我们通常利用期望效用（expected utility，简称EU）的大小来区分每一个人的风险偏好情况，并利用期望效用函数（expected utility function）来分析人们面对风险时的决策情况。期望效用理论（expected utility theory）是冯·诺伊曼和摩根斯坦在20世纪40年代出版的《博弈论与经济行为》（1944）一书中提出的。著名数学家冯·诺依曼（John von Neumann）和著名经济学家奥斯卡·摩根斯坦（Oskar Morgenstern）从一系列公理化理性偏好出发，建立了不确定条件下对理性人（rational actor）选择进行分析的框架。他们认为，在理性人面对不确定情况下的选择问题时，总是选择给自己带来最高期望效用而不是期望值的一方。期望效用（expected utility）是指在各种情况下根据对应发生概率所获取的收入或消费而计算的效用，期望效用函数（expected utility function）就是根据一些假定而计算或表达收入或消费的效用大小变化的函数。

假定消费者在1、2两种情况或状态下，获得的收入或消费分别为c₁、c₂，它们对应发生的概率分别为p、1－p；一般效用函数为U（c_i），即消费者对确定性收入c_i的效用函数。那么，该消费者的期望效用函数为：

式（11.8）就是期望效用函数，也称冯·诺依曼—摩根斯坦效用函数（von Neumann-Morgenstern utility function）。等式左边的EU就是期望效用，等式右边的p U（c₁）＋（1－p）U（c₂）就是期望收入或消费（expected value），即消费者收入或消费的期望值。显然，期望效用EU实际上就等于一般效用函数为U（c_i）在各个概率水平上的加权平均值。

当然，可以将上述情况一般化，即若有n种情况，每种情况发生的概率为p_i（i＝1，2，…，n），那么，消费者的期望效用函数为：

这也就是冯·诺伊曼—摩根斯坦效用函数的一般表达形式。

由此，我们就可以比较简便地表达和分析人们的风险偏好了。我们在这里进行一般化分析，见图11.9：

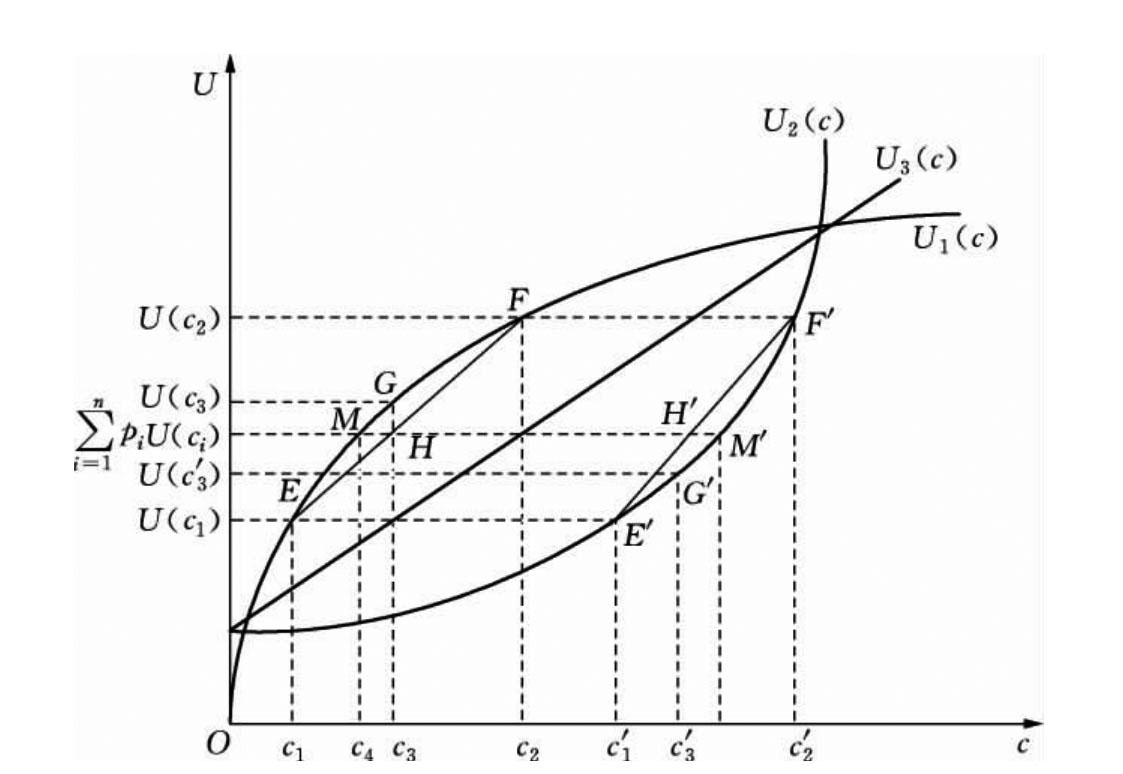
图11.9　风险偏好的区分

假定某消费者有财富收入m（＝c₃），并与某对手赌博，赌赢的概率为p＝50%而得到对手相当于c₁的财富，赌输的概率就为（1－p）＝50%而付给对手相当于c₁的财富，消费者收入将由固定不变的确定性财富收入m变为不确定性收入（c₂，c₁；50%）：50%的机会获得c₁，50%的机会最后只持有c₂（＝c₃－c₁），或失去一个c₁。

消费者的期望收入为：c₃＝50%×c₂＋50%×c₁

这一赌博可被看作是公平的，因为参赌双方面对的情况都是一样的，没有哪一方占有优势。消费者对收入或消费（c₂，c₁；50%）的期望效用为：

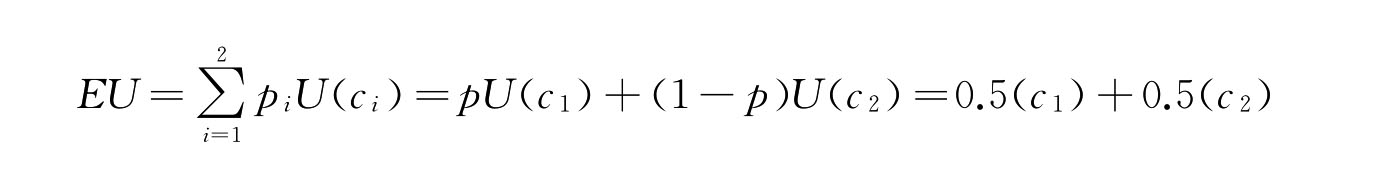
（1）在图11.9中，横坐标轴c表示收入或消费，纵坐标轴U表示消费者对确定性收入或消费的效用。消费者1具有图中确定性收入效用函数曲线的U₁（c），我们标出了确定性收入或消费c₁、c₂和c₃的效用值U（c₁）、U（c₂）和U（c₃），还有不确定收入或消费（c₂，c₁；50%）的期望效用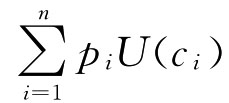（在图中分别对应E点、F点、G点和H点）。可以看到，

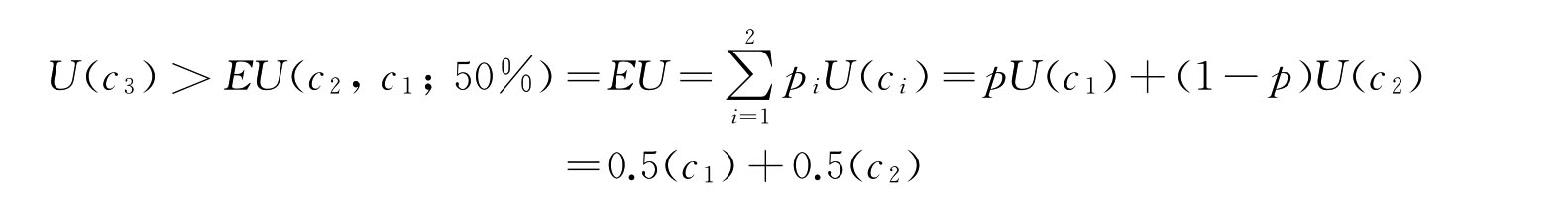
也就是说，G点的效用值大于H点的效用值，该消费者在面对确定性收入c₃和不确定性收入（c₂，c₁；50%）时，他更偏好选择确定性收入c₃，他厌恶参加这个公平性的赌博。这样，由于该消费者在面对不确定性收入或消费和期望值相等的确定性收入或消费时，更偏好于确定性收入或消费，即认为前者的效用小于后者的效用（在图中分别对应H点与G点），我们就说这个消费者1是风险厌恶型的或风险规避型的。在图中，该消费者认为不确定性收入或消费（c₂，c₁；50%）与确定性收入或消费c₄的效用是无差异的（在图中分别对应H点与M点）。也就是说，在面对不确定性收入或消费（c₂，c₁；50%）时，该消费者愿意放弃（c₃－c₄）的期望收入或消费，以换取确定性收入或消费c₄。我们就可以将c₃和c₄的缺口称为风险溢价、风险升水或风险贴水（risk premium），这表示风险厌恶者为规避风险而愿意付出的代价。显然，风险贴水越高，该消费者的风险厌恶程度越高。

（2）在图11.9中，同（1）的分析类似。另一消费者2有确定性收入效用函数曲线的U₂（c），我们同样可标出确定性收入或消费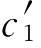、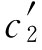和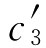的效用值U（c₁）、U（c₂）和U（c₃），还有不确定收入或消费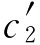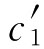，；50%）的期望效用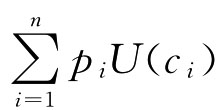（在图中分别对应E′点、F′点、G′点和H′点）。但是，我们却看到消费者2认为：

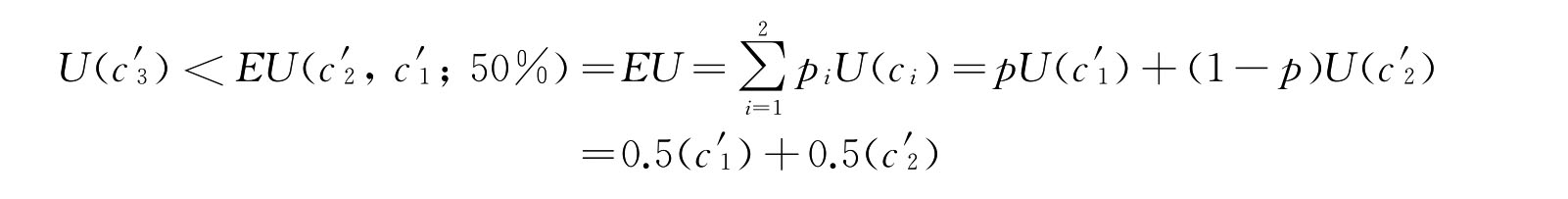
也就是，H′点的效用值大于G′点的效用值，该消费者在面对确定性收入c′₃和不确定性收入（c′₂，c′₁；50%）时，他更偏好选择不确定性收入（c′₂，c′₁；50%），他更偏好参加这个公平性的赌博。我们就说这个消费者2是风险偏好型的或风险爱好型的。

（3）在图11.9中，与（1）、（2）同样的分析。还有消费者3有确定性收入效用函数曲线的U₃（c）。通过分析，我们发现，该消费者对不确定性收入或消费与价值等于其期望值的确定性收入或消费具有相同的偏好，或者谈不上厌恶或喜好这类公平的赌博。我们就称该类消费者为风险中性型的，他介于风险厌恶型与风险偏好型之间。

这样，我们就可看到，风险厌恶型的消费者的效用函数曲线是下凹的曲线，风险偏好型的消费者的效用函数曲线是上凹的曲线，风险中性型的消费者的效用函数曲线是一条直线。所以，个人对风险的态度与边际效用密切相关，边际效用递减规律就对个人风险态度有内在影响，换句话说，人们对自己所拥有财富的效用看法就影响其风险态度。

在实际经济活动中，前已述及，人们的风险态度是复杂的。不单人们风险厌恶或偏好的程度不同，而且一个人的风险态度还可能不是一成不变的，有时表现为风险厌恶型的，有时又呈现出风险偏好型的，有时又无所谓。但是，从总体而言，不论是人类总体，还是一个人总的经济活动来看，由于边际效用递减规律终究会发挥作用，人们的风险态度较多时候还是表现为风险厌恶型的。

二、风险规避

正是由于人们在通常情况下都表现为风险厌恶型的，一般而言，人们在进行经济活动中都想尽办法尽量降低风险或规避风险，比如转移风险、分散风险等。

通过转移风险的方式降低风险也可以分为多种方式。比如套头交易或掉期交易（hedge or swap transaction）、分包（subcontract）、保险（insurance）。

1.套头交易与掉期交易

套头交易也叫对冲交易（hedge），是指通过不同期货的买卖（如粮食期货等商品期货、外汇期货等金融期货），将未来各种风险转移给他人，以减少可能的损失。

例如，有一家大型养猪场为减少饲料价格波动带来的损失，他可以通过玉米或大豆的套头交易获得稳定的饲料价格，从而稳定生猪饲养成本核算。具体可操作为：如6月1日购进1万吨玉米，每吨2 000元；同时他从经纪人处购进1万吨玉米期货，价格为每吨2 200元，期货规定12月底交货。到10月1日，玉米价格上升，他又购进1万吨玉米，每吨2 500元；同时他又通过经纪人卖出1万吨玉米期货，价格为每吨2 700元，交货日期也是12月底。这样，虽然10月1日玉米价格上升了，在现货交易中，养猪场每吨成本增加500元，但从期货交易中，每吨却赚了500元。两者相抵，玉米饲料成本并没有因其价格波动而提高，这样，该大型养猪场就把饲料价格波动风险转移给了他人。

掉期交易（swap transaction）是通过即期买卖和远期买卖相结合的一种交易方式，即在买进或卖出即期货币的同时，卖出或买进数额相通的远期货币，从而达到规避风险、实现保值的目的。掉期交易可分为三类：（1）即期对远期交易（spots-forward swaps），即一笔为即期交易，另一笔为远期交易；（2）隔日掉期交易（tomorrow-next swaps），即一笔交易是在成交后第一个营业日交割，另一笔交易则于成交后第二个营业日交割的掉期交易；（3）远期对远期的掉期交易（forward-forward swaps），即两笔交易均在两个营业日以上交割的掉期交易，且期间都不相同。

不论是对冲交易还是掉期交易，都是通过套期操作获得保值功能，以期转移损失风险，降低经济风险。当然，这些交易也可以用于投机（speculation），就是不管交易的对象是什么，不进行套期对冲，凭借自身判断只要赚取更大利润就行，显然，他们判断错误要承担较大损失，这就是投机者的行为。实际上，投机者承担了保值者（如风险厌恶者）的部分风险，他们的行为就接近于风险偏好者的经济行为。

2.分包

分包（subcontract）有时也可叫转包，它是指投资人在从事经济活动中将经营活动的一部分通过一定协议分给他人的方式，借以尽量规避风险，降低损失可能性。如一家建筑公司或一家安装公司在承接总投资20亿元的某工程后，为了降低经营风险或保障赢利（可能由于资金紧张、技术短缺、价格波动、规模实力等方面的原因），它可能将其中某些小工程再次经过招标等方式进行分包或转包他人，最终完成该大型工程建设。在这一过程中，该建筑公司或安装公司通过分包合同将亏损的风险转移给了他人，从而降低了自身风险。

3.保险

保险是现代经济社会中最常见的规避风险的方式。总的来讲，保险人通过签订保险合同、交纳一定保险费用将风险转移给了保险公司，从而降低了自身损失的风险。

我们可以从公平精算保险（actuarially fair insurance）分析开始。“公平”保费就是对保险公司和被保险人来说期望收益都是0，就是保险费等于保险提供人的期望支出。

假设某人现有财产为A，有概率为p的可能性损失B。假设保险市场的保险费率为λ，如果他投保金额为J，则需支付的保险费用为λJ。假设不存在运营费用，则保险公司从投保人得到的期望利润为：

假如保险市场是完全竞争市场，这样Eπ＝0，即λ＝p，保险费率等于损失发生的概率，这被称为公平的保险费率。

那么，如果保险费率是公平的，即λ＝p，有多少财产投保呢？投保人的目标是期望效用最大化，即：

求其极值，可得：

等式左边是损失发生时的边际效用，等式右边是损失没有发生时的边际效用。这就表明，投保人的最优选择是使得损失发生时1元钱的额外收入的边际效用等于不发生损失时1元钱额外收入的边际效用。

从式（11.11）可知，投保人的期望财富效用值EU为：

因此，对于风险厌恶型的投保人而言，不论损失是否会发生，投保人都可确定地得到（A－p B），而与投保金额J大小无关。

从式（11.12）可知，为满足等边际效用的原则，要求（A－B＋J－λJ）＝A－p J，即J＝B。也就是说，在公平的保险费率下，风险厌恶者会选择全额保险。

保险从表面上看是保险公司向保险人提供了损失补偿，替被保险人承担了风险，但实际上，并不是保险公司真正提供了保险或赔偿了损失。例如，在交通事故保险中，发生事故的风险通过许许多多面临该类风险的投保人的分担而分散了，也就是说，实际发生事故的人的损失是由那些没有遭受损失的投保人支付了赔偿，保险公司只是因为经营或中介了这种风险损失支付而获利。

正是这种风险转移分担特性，使得保险市场才能有效运作。但是，必须满足两个前提条件：一是分担风险的人必须是相互独立的，否则就无法分担风险，例如地方性的保险公司是没有办法独立承担诸如洪水、地震等自然灾害业务。也正是为了充分保证风险的独立性，再保险（reinsurance）业务也逐渐发展起来，以进一步在更广范围内进行风险转移或分担。二是不应当存在或避免严重的道德风险（moral hazard）和逆向选择（adverse selection）行为。这两个问题在信息经济学中或本教材第二十五章的市场失灵中进行介绍。

三、资产组合选择

在现代社会经济中，一个人所拥有财富的存在形式可以是多种多样的，如现金货币、外币、股票、债券、各种存款、技术专利、房产、土地、矿山、粮食、货物等等各种资产形式。由于经济环境的变化和人们社会习俗偏好的变化，各种资产的价值都可能发生波动。“不要把所有鸡蛋放到一个篮子里”，这已经成为人们关注资产组合的常识性共识之一。但是，到底应当以何种形式保存财富才能保证资产价值不贬值甚至升值呢？这就是资产组合选择问题应当研究的内容。基于资产的流动性和有效保值增值方式来看，在现代经济中，最受关注的就是证券投资过程中的资产组合选择问题。

现代资产组合理论是由美国纽约市立大学巴鲁克学院的经济学教授哈里·马科维茨（Harry M.Markowitz，1927—　）于1952年建立的。他与威廉·夏普（William Sharpe，1934—　）和默顿·米勒（Merton Miller，1923—2000年）一起，由于提出了有关预期收益和风险之间相互关系的资产组合选择理论，为现代证券投资理论的建立和发展奠定了基础，而分享了1990年度诺贝尔经济学奖。而资本资产定价模型（capital asset pricing model，简称CAPM）是首先由夏普在1963年发表《证券组合分析的简化模型》一文中提出的，是继马科维茨的现代资产组合理论之后，由威廉·夏普、约翰·林特尔（John Linter）、杰克·特里诺（Jack Treynor）和简·莫森（Jan Mossin）等人共同创立的、最著名的证券投资模型，它已成为现代金融市场定价理论的支柱，被广泛应用于投资决策和公司理财等领域。

1.如何进行资产组合选择

不同的资产会给所有者带来不同的收益，同样，证券市场的瞬息万变使得不同的证券会给证券拥有者带来瞬息万变的收益或损失。

现代资产组合理论（modern portfolio theory，简称MPT），也有人将其称为现代证券投资组合理论、证券组合理论或投资分散理论。其主要结论是：只要不同资产之间的收益变化不完全正相关，就可以通过资产组合方式变化来降低投资风险。该理论将风险分为两种：系统风险（systematic risk）和非系统风险（unsystematic risk）或特殊风险（unique risk or idiosyncratic risk）。前者指由整个经济环境产生的风险无法由投资组合来降低；后者是指个别企业或个人面对的风险，对单个企业或个人而言投资是不确定性的，这可以通过资产组合降低风险。

1952年3月马科维茨在《金融杂志》上发表《资产组合的选择》一文，利用概率论和线性代数分析证券投资组合问题，并于1959年出版《证券组合选择》一书，详细论述了证券组合的基本原理，从而形成较为完整的现代投资组合理论。该理论主要针对如何化解投资风险提出的。

马科维茨在1952年提出了“均值－方差组合模型”。它假定没有融券和没有无风险借贷前提下，利用多种个别证券收益率均值μ和方差σ₂寻找出投资组合的有效边界（efficient frontier），即在一定收益率水平下方差σ₂最小的投资组合。这样，所有挑选的股票间的相关系数都是较低的，也就是说，这一模型不只要求投资不同证券，还应投资不同产业的证券。该模型利用均值－方差效用函数分析人们的风险态度，建立模型分析基础。

均值－方差效用函数为：

若由于非系统风险的存在，投资者未来的财富或收入就可能成为一个随机变量，如以p_i的概率分别表示为w_i，i＝1，2，…，n，那么，均值μ和方差σ₂就可有如下公式计算而得：

而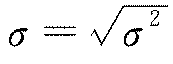就称作投资收益的标准差。

均值μ体现了投资的未来“平均”收益的大小，方差σ²（或标准差σ）体现了未来收益的离散程度即收益额的变化范围。显然，在未来投资平均收益均值μ既定条件下，风险厌恶者总是希望方差σ²（或标准差σ）越小越好，而风险偏好者总是希望方差σ²（或标准差σ）越大越好。由于通常情况下我们都认为人们是风险厌恶者，因此，风险厌恶者财富效用函数曲线是下凹的，方差σ²（或标准差σ）的增大会降低未来的效用水平，即式（11.13）随σ²（或标准差σ）增加而降低。

那么，具体如何进行资产投资组合呢？马科维茨在《资产组合的选择》一文开始就说：“选择资产组合的过程可以分成两个阶段。第一阶段通过观察与经验，最后获得相关证券未来业绩的预测。第二阶段通过相关的预测最终选择合理的资产组合。”我们简要说明如下：

假定在投资市场中只有两种资产选择：风险资产（risky asset）和无风险资产（risk-free asset）。风险资产以p_i的概率获得r_i的资产收益率，r_m为风险资产期望收益率的均值，σ_m为对应的标准差。投资者从无风险资产获得固定投资收益率r_f。假定这个投资者将财富的x比例分配于风险资产，（1－x）比例分配于无风险资产。那么这一资产组合的期望收益均值E（r_i）为：

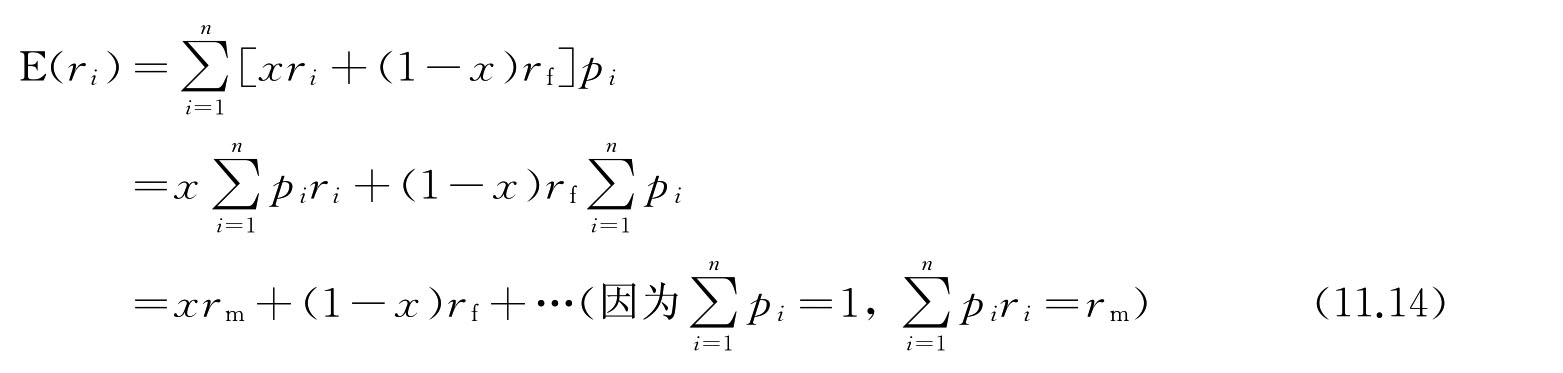
其中，i＝1，2，n＝2。

其资产组合收益方差为：

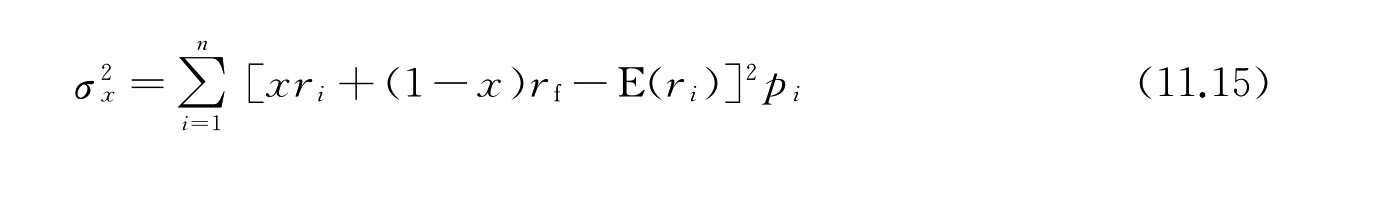
由式（11.14），整理式（11.15）为：

简化为：

我们可以分别以资产组合选择的均值和标准差为纵横坐标画图表现组合选择，参见图11.10：

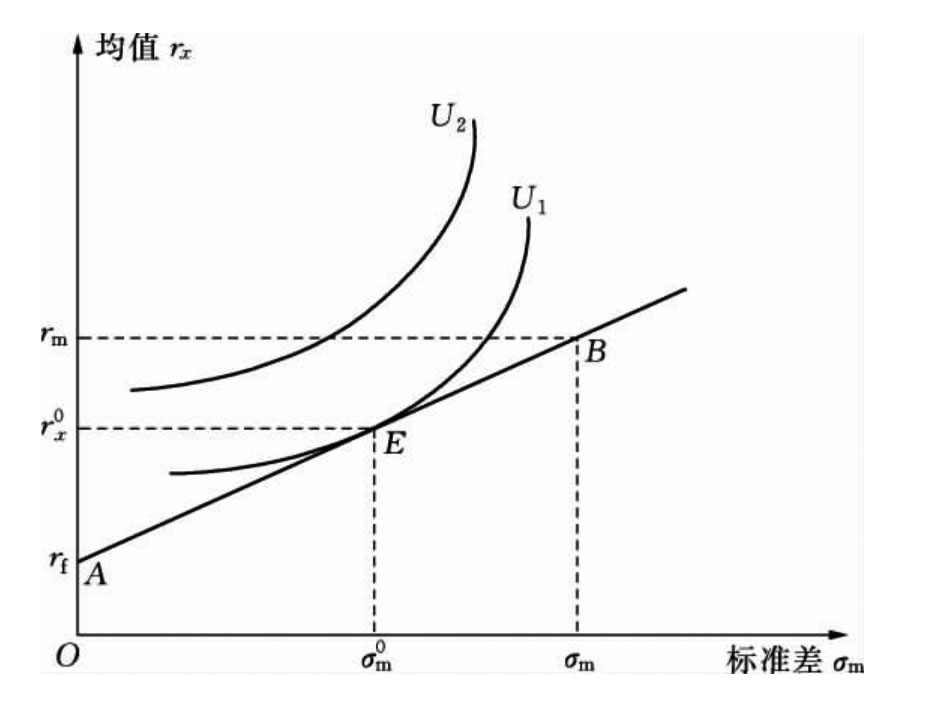
图11.10　资产组合选择

图11.10中U₁、U₂是根据均值—方差效用函数特性画出的效用等效用曲线，r_x＝E（r_i），A、B两点分别代表投资者所有财富投入到无风险资产或风险资产时的均值—标准差，A点为（r_f，0），B点为（r_m，σ_m）。若财富在两类资产中组合分配比例x在0与1之间，那么，对应的均值—标准差组合点就是AB上的其他点。也就是说，AB直线方程为：

AB直线就是投资者关于风险资产投资期望收益的预算约束线。这样，我们就可以根据等效用曲线和预算约束线寻找最优的资产组合，即图中的E点，最优资产组合就应选择E点的资产组合。而（r_m－r_f）称作风险贴水，AB直线的斜率（或两条曲线在E点相切切线斜率）称为风险价格p，它表明两类资产组合的比例变化：

也就是，风险价格p等于风险资产期望收益率与无风险资产收益率的差额（或风险贴水）除以风险资产收益率的标准差。正是由于风险资产有不同价格p，我们可以从式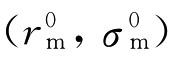（11.18）知道市场中风险资产的吸引力与其期望收益率成正向关系，而与其标准差成反向关系。风险资产定价是理论与现实中的复杂问题，下面主要介绍其中最著名的资本资产定价模型。

2.资本资产定价模型

资本资产定价模型（CAPM）是建立在马科维茨模型基础之上的，主要由马柯维茨教授的学生、美国斯坦福大学教授威廉·夏普建立的，它实际上是资本市场均衡模型。

马科维茨的模型的假设除了上述已经提及的诸如投资者是风险厌恶型的、投资不在同一行业的证券等等外，它还要求有证券市场是有效而无摩擦的：信息是充分的，投资者清楚了解市场上各类证券风险与收益率的影响因素；投资者可用具有不同概率分布的收益率评估投资结果；分析的时间期限有限；投资品市场具有充分的供给弹性，即摒除了市场供求因素对证券价格和收益率的影响；等等。尽管这些假定太严格，远离现实，但马科维茨模型为我们进行资产组合选择提供了基本分析主线。

资本资产定价模型不仅关注到非系统风险对风险资产期望收益的影响，也关注各类风险资产之间相互关系变化的影响，以及系统风险（整个经济环境、市场的风险）对各证券等风险资产期望收益的影响。为此，在选择多种风险资产进行投资时，我们引入一个衡量某一风险资产相对风险程度的系数β，β_i就表示第i种证券相对于整个证券市场的风险度，即：

式中β_i为证券i的相对风险度，cov（r_i，r_m）是证券i的期望收益与整个市场证券组合期望收益的协方差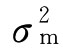是整个市场证券组合的方差。

因此，β是用来衡量一种证券或一个投资组合相对总体市场的波动性（volatility）的风险评估工具。例如，若第i类股票的价格和市场的价格波动性一致，则该股票的β_i＝1。若某个股票的β＝2，意味着当股市指数上升1%时，该股票价格则上升2%；而市场下降1%时，股票的价格亦会下降2%。1972年，经济学家费希尔·布莱克（Fischer Black）、迈伦·斯科尔斯（Myron S.Scholes）等发表《资本资产定价模型：实例研究》一文，研究了1931—1965年纽约证券交易所股票价格的变动，证实了股票投资组合的收益率和它们的β值之间存在着线形关系。

如果投资者对各类风险资产进行投资，通过市场信息交流和交易过程，最后投资者要达到资本市场投资均衡，必定要实现在通过风险程度调整后各类风险资产收益率相等。

怎样调整各类风险资产的风险值呢？通过上述分析，我们可知，第i类风险资产的风险总量可计算为β_iσ_m，因此，它的风险调整值就等于风险价格p与其风险总量的积，即：

第i类风险资产的风险调整值＝β_iσ_mP＝β_iσ_m·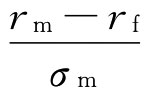＝β_i（r_m－r_f）

若只有风险资产i和无风险资产f两类可供投资者进行投资，那么，风险资产i的期望收益率r_i经过风险调整后应等于无风险资产期望收益r_f：

r_f＝r_i－β_i（r_m－r_f）

即：

式（11.19）就是资本资产定价模型公式。

根据前述，式（11.19）说明了：任一种风险资产的均衡收益率r_i（风险资产期望收益率的均值）可分为两部分：一是r_f，即投资者从无风险资产获得固定投资收益率，实际就是前述内容中资本供求市场的均衡利率；二是β_i（r_m－r_f），即根据风险资产风险大小进行的风险调整值，我们称之为“风险溢价”（risk premium）或风险收益率。由此，我们可以得到风险资产的市场线（market line），参见图11.11：

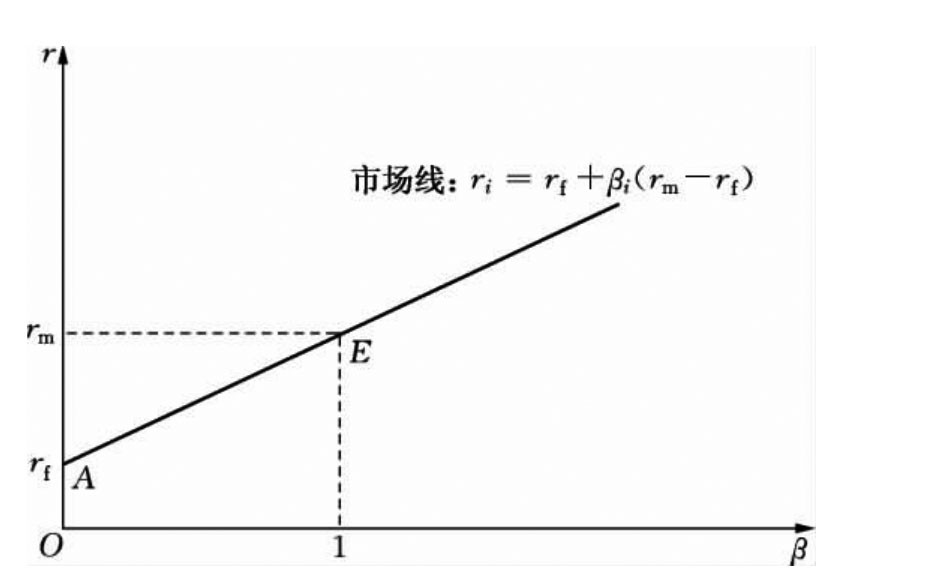
图11.11　风险资产的市场线

市场线的斜率显然等于（r_m－r_f），市场线表明了：在风险资本市场均衡条件下，风险资产期望收益率与市场风险之间存在着一种线性关系。市场线AE上的点表明风险资产交易市场均衡，在E点上，风险资产获得整个市场的期望收益均值r_m，此时的相对风险度为1。

CAPM也有诸多假定，如每个人对所有风险资产有统一认识、市场有效、投资人理性等等，它主要从需求方面分析风险资产定价问题，从供给角度分析风险资产定价的模型还有套利定价理论（arbitrage pricing theory，简称APT），有兴趣的同学可以在课下深入学习证券投资学或金融学等有关专业课程中的内容，我们这里就不再介绍了。