【摘要】:函数极限的定义: : 设函数在点的某一去心邻域有定义,如果存在常数A,对于任意给定的正数,总存在着正数,当时,有,则A就叫做函数当时的极限,记作:。数列极限的性质 唯一性: 如果数列收敛,那么它的极限唯一。局部保号性: 1) 如果,且(或),那么存在常数,使得当时,有(或)。
(1/3) 极限的定义
(1)数列极限的定义: 设 为一数列,若存在常数
为一数列,若存在常数 ,对于任意给定的
,对于任意给定的![]() ,存在正整数
,存在正整数![]() ,当
,当 时,有
时,有 ,则称数列
,则称数列 收敛于
收敛于 ,记为
,记为 。 (2)函数极限的定义(分两种情况): (i)
。 (2)函数极限的定义(分两种情况): (i) : 设函数
: 设函数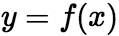 在点
在点![]() 的某一去心邻域有定义,如果存在常数A,对于任意给定的正数
的某一去心邻域有定义,如果存在常数A,对于任意给定的正数![]() ,总存在着正数
,总存在着正数![]() ,当
,当 时,有
时,有 ,则A就叫做函数
,则A就叫做函数 当
当 时的极限,记作:
时的极限,记作: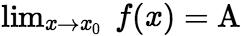 。 (ii)
。 (ii)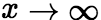 : 设函数
: 设函数 当
当![]() 大于某一正数时有定义,如果存在常数A,对于任意给定的正数
大于某一正数时有定义,如果存在常数A,对于任意给定的正数![]() ,总存在着正数X,当满足
,总存在着正数X,当满足 时,有
时,有 ,则A就叫做函数
,则A就叫做函数 当
当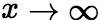 时的极限,记作:
时的极限,记作: 。
。
(2/3) 极限的基本性质
(1)数列极限的性质 (i)唯一性: 如果数列 收敛,那么它的极限唯一。 (ii)有界性: 如果数列
收敛,那么它的极限唯一。 (ii)有界性: 如果数列 收敛,那么数列
收敛,那么数列 一定有界(反之不成立)。 (iii)保号性: 如果
一定有界(反之不成立)。 (iii)保号性: 如果 ,且
,且![]() (或
(或![]() ),那么存在正整数
),那么存在正整数![]() ,当
,当 时,都有
时,都有 (或
(或 )。 推论:如果数列
)。 推论:如果数列 从某项起有
从某项起有 (或
(或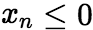 ),且
),且 ,那么
,那么![]() (或
(或![]() )。 (2)函数极限的性质 (i)唯一性: 如果
)。 (2)函数极限的性质 (i)唯一性: 如果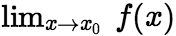 存在,那么这极限唯一。 (ii)有界性: 如果
存在,那么这极限唯一。 (ii)有界性: 如果 ,那么存在常数
,那么存在常数 和
和![]() ,使得当
,使得当 时,有
时,有 。 (iii)局部保号性: 1) 如果
。 (iii)局部保号性: 1) 如果 ,且
,且![]() (或
(或![]() ),那么存在常数
),那么存在常数![]() ,使得当
,使得当 时,有
时,有 (或
(或 )。 2) 如果
)。 2) 如果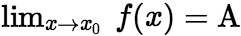 ,如果存在常数
,如果存在常数![]() ,使得当
,使得当 时,有
时,有 (或
(或 ),则
),则 (或
(或 )。
)。
(3/3) 极限存在充要条件
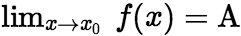
 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














