(1/6) 定积分的定义
设函数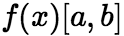 上有界,在
上有界,在![]() 中任意插入若干个分点
中任意插入若干个分点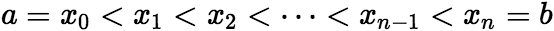 ,把区间
,把区间![]() 分成
分成 个小区间
个小区间


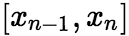 ,各个小区间的长度依次为
,各个小区间的长度依次为

 。在每个小区间[
。在每个小区间[ ]上任取一点
]上任取一点 ),作函数值
),作函数值 与小区间长度
与小区间长度![]() 的乘积
的乘积 并作和
并作和 。记
。记 ,如果不论对
,如果不论对![]() 怎样分法,也不论在小区间[
怎样分法,也不论在小区间[ ]上点
]上点 怎样取法,只要当
怎样取法,只要当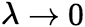 时,和
时,和![]() 总趋于确定的极限
总趋于确定的极限![]() ,这时我们称这个极限
,这时我们称这个极限![]() 为函数
为函数![]() 在区间
在区间![]() 上的定积分(简称积分),记作
上的定积分(简称积分),记作![]()
 。即
。即  =
=![]() =
= 。 其中
。 其中![]() 叫做被积函数,
叫做被积函数,![]() 叫做被积表达式,
叫做被积表达式,![]() 叫做积分变量,
叫做积分变量, 叫做积分下限,
叫做积分下限,![]() 叫做积分上限,
叫做积分上限,![]() 叫做积分区间。
叫做积分区间。
(2/6) 定积分的几何意义
设 在
在![]() 上连续,
上连续, 表示介于曲线
表示介于曲线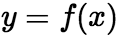 、
、![]() 轴、直线
轴、直线 及
及![]() 各部分面积的代数和。
各部分面积的代数和。
(3/6) 可积的必要条件
若函数![]() 在
在![]() 上可积,则
上可积,则![]() 在
在![]() 上必有界.
上必有界.
(4/6) 可积的充分条件
(1)若函数![]() 在
在![]() 上连续,则
上连续,则![]() 在
在![]() 上可积. (2)若函数
上可积. (2)若函数![]() 在区间
在区间![]() 上有界,且只有有限个间断点,则
上有界,且只有有限个间断点,则![]() 在
在![]() 上可积;或函数
上可积;或函数![]() 在
在![]() 上只有有限个第一类间断点,则
上只有有限个第一类间断点,则![]() 在
在![]() 上可积. (3)分段连续函数是可积的. (4)若
上可积. (3)分段连续函数是可积的. (4)若![]() 是
是![]() 上的单调有界函数,则
上的单调有界函数,则![]() 在
在![]() 上可积. 也就是说,单调有界函数,即使有无穷多个间断点,但这些不连续的点若存在一个极限点,则
上可积. 也就是说,单调有界函数,即使有无穷多个间断点,但这些不连续的点若存在一个极限点,则![]() 在
在![]() 上可积. (5)初等函数在其定义区间内的任一子区间上都是可积的.
上可积. (5)初等函数在其定义区间内的任一子区间上都是可积的.
(5/6) 定积分性质及定理
(1)函数和(差)的定积分等于它们的定积分的和(差),即  。 (2)被积函数的常数因子可以提到积分号外面,即
。 (2)被积函数的常数因子可以提到积分号外面,即 (
(![]() 是常数)。 (3)如果将积分区间分成两部分,则在整个区间上的定积分等于这两个区间上定积分之和,即设
是常数)。 (3)如果将积分区间分成两部分,则在整个区间上的定积分等于这两个区间上定积分之和,即设 ,则
,则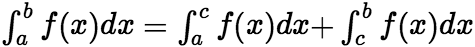 。 (4)如果在区间
。 (4)如果在区间![]() 上,
上,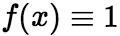 ,则
,则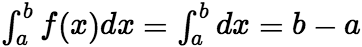 。 (5)如果在区间
。 (5)如果在区间![]() 上,
上, ,则
,则
 。 (6)如果在
。 (6)如果在![]() 上,
上,
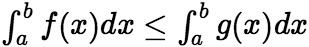
 。 特别的
。 特别的
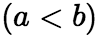 (7)设
(7)设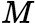 与
与![]() 分别是函数
分别是函数 上的最大值及最小值,则
上的最大值及最小值,则 
 。 (8)(定积分中值定理)如果函数
。 (8)(定积分中值定理)如果函数![]() 在闭区间
在闭区间![]() 上连续,则在积分区间
上连续,则在积分区间![]() 上至少存在一点
上至少存在一点![]() ,使下式成立:
,使下式成立:
 。
。
(6/6) 定积分的计算与技巧
(1)牛顿-莱布尼茨公式: 设![]() 在区间
在区间![]() 上连续,
上连续, 是
是![]() 在区间
在区间![]() 上的一个原函数,则
上的一个原函数,则  此公式被称为牛顿-莱布尼茨公式,它进一步揭示了定积分与原函数之间的联系,它给定积分提供了一个有效而简便的计算方法。 此外牛顿-莱布尼茨公式有如下推广: (i)设
此公式被称为牛顿-莱布尼茨公式,它进一步揭示了定积分与原函数之间的联系,它给定积分提供了一个有效而简便的计算方法。 此外牛顿-莱布尼茨公式有如下推广: (i)设![]() 在区间
在区间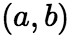 上连续,
上连续, 是
是![]() 在区间
在区间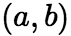 上的一个原函数,又
上的一个原函数,又 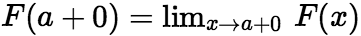 ,
, 都存在,则
都存在,则 
 (ii)设
(ii)设![]() 在区间
在区间![]() 上连续,
上连续, 在
在![]() 中除去
中除去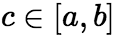 连续,
连续,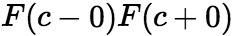 存在,且
存在,且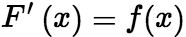 ,
, ,
,![]() ,则
,则 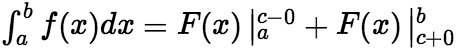
 (2)换元积分法: 设函数
(2)换元积分法: 设函数![]() 在区间
在区间![]() 上连续;函数
上连续;函数 在区间
在区间![]() 上是单值的且有连续导数;当t在区间
上是单值的且有连续导数;当t在区间![]() 上变化时,
上变化时,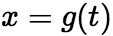 的值在
的值在![]() 上变化,且
上变化,且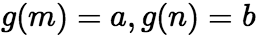 ;则有定积分的换元公式:
;则有定积分的换元公式: 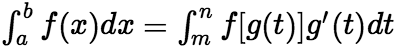 (3) 分部积分法 依据不定积分的分部积分,可以推算出
(3) 分部积分法 依据不定积分的分部积分,可以推算出 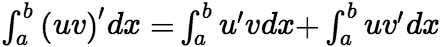 ,
,  ,
,
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















