(1/4) 反常积分的定义
(1)无穷限的广义积分: (i)积分区间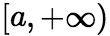 情形 设函数
情形 设函数![]() 在区间
在区间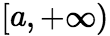 上连续,取
上连续,取![]() .如果极限
.如果极限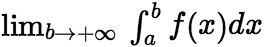 存在,则称此极限为函数
存在,则称此极限为函数![]() 在无穷区间
在无穷区间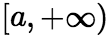 上的广义积分,记作
上的广义积分,记作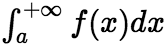 ,即
,即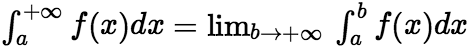 ,这时称广义积分
,这时称广义积分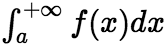 收敛;如果上述极限不存在,就称为广义积分
收敛;如果上述极限不存在,就称为广义积分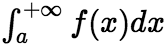 发散。 (ii)积分区间
发散。 (ii)积分区间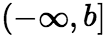 情形 设函数
情形 设函数![]() 在区间
在区间 上连续,取
上连续,取![]() ,如果极限
,如果极限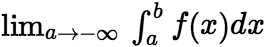 存在,则称此极限为函数
存在,则称此极限为函数![]() 在无穷区间
在无穷区间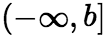 上的广义积分,记作
上的广义积分,记作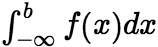 ,即
,即 ,这时称广义积分
,这时称广义积分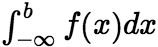 收敛;如果上述极限不存在,就称广义积分
收敛;如果上述极限不存在,就称广义积分 发散。 (iii)积分区间
发散。 (iii)积分区间 情形 设函数
情形 设函数![]() 在区间
在区间 上连续,如果广义积分
上连续,如果广义积分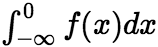 和
和 都收敛,则称上述两广义积分之和为函数
都收敛,则称上述两广义积分之和为函数![]() 在无穷区间(
在无穷区间( )上的广义积分,记作
)上的广义积分,记作 ,即
,即
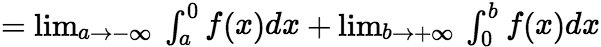 这时称广义积分
这时称广义积分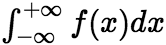 收敛;否则就称广义积分
收敛;否则就称广义积分 发散。 (2)无界函数的广义积分(也称瑕积分): (i)瑕点的定义:设
发散。 (2)无界函数的广义积分(也称瑕积分): (i)瑕点的定义:设![]() 在
在 上有定义,而
上有定义,而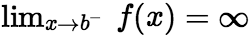 ,称b为
,称b为![]() 的瑕点。 (ii)瑕积分的定义: 设
的瑕点。 (ii)瑕积分的定义: 设![]() 在
在 上有定义,
上有定义,![]() 为瑕点,且对任意的
为瑕点,且对任意的![]() ,
,![]() 在
在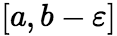 上可积,即极限
上可积,即极限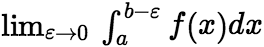 存在,则称该极限值为无界函数
存在,则称该极限值为无界函数![]() 在
在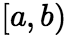 上的广义积分或叫瑕积分,记作:
上的广义积分或叫瑕积分,记作: 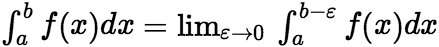 或
或 , 此时也称广义积分
, 此时也称广义积分 是收敛的;若上式的极限不存在,则称广义积分
是收敛的;若上式的极限不存在,则称广义积分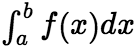 发散。 类似地可以定义瑕点为
发散。 类似地可以定义瑕点为 时的广义积分
时的广义积分 ,其中
,其中![]() 在
在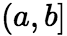 上有定义,
上有定义,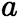 为瑕点,且在任何
为瑕点,且在任何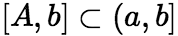 上可积。
上可积。
(2/4) 反常积分(广义积分)的性质及定理
(1)无穷限的广义积分: (i)若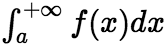 收敛,则
收敛,则 ,
,![]() 为常数. (ii)若
为常数. (ii)若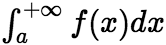 ,
, 都收敛,则
都收敛,则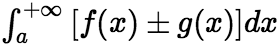 也收敛,且有
也收敛,且有 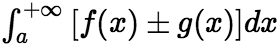
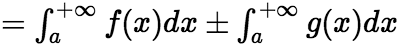 (iii)设
(iii)设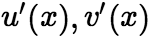 在
在 上连续,如果下面等式中有两项存在,则第三项也存在,且有
上连续,如果下面等式中有两项存在,则第三项也存在,且有  . (iv)若
. (iv)若![]() 在任何有限区间
在任何有限区间![]() 上可积,且
上可积,且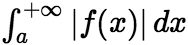 收敛,则
收敛,则 也收敛,且有
也收敛,且有 . (2)无界函数的广义积分: (i)若
. (2)无界函数的广义积分: (i)若 为瑕点且积分
为瑕点且积分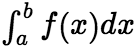 收敛,则
收敛,则 也收敛,且有
也收敛,且有 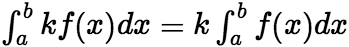 ,其中
,其中![]() 为常数。 (ii)若
为常数。 (ii)若![]() 与
与![]() 的瑕点同为
的瑕点同为 ,且瑕积分
,且瑕积分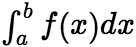 与
与 都收敛,则
都收敛,则  也收敛,且有
也收敛,且有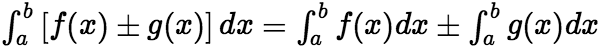 。 (iii)定积分的分部积分法与换元积分法对瑕积分也成立。 (iv)设
。 (iii)定积分的分部积分法与换元积分法对瑕积分也成立。 (iv)设 是
是![]() 的瑕点,
的瑕点,![]() 在
在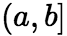 内的任一闭区间上可积,若积分
内的任一闭区间上可积,若积分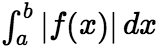 收敛,则
收敛,则 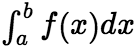 也收敛,且有
也收敛,且有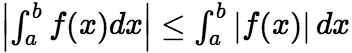 。
。
(3/4) 几个重要的反常积分(广义积分)
(1)若 则
则 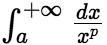
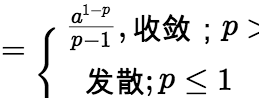 (2)若
(2)若 则
则 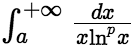
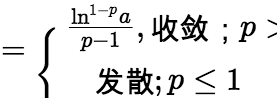 (3)若
(3)若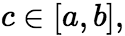 则
则  ,
, 时收敛;当
时收敛;当![]() 发散。 (4)若
发散。 (4)若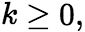 则
则 
 (5)
(5)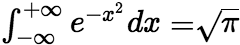 ;
; 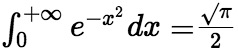
(4/4) 反常积分的计算与技巧
反常积分是变限积分的极限,因此由定积分的运算法则与极限运算法则就可得到反常积分的运算法则。下面以反常积分 为例,列出相应的运算法则,对于各种类型的反常积分也是有相应的计算法则。 (1)设
为例,列出相应的运算法则,对于各种类型的反常积分也是有相应的计算法则。 (1)设![]() 在区间
在区间 上连续,
上连续,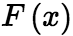 在
在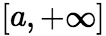 中连续,且
中连续,且
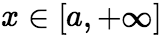 ,若
,若 存在,则反常积分
存在,则反常积分 收敛,且
收敛,且 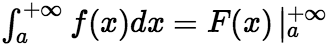
 若
若 不存在,则反常积分
不存在,则反常积分 发散。 (2)设
发散。 (2)设![]() ,
,![]() 在区间
在区间 上有连续的导数,若
上有连续的导数,若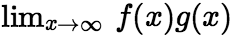 存在,且
存在,且 收敛,则
收敛,则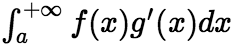 收敛,且
收敛,且 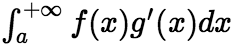
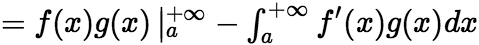 (3)设
(3)设![]() 在区间
在区间 上连续,
上连续,![]() 在
在![]() 中有连续的导数且单调,
中有连续的导数且单调, 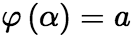 ,
,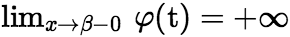 ,则
,则 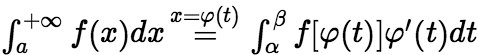 这里的
这里的![]() 可以是有限的,也可以是
可以是有限的,也可以是![]() 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















