【摘要】：由连续曲线及直线，，轴所围成的平面图形 绕轴旋转一周而成的旋转体的体积； 绕轴旋转一周而成的旋转体的体积。
(1/3) 平面图形的面积
（1）直角坐标情形： 设平面图形由上下两条曲线
与
及左右两条直线
与
所围成,则面积元素为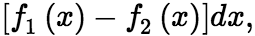
于是平面图形的面积为 
类似的，由左右两条曲线
与
及上下两条直线
与
所围成设平面图形的面积为 
注释：较为复杂图形的面积计算，可将图形分割若干小图形，使其符合
型或
型，然后求面积和。 （2）极坐标情形： 曲边扇形及曲边扇形的面积元素:由曲线
及射线
围成的图形称为曲边扇形.曲边扇形的面积元素为
曲边扇形的面积为
由连续曲线
和射线
所围成图形的面积
（3）曲线方程是参数方程形式的情况： 设曲线C的参数方程为
，
在
上具有连续导数，且
不变号，
且连续，则由曲线
和直线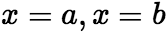
,
轴围成的平面图形的面积
(2/3) 体积
（1）旋转体的体积： （i）平面图形由曲线
与直线
，
，
轴所围成： 绕
轴旋转一周而成的旋转体的体积为
； 绕
轴旋转一周而成的旋转体的体积为
。 （ii）由连续曲线
及直线
，
，
轴所围成的平面图形 绕
轴旋转一周而成的旋转体的体积
； 绕
轴旋转一周而成的旋转体的体积
。 （2）已知平行截面面积的立体体积： 设在空间直角坐标系中，有一个立体夹在垂直于
轴的两个平行平面
与
之间，它被垂直
轴的平面截得的截面面积为
，且
在
上连续，则立体的体积 
.
(3/3) 平面曲线的弧长
（1）曲线为参数形式的平面曲线的弧长公式： 设曲线
是由参数方程
给出的光滑曲线，即
在
上具有连续的导数，则曲线段弧长为 
. （2）曲线方程为直角坐标方程的弧长公式： 设曲线
在
上是光滑曲线，则曲线段的弧长为
. （3）曲线方程为极坐标方程的弧长公式： 设曲线段是由极坐标方程
，
给出的光滑曲线，则曲线段的弧长为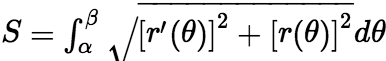 
.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
