(1/4) 偏导数的概念
(1)偏导数的定义 对于二元函数 如果只有自变量
如果只有自变量![]() 变化,而自变量
变化,而自变量![]() 固定,这时它就是
固定,这时它就是![]() 的一元函数,这函数对
的一元函数,这函数对![]() 的导数,就称为二元函数
的导数,就称为二元函数 对于
对于![]() 的偏导数. 设函数
的偏导数. 设函数 在点
在点 的某一邻域内有定义,当
的某一邻域内有定义,当![]() 固定在
固定在 而
而![]() 在
在![]() 处有增量
处有增量![]() 时,相应地函数有增量
时,相应地函数有增量 , 如果极限
, 如果极限 存在,则称此极限为函数
存在,则称此极限为函数 在点
在点 处对
处对![]() 的偏导数,记作
的偏导数,记作 ,
, ,
, ,或
,或 . 类似地,函数
. 类似地,函数 在点
在点 处对
处对![]() 的偏导数定义为
的偏导数定义为  , 记作
, 记作  ,
, ,
, ,或
,或 注:求
注:求 时,只要把
时,只要把![]() 暂时看作常量而对
暂时看作常量而对![]() 求导数;求
求导数;求![]() 时,只要把
时,只要把![]() 暂时看作常量而对
暂时看作常量而对![]() 求导数。 [例题]:求
求导数。 [例题]:求 的偏导数。 解:
的偏导数。 解: (2)偏导数的几何意义 由于
(2)偏导数的几何意义 由于 
 可见偏导数的几何意义为:曲线
可见偏导数的几何意义为:曲线 (曲面
(曲面 与平面
与平面 的交线)在点
的交线)在点 处的切线对
处的切线对![]() 轴的斜率。
轴的斜率。
(2/4) 偏导数的计算
(1)求偏导数,归结为求一元函数的导数。 (2)求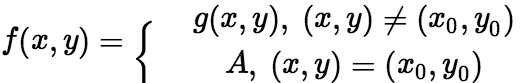 .在
.在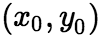 处的偏导数的方法: 按定义:
处的偏导数的方法: 按定义:

(3/4) 高阶偏导数
(1)二阶偏导数 函数 在区域
在区域![]() 内具有偏导数
内具有偏导数 ,
,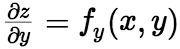 , 那么在
, 那么在![]() 内
内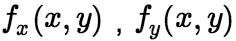 都是
都是![]() 的函数.如果这两个函数的偏导数也存在,则称它们是函数
的函数.如果这两个函数的偏导数也存在,则称它们是函数 的二阶偏导数.按照对变量求导次序的为同有下列四个二阶偏导数:
的二阶偏导数.按照对变量求导次序的为同有下列四个二阶偏导数:  ,
,  ,
,  ,
,  . (2)混合偏导数 根据上面所说的四个二阶偏导数中
. (2)混合偏导数 根据上面所说的四个二阶偏导数中  ,
,  称为混合偏导数. (3)同样可得三阶、四阶以及
称为混合偏导数. (3)同样可得三阶、四阶以及 阶偏导数.二阶及二阶以上的偏导数统称为高阶偏导数. (4)混合偏导数与求偏导的先后次序无关 若函数
阶偏导数.二阶及二阶以上的偏导数统称为高阶偏导数. (4)混合偏导数与求偏导的先后次序无关 若函数 的两个二阶混合偏导数
的两个二阶混合偏导数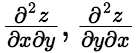 都在区域
都在区域![]() 上连续,则在区域
上连续,则在区域![]() 内,
内, ,即二阶混合偏导数与求偏导数的先后次序无关。
,即二阶混合偏导数与求偏导数的先后次序无关。
(4/4) 偏导数为零时的多元函数
(1)设 在区域
在区域![]() 满足
满足 ,则
,则 在区域
在区域![]() 为常数。 (2)设
为常数。 (2)设 定义在全平面上,若
定义在全平面上,若![]() ,则
,则 ;若
;若![]() ,则
,则 ,其中
,其中 均为任意的一元函数。
均为任意的一元函数。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















