【摘要】：极大值、极小值统称为极值. 使函数取得极值的点称为极值点. 驻点概念： 凡是能使同时成立的点称为的驻点。
(1/3) 多元函数极值及驻点
（1）极值概念： 设函数
在点
的某个邻域内有定义,如果对于该邻域内任何异于
的点
, 都有
(或
), 则称函数在点
有极大值(或极小值)
。 极大值、极小值统称为极值. 使函数取得极值的点称为极值点. （2）驻点概念： 凡是能使
同时成立的点
称为
的驻点。
(2/3) 多元函数取得极值的条件
（1）必要条件： 设函数
在点
具有偏导数,且在点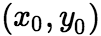
处有极值,则有
。 注：由上述条件可知具有偏导数的函数的极值点必定是驻点.但函数的驻点不一定是极值点，如函数
在原点处。 （2）充分条件： 设函数
在点
的某邻域内连续且有一阶及二阶连续偏导数,又
,令
,
,
则
在
处是否取得极值的条件如下: (1)
时具有极值,且当
时有极大值,当
时有极小值; (2)
时没有极值; (3)
时可能有极值,也可能没有极值.
(3/3) 求二元函数极值点的一般步骤
第一步 ：解方程组
,求得一切实数解,即可得一切驻点. 第二步 ：对于每一个驻点
,求出二阶偏导数的值
和
. 第三步 ：定出
的符号,按极值的充分条件判定
是否是极值、是极大值还是极小值.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
