【摘要】:对一切自然数,都有,称级数为正项级数。正项级数收敛的充分必要条件是:它的部分和数列有界。时,若级数收敛,则级数收敛;时,若级数发散,则级数发散。交错级数的收敛法通常利用莱布尼茨定理。
(1/3) 正项级数及其收敛法
对一切自然数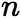 ,都有
,都有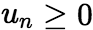 ,称级数
,称级数 为正项级数。正项级数
为正项级数。正项级数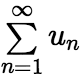 收敛的充分必要条件是:它的部分和数列
收敛的充分必要条件是:它的部分和数列 有界。 正项级数的收敛法有如下几种: (1)比较收敛法:设
有界。 正项级数的收敛法有如下几种: (1)比较收敛法:设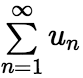 和
和![]() 都是正项级数,且
都是正项级数,且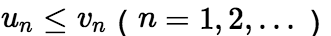 若级数
若级数![]() 收敛,则级数
收敛,则级数 收敛;若级数
收敛;若级数 发散,则
发散,则![]() 发散。 (2)比较收敛法的极限形式:若
发散。 (2)比较收敛法的极限形式:若
 ,则
,则 和
和![]() 同时收敛或同时发散。
同时收敛或同时发散。  时,若级数
时,若级数![]() 收敛,则级数
收敛,则级数 收敛;
收敛;  时,若级数
时,若级数![]() 发散,则级数
发散,则级数 发散。 (3)比值收敛法:若
发散。 (3)比值收敛法:若 ,则若
,则若![]() ,级数收敛;若
,级数收敛;若![]()
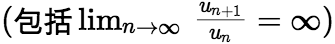 ,级数发散;当
,级数发散;当![]() 时,级数可能收敛,也可能发散。 (4) 根值收敛法:若
时,级数可能收敛,也可能发散。 (4) 根值收敛法:若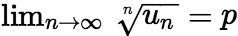 ,则若
,则若![]() ,级数收敛;若
,级数收敛;若![]()
 ,级数发散;当
,级数发散;当![]() 时,级数可能收敛,也可能发散。
时,级数可能收敛,也可能发散。
(2/3) 交错级数及其收敛法
交错级数:一个级数如果它的各项是正负交错的则称为交错级数。 交错级数的收敛法通常利用莱布尼茨定理。 设 为交错级数,若满足条件 (1)
为交错级数,若满足条件 (1) ; (2)
; (2) , 则级数
, 则级数 收敛,且其和
收敛,且其和![]() .,其余项
.,其余项![]() 的绝对值
的绝对值 。
。
(3/3) 绝对收敛与条件收敛
(1)绝对收敛与条件收敛定义: 若 收敛,则级数
收敛,则级数 绝对收敛;若
绝对收敛;若 收敛,而
收敛,而 发散,则级数
发散,则级数 条件收敛。 (2)绝对收敛的性质 绝对收敛的级数一定收敛,即
条件收敛。 (2)绝对收敛的性质 绝对收敛的级数一定收敛,即 收敛,则
收敛,则 收敛。 推论:一个绝对收敛级数的正数项与负数项所组成的级数都是收敛的; 一个条件收敛级数的正数项与负数项所组成的级数都是发散的。
收敛。 推论:一个绝对收敛级数的正数项与负数项所组成的级数都是收敛的; 一个条件收敛级数的正数项与负数项所组成的级数都是发散的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















