(1/4) 排列与逆序
(1)排列与n阶排列 所谓排列是指由n个数 所构成的一个有序数组,通常用
所构成的一个有序数组,通常用 表示n阶排列,显然有
表示n阶排列,显然有![]() 个不同的n阶排列。 (2)逆序与逆序数 在一个排列中,若较大的数在较小的数前面,这两个数就构成一个逆序。所有逆序数的总和称为这个排列的逆序数,记做
个不同的n阶排列。 (2)逆序与逆序数 在一个排列中,若较大的数在较小的数前面,这两个数就构成一个逆序。所有逆序数的总和称为这个排列的逆序数,记做 。 (3)奇排列与偶排列 逆序数为奇数的排列称为奇排列,逆序数是偶数的排列则称为偶排列。 (4)逆序数的计算方法 以 3 2 4 1 5为例,从第一个数依次查起,分别计算出排列中每个元素前面比它大的数码个数之和,即算出排列中每个元素的逆序数,这每个元素的逆序数之总和即为所求排列的逆序数. (5)对换 将一个排列中的某两个数的位置互换而其余的数不动,这一变换即为一次对换。 (6)排列的性质 (i)对排列进行一次对换将改变其奇偶性. (ii)在全体n阶排列(n>1)中,奇排列和偶排列各占一半,各有
。 (3)奇排列与偶排列 逆序数为奇数的排列称为奇排列,逆序数是偶数的排列则称为偶排列。 (4)逆序数的计算方法 以 3 2 4 1 5为例,从第一个数依次查起,分别计算出排列中每个元素前面比它大的数码个数之和,即算出排列中每个元素的逆序数,这每个元素的逆序数之总和即为所求排列的逆序数. (5)对换 将一个排列中的某两个数的位置互换而其余的数不动,这一变换即为一次对换。 (6)排列的性质 (i)对排列进行一次对换将改变其奇偶性. (ii)在全体n阶排列(n>1)中,奇排列和偶排列各占一半,各有 个。 (iii)任意一个n阶排列都可以经过一系列对换互换得到
个。 (iii)任意一个n阶排列都可以经过一系列对换互换得到 ,并且所作的对换的个数与这个排列有相同的奇偶性。
,并且所作的对换的个数与这个排列有相同的奇偶性。
(2/4) n阶行列式
n阶行列式

是所有取各自不同行不同列的n个元素的乘积  的代数和,其中
的代数和,其中 是
是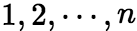 的一个排列。当
的一个排列。当 是偶排列时,上式带有正号;当
是偶排列时,上式带有正号;当 是奇排列时,上式带有负号,也就是可写成
是奇排列时,上式带有负号,也就是可写成 
 上式称为n阶行列式的完全展开式,这里
上式称为n阶行列式的完全展开式,这里 表示对所有 级排列求和。行列式 通常可简记为
表示对所有 级排列求和。行列式 通常可简记为 或
或 。 例题:设
。 例题:设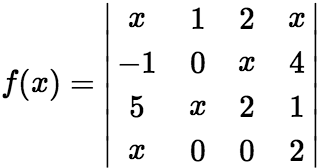 ,则
,则 中,
中,![]() 的系数是__ 根据行列式的定义,不同同行不同列的4个元素的乘积为
的系数是__ 根据行列式的定义,不同同行不同列的4个元素的乘积为![]() 当且仅当
当且仅当 时成立,而该项在行下标顺排时,列的下标的逆序数为
时成立,而该项在行下标顺排时,列的下标的逆序数为 ,则该项为
,则该项为 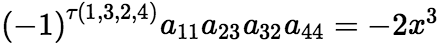 故
故![]() 的系数为-2。
的系数为-2。
(3/4) 行列式的性质
(1)行列式与它的转置行列式相等,即  。 证明 : 记
。 证明 : 记 ,则其转置行列式为
,则其转置行列式为 因为
因为![]() 中元素
中元素![]() 位于
位于 的第
的第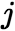 行第
行第 列,所以
列,所以 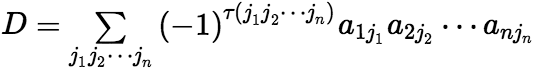
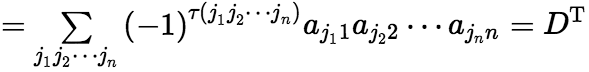 (2)任意对换行列式的两行(或两列)元素,其值变号。 注:行列式中有两行(或两列)元素对应相同,则此行列式为零 (3)行列式的某一行(列)的所有元素都乘以同一数k,等于用数k乘此行列式。 即
(2)任意对换行列式的两行(或两列)元素,其值变号。 注:行列式中有两行(或两列)元素对应相同,则此行列式为零 (3)行列式的某一行(列)的所有元素都乘以同一数k,等于用数k乘此行列式。 即 
 注:行列式中某一行(列)的所有元素的公因子可以得到行列式几号的外面。 (4)行列式中如果两行(列)元素成比例,则此行列式等于零。 (5)行列式中如果某一行(列)的元素都是两组数之和,那么这个行列式就等于两个行列式之和。 即
注:行列式中某一行(列)的所有元素的公因子可以得到行列式几号的外面。 (4)行列式中如果两行(列)元素成比例,则此行列式等于零。 (5)行列式中如果某一行(列)的元素都是两组数之和,那么这个行列式就等于两个行列式之和。 即
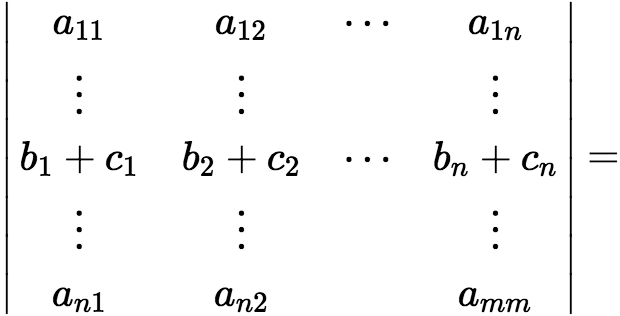
 (6)把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去,行列式不变。 即
(6)把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去,行列式不变。 即 

(4/4) 2017线性代数基础课程导学
主讲老师:姜晓千 中国人民大学金融数学博士,多年考研辅导经验,对历年真题有着极其深入地研究,授课风格高屋建瓴、激情洋溢、亲和幽默,深受广大考生喜爱。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















