(1/8) 矩阵的加法
(1)定义 设 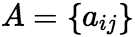 和
和  是
是  的矩阵,A与B的加法(或称和),记作A + B ,规定为:
的矩阵,A与B的加法(或称和),记作A + B ,规定为: 
 注:只有当两个矩阵是同型矩阵时,这两个矩阵才能进行加法运算 (2)加法的运算法则 (i)
注:只有当两个矩阵是同型矩阵时,这两个矩阵才能进行加法运算 (2)加法的运算法则 (i) (ii)
(ii) (3)矩阵减法 设矩阵
(3)矩阵减法 设矩阵 ,记
,记 ,
,![]() 称为矩阵A的负矩阵,显然有
称为矩阵A的负矩阵,显然有 由此规定矩阵的减法为
由此规定矩阵的减法为  即:
即:

(2/8) 矩阵数乘
(1)定义 数![]() 与矩阵
与矩阵 的乘积(称之为数乘),记作
的乘积(称之为数乘),记作![]() 或
或![]() ,规定为
,规定为 
 (2)数乘矩阵的运算规律 (i)
(2)数乘矩阵的运算规律 (i) (ii)
(ii) (iii)
(iii)
(3/8) 矩阵与矩阵相乘
(1)定义 设 是一个
是一个 矩阵,
矩阵, 是一个
是一个![]() 矩阵,那么规定矩阵A与矩阵B的乘积为一个
矩阵,那么规定矩阵A与矩阵B的乘积为一个 的矩阵
的矩阵  ,其中
,其中 
 . 并把此乘积记作
. 并把此乘积记作  注:(i)只有在左矩阵A的列数和右矩阵B的行数相等时,才能定义乘法AB; (ii)矩阵C=AB的行数是A的行数,列数则是B的列数; (iii)矩阵C=AB在
注:(i)只有在左矩阵A的列数和右矩阵B的行数相等时,才能定义乘法AB; (ii)矩阵C=AB的行数是A的行数,列数则是B的列数; (iii)矩阵C=AB在![]() 位置上的元素等于A的第
位置上的元素等于A的第 行元素与B的第
行元素与B的第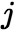 列对应元素的乘积之和。 (2)矩阵的幂 设
列对应元素的乘积之和。 (2)矩阵的幂 设![]() 是
是 阶矩阵,定义:
阶矩阵,定义:  , 其中,
, 其中,![]() 是正整数;特别规定
是正整数;特别规定 . 由于乘法成立分配律结合律,有
. 由于乘法成立分配律结合律,有 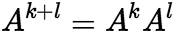 ,
, (3)矩阵相乘的注意事项 (i)矩阵乘法一般没有交换律,即
(3)矩阵相乘的注意事项 (i)矩阵乘法一般没有交换律,即 ,若对于两个n阶方阵A、B,
,若对于两个n阶方阵A、B, ,则称A与B是可交换的; (ii)不可将关于数的代数恒等式或命题等价到矩阵相乘,例如,设A,B,C均为n阶方阵,则
,则称A与B是可交换的; (ii)不可将关于数的代数恒等式或命题等价到矩阵相乘,例如,设A,B,C均为n阶方阵,则  ;
; ;
;  (k为自然数);
(k为自然数); 上述关系当且仅当矩阵A与B可交换才成立; (iii)
上述关系当且仅当矩阵A与B可交换才成立; (iii) 不是一定有
不是一定有![]() 或
或![]() ;若
;若![]() ,而
,而 ,不能得出
,不能得出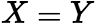 ;矩阵
;矩阵 ,但
,但 有可能成立。 (4)矩阵相乘的运算法则 (i)
有可能成立。 (4)矩阵相乘的运算法则 (i) (ii)
(ii) (其中
(其中![]() 为数) (iii)
为数) (iii) ,
, (5)重要公式
(5)重要公式 
(4/8) 矩阵转置的运算规律
(1) ; (2)
; (2) ; (3)
; (3) 是常数; (4)
是常数; (4) 例题:设列矩阵
例题:设列矩阵 满足
满足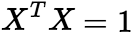 ,E为n阶单位阵,
,E为n阶单位阵, ,证明H是对称阵,且
,证明H是对称阵,且 。 证明过程如下:
。 证明过程如下: 
 所以H是对称阵。
所以H是对称阵。 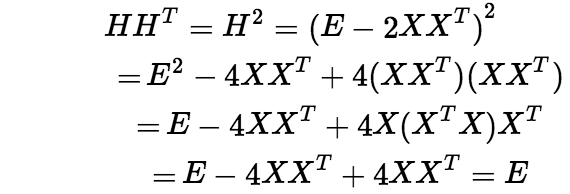
(5/8) 方阵的行列式的运算规律
(1)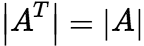 (2)
(2) (3)
(3) 注:对于n阶矩阵A,B一般来说
注:对于n阶矩阵A,B一般来说 ,但总有
,但总有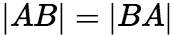
(6/8) 共轭矩阵的运算规律
(1) (2)
(2) (3)
(3)
(7/8) 关于伴随矩阵的运算规律
(1)设A是n阶方阵,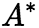 是A的伴随矩阵,则
是A的伴随矩阵,则  (2)
(2) (3)
(3) (4)
(4) ; (5)
; (5) (6)若A可逆,则
(6)若A可逆,则

(8/8) 分块矩阵的运算法则
(1)定义 矩阵分块是将矩阵用任意的横线和纵线切开,例如  ,下面给出它的三种分法, (i)
,下面给出它的三种分法, (i) ;令
;令 ,
, ,
, ,
, ,则
,则 。 (ii)
。 (ii) ;令
;令 ,
, ,
,  ,
, ,
, ,
, 。 则
。 则 。 (iii)
。 (iii) 。令
。令 ,
, ,
,  ,
, ,则
,则 。 (2) 关于分块矩阵的运算法则 (i)
。 (2) 关于分块矩阵的运算法则 (i) 
 (ii)
(ii) 
 (iii)
(iii)  (iv)
(iv)  (v)
(v) 
 (vi) 如果AB=C,其中A是
(vi) 如果AB=C,其中A是 矩阵,B是
矩阵,B是![]() 矩阵,那么对矩阵B,C按行分块有
矩阵,那么对矩阵B,C按行分块有 
 可见矩阵AB行向量
可见矩阵AB行向量 可由B的行向量
可由B的行向量 线性表出。 类似的,对矩阵A,C按列分块,有
线性表出。 类似的,对矩阵A,C按列分块,有  即
即 说明矩阵AB的列向量
说明矩阵AB的列向量 可由A的列向量
可由A的列向量 线性表出。
线性表出。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














