第节，矩阵

(1/2) 矩阵及其相关概念

（1）矩阵 由个数 （i = 1, 2, …, m ，j = 1, 2, …, n ），排成m行n列的数表  称为m行n列矩阵，简称为矩阵，简记为A，也记为或。若m=n，则称A是n阶矩阵或n阶方阵。当  时，即，此时矩阵退化为一个数 。 注：（i）切记不允许使用 （ii）当矩阵元素全为实数时，此矩阵称为实矩阵。 （iii）只有一行的矩阵称为行矩阵，又称行向量；同理，只有一列的矩阵称为列矩阵，又称列向量。 （2）同型矩阵 矩阵如果m=s，n=t则称A与B是同型矩阵。 （3）零矩阵 所有元素都是零的矩阵称为零矩阵，记做。 （4）矩阵相等 若同型矩阵和在对应位置上的元素都相等，即  则称矩阵A与B相等，记做A = B。 （5）方阵的行列式 对于n阶矩阵，其元素可构造n阶行列式  称为方阵A的行列式，记作 。 注：矩阵的行列式与矩阵是两个不同的概念，前者是一个数，后者是一个数表。

(2/2) 特殊矩阵

（1）单位矩阵 主对角线上元素全为1，其余元素均为0的n阶方阵，称为n阶单位矩阵，即 。 （2）转置矩阵 设，是将A的行和列对应互换得到的矩阵，称它为A的转置矩阵，记作。 （3）对称矩阵 如果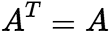，即，则A是对称矩阵 （4）反对称矩阵 如果，即，则A是反对称矩阵。 注：若A、B是同阶的（反）对称矩阵，则也是（反）对称矩阵，但AB不一定是（反）对称矩阵。 （5）伴随矩阵 设是n阶方阵，由行列式 || 中的每个元素的代数余子式所构成的矩阵  称之为矩阵的伴随矩阵。记为。 注意：伴随矩阵在位置上的元素是矩阵在位置上的代数余子式。 （6）对角矩阵 设A是n阶矩阵，如，则称其为对角矩阵，记为。 注：同阶的对角矩阵的和、差、积仍是对角矩阵。 （7）逆矩阵 设是阶矩阵，若存在矩阵，使得 ， 则称是可逆矩阵，并称矩阵是的逆矩阵；A的逆矩阵唯一，记作。 （8）正交矩阵 设A是n阶矩阵，如,则称A是正交矩阵。 注：A是正交矩阵等价于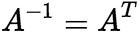. （9）共轭矩阵 当为复矩阵时，用表示的共轭复数，记，称为A的共轭矩阵。