(1/3) 向量组的线性相关
(1)线性相关定义: 对于m维向量组A : ,若存在不全为零的数
,若存在不全为零的数 ,使得
,使得 ,则称向量组A线性相关. (2)线性相关性的判定 向量组
,则称向量组A线性相关. (2)线性相关性的判定 向量组 线性相关
线性相关![]() (i)齐次方程组
(i)齐次方程组 *有非零解。 证明:记
*有非零解。 证明:记
 ,*式等价于:
,*式等价于: 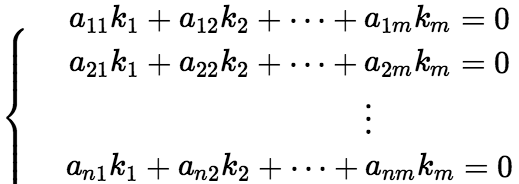 (**) 因而有,向量组A :
(**) 因而有,向量组A : 线性相关的充要条件是齐次线性方程(**)有非零解。 (ii)向量组的秩
线性相关的充要条件是齐次线性方程(**)有非零解。 (ii)向量组的秩 (向量组的个数) (iii)存在某
(向量组的个数) (iii)存在某![]() (i=1,2,...,s)可由其余
(i=1,2,...,s)可由其余 个向量线性表出。 证明:充分性:设向量组A :
个向量线性表出。 证明:充分性:设向量组A : 线性相关,则存在不全为零的数
线性相关,则存在不全为零的数 ,使得
,使得 ,不妨设
,不妨设![]() ,有
,有  即
即![]() 可由
可由![]() 、
、![]() 、… 、
、… 、![]() 线性表示。 必要性:已知向量组A中至少有一个向量可由其余m -1个向量线性表示,不妨设
线性表示。 必要性:已知向量组A中至少有一个向量可由其余m -1个向量线性表示,不妨设![]() 可由
可由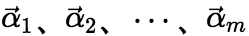 线性表示。即存在
线性表示。即存在 使得
使得  ,从而有
,从而有
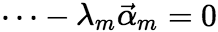 ,即向量组A :
,即向量组A : 线性相关,这是可认为取
线性相关,这是可认为取 。 (3)线性相关的性质 (i)含有零向量的向量组一定线性相关。 (ii)只有一个向量的向量组线性相关的充要条件是这个向量是零向量。 (iii)只有两个向量的向量组线性相关的充要条件是这两个向量的坐标对应成比例。个数多于维数的向量组必线性相关。 (iv)向量组中的部分向量线性相关,则原向量组线性相关;向量组线性无关,则它的部分向量也线性无关。 (v)如果r维向量组线性无关,将此向量组扩展到
。 (3)线性相关的性质 (i)含有零向量的向量组一定线性相关。 (ii)只有一个向量的向量组线性相关的充要条件是这个向量是零向量。 (iii)只有两个向量的向量组线性相关的充要条件是这两个向量的坐标对应成比例。个数多于维数的向量组必线性相关。 (iv)向量组中的部分向量线性相关,则原向量组线性相关;向量组线性无关,则它的部分向量也线性无关。 (v)如果r维向量组线性无关,将此向量组扩展到 维后的向量组也线性无关。
维后的向量组也线性无关。
(2/3) 向量组的线性无关
(1)线性无关的定义: 对于向量组 ,如果
,如果 ,必有
,必有 ,则称向量组
,则称向量组 线性无关。或者说,只要
线性无关。或者说,只要 不全为零,必有
不全为零,必有 ,则称向量组
,则称向量组 线性无关。 (2)线性无关的判定: 向量组
线性无关。 (2)线性无关的判定: 向量组 线性无关
线性无关![]() (i) 齐次方程组
(i) 齐次方程组 只有零解。 (ii)向量组的秩
只有零解。 (ii)向量组的秩 (向量组的个数) (iii)每一个向量
(向量组的个数) (iii)每一个向量![]() (i=1,2,...,m)都不能用其余s-1个向量线性表出。 (3)线性无关的性质: (i)若向量组
(i=1,2,...,m)都不能用其余s-1个向量线性表出。 (3)线性无关的性质: (i)若向量组 线性无关,则它的任一个部分组
线性无关,则它的任一个部分组 必线性无关。 (ii)若向量组
必线性无关。 (ii)若向量组 线性无关,则它的任一延伸组
线性无关,则它的任一延伸组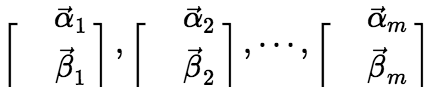 必线性无关。 (iii)阶梯形向量组一定线性无关。 (iv)两两正交、非零的向量组必线性无关。
必线性无关。 (iii)阶梯形向量组一定线性无关。 (iv)两两正交、非零的向量组必线性无关。
(3/3) 线性相关性与线性表出的关系
(1)向量组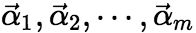 线性无关,而向量组
线性无关,而向量组 线性相关,则
线性相关,则![]() 可由
可由 线性表出,且表示法唯一。 (2)若向量组
线性表出,且表示法唯一。 (2)若向量组 可由向量组
可由向量组 线性表出,且
线性表出,且 ,则
,则 线性相关。 注:多数向量可由少数向量线性表出,则多数向量线性相关。 (3)若向量组
线性相关。 注:多数向量可由少数向量线性表出,则多数向量线性相关。 (3)若向量组 可由向量组
可由向量组 线性表出,且
线性表出,且 线性无关,则
线性无关,则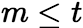 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















