【摘要】:设A是矩阵,齐次方程组有非零解的充分必要条件是,亦即A的列向量线性相关。如A是n阶矩阵,有非零解的充要条件是. 有非零解的充分条件是。
1/4) 齐次方程组有非零解的判定
(1)设A是 矩阵,齐次方程组
矩阵,齐次方程组 有非零解的充分必要条件是
有非零解的充分必要条件是 ,亦即A的列向量线性相关。 (2)如A是n阶矩阵,
,亦即A的列向量线性相关。 (2)如A是n阶矩阵,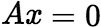 有非零解的充要条件是
有非零解的充要条件是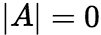 . (3)
. (3)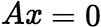 有非零解的充分条件是
有非零解的充分条件是 (即方程个数<未知数个数)。 注:齐次方程组有非零解,关键在于系数矩阵的秩要小于未知数的个数(也就是系数矩阵中列向量的个数),(2)用行列式判定解是有条件的,而(3)反映的是n+1个n维向量必线性相关。 (4)如
(即方程个数<未知数个数)。 注:齐次方程组有非零解,关键在于系数矩阵的秩要小于未知数的个数(也就是系数矩阵中列向量的个数),(2)用行列式判定解是有条件的,而(3)反映的是n+1个n维向量必线性相关。 (4)如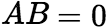 则
则![]() 的每一列都是
的每一列都是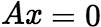 的解,当
的解,当![]() 时,蕴含
时,蕴含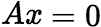 有非零解,进而有
有非零解,进而有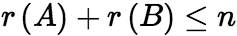 .
.
(2/4) 非齐次方程组有解的判定
(1)增广矩阵 设有n个未知数m个方程的非齐次线性方程组: 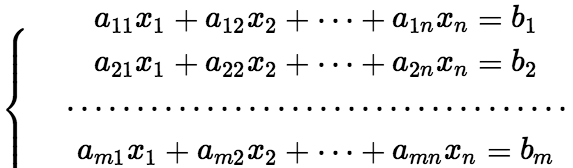 令
令 ,
,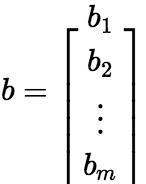 ,
, ,
, 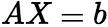 定义增广矩阵:
定义增广矩阵: 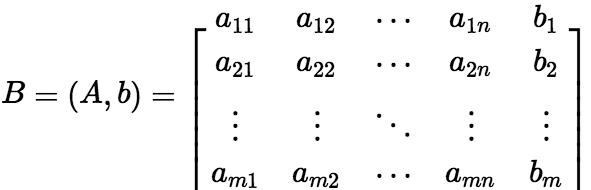 (2)设A是
(2)设A是 矩阵,方程组
矩阵,方程组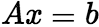 ,则 (i)有唯一解
,则 (i)有唯一解 ![]()
 (ii)有无穷多解
(ii)有无穷多解 ![]()
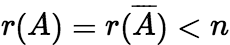 (iii)无解
(iii)无解 ![]()
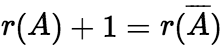
![]() b不能由A的列向量线性表出
b不能由A的列向量线性表出
(3/4) 齐次方程组和非齐次方程组解的关系
(1)如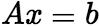 有唯一解,则
有唯一解,则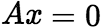 只有零解。 (2)当
只有零解。 (2)当 只有零解,
只有零解, 没有无穷多解,也就是可能有唯一解也可能无解。
没有无穷多解,也就是可能有唯一解也可能无解。
(4/4) 方程组解的性质
(1)若 是
是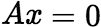 的解,则
的解,则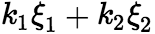 是
是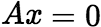 的解 (2)若
的解 (2)若![]() 是
是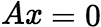 的解,
的解,![]() 是
是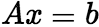 的解,则
的解,则![]() 是
是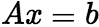 的解; (3)若
的解; (3)若![]() 是
是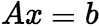 的解,则
的解,则 是
是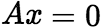 的解. 推广: (1)设
的解. 推广: (1)设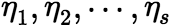 是
是 的解,则当
的解,则当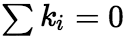 时
时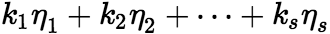 为
为 的解;当
的解;当 时
时 为
为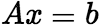 的解; (2)设
的解; (2)设 是
是 的s个线性无关的解,则
的s个线性无关的解,则 为
为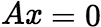 的s-1个线性无关的解.
的s-1个线性无关的解.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















