【摘要】：若n阶矩阵A与B相似，由，要联想到以下结论： ，。，进而可以用相似求方幂若，且A，B都可逆，则。
(1/3) 相似矩阵的概念
设A，B都是n阶矩阵，若存在可逆矩阵P，使得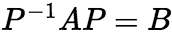
成立，则称B是A的相似矩阵，或说矩阵A与B相似，记作
。
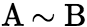(2/3) 相似矩阵的性质
（1）反身性 对任意的方阵
，
与
相似； （2）对称性 若
与
相似，则
与
相似； （3）传递性 若
与
相似，
与
相似，则
与
相似．
(3/3) 相似矩阵的相关结论
（1）相似矩阵的秩和行列式都相同． 证明：因为
与
相似，所以存在可逆矩阵
，使
，因此
，且
（2）相似矩阵有相同的可逆性，且可逆时其逆也相似． 证明： 由（1）有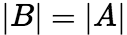
，所以它们的可逆性是相同的．设
与
相似，且
可逆，则
也可逆，且
即
与
相似． （3）若n阶矩阵A与B相似，则A与B具有相同的特征多项式，从而A与B有相同的特征值． 证明：因为A与B相似，所以有可逆矩阵P，使
，因此 
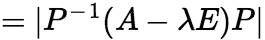
即A与B有相同的特征多项式。 推论：若n阶矩阵A与对角矩阵
相似，则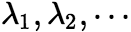
，
是A的n个特征值． （4）若n阶矩阵A与B相似，则A与B具有相同的迹（
）。 （5）若n阶矩阵A与B相似，由
，要联想到以下结论： （i）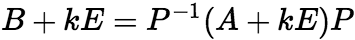
， 
。 （ii）
，进而知
以及
。 （iii）
，进而可以用相似求方幂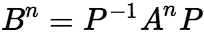
（6）若
，且A，B都可逆，则
。 （7）若
，则
。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
