(1/3) 二次型及其矩阵表示
(1)二次型的定义: 含有n个变量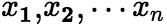 的二次齐次多项式函数(即每项都是二次的多项式)
的二次齐次多项式函数(即每项都是二次的多项式)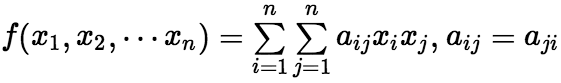 称为n元二次型。 (2)二次型的矩阵表示 令
称为n元二次型。 (2)二次型的矩阵表示 令 ,A=
,A=![]() ,则二次型可用矩阵乘法表示为
,则二次型可用矩阵乘法表示为  其中A是n阶实对称矩阵(
其中A是n阶实对称矩阵( ),称A为二次型
),称A为二次型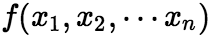 的矩阵,矩阵A的秩r(A)称为二次型f的秩,记作r(f). 注:二次型矩阵是实对称矩阵,且二次型的矩阵是唯一的。
的矩阵,矩阵A的秩r(A)称为二次型f的秩,记作r(f). 注:二次型矩阵是实对称矩阵,且二次型的矩阵是唯一的。
(2/3) 二次型的标准形
(1)二次型标准形的定义 如果二次型矩阵中只含有变量的平方项,所有混合项 的系数全是零,即
的系数全是零,即
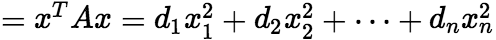 ,其中
,其中 为实数,则称这样的二次型为标准形。 (2)二次型的标准形与矩阵特征值的关系 任意的n元二次型
为实数,则称这样的二次型为标准形。 (2)二次型的标准形与矩阵特征值的关系 任意的n元二次型![]() 都可以通过坐标变换
都可以通过坐标变换 (注意C是可逆矩阵)化成标准形,即
(注意C是可逆矩阵)化成标准形,即 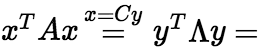
 其中
其中 。特别的,存在正交变换x=Cy化
。特别的,存在正交变换x=Cy化![]() 为标准形,即
为标准形,即 ,
, , 这里
, 这里 是二次型矩阵的n个特征值。 注:二次型
是二次型矩阵的n个特征值。 注:二次型 在线性变换x=Cy下有
在线性变换x=Cy下有
(3/3) 化二次型为标准形的方法
(1)用正交变换化法化二次型为标准形的步骤为: 第一步:把二次型表示为矩阵形式![]() ; 第二步:求A的特征值及其相应的特征向量,(当
; 第二步:求A的特征值及其相应的特征向量,(当 时,检验所求的
时,检验所求的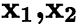 是否正交); 第三步:若特征根有重根,对重根所求的特征向量进行检验,若不正交,则需要利用Schmidt正交化; 第四步:把特征向量单位化
是否正交); 第三步:若特征根有重根,对重根所求的特征向量进行检验,若不正交,则需要利用Schmidt正交化; 第四步:把特征向量单位化 ; 第五步:构造正交矩阵C=
; 第五步:构造正交矩阵C= 第六步:令x=Cy,得
第六步:令x=Cy,得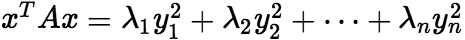 [例题] 用正交变换化二次型
[例题] 用正交变换化二次型 为标准形,并写出所用正交变换。 解:二次型矩阵是
为标准形,并写出所用正交变换。 解:二次型矩阵是 由特征多项式
由特征多项式 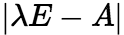
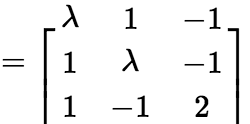

 得到A的特征值是3,-1,0。 对
得到A的特征值是3,-1,0。 对![]() ,由(3E-A)x=0,即
,由(3E-A)x=0,即 解得
解得 。 类似地,对
。 类似地,对 ,
, ;
;![]() 时,
时,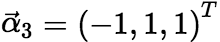 ,特征根无重根,仅需单位化;
,特征根无重根,仅需单位化; 

 构造正交矩阵
构造正交矩阵 , 那么令x=Cy,二次型
, 那么令x=Cy,二次型 为所求标准形。 (2)用配方法化二次型为标准形 用配方法化二次型为标准形的步骤为: 第一步:如二次型中至少有一个平方项,不妨设
为所求标准形。 (2)用配方法化二次型为标准形 用配方法化二次型为标准形的步骤为: 第一步:如二次型中至少有一个平方项,不妨设 ,则对所有含有
,则对所有含有![]() 的项配方,配方后各余项不再含有
的项配方,配方后各余项不再含有![]() ,继续配方,直到每一项都包含在各完全平方项中,引入新变量
,继续配方,直到每一项都包含在各完全平方项中,引入新变量 ,由
,由 ,得到
,得到 。 第二步:如二次型中不含平方项,只有混合项,不妨设
。 第二步:如二次型中不含平方项,只有混合项,不妨设 ,则可令
,则可令 
 经过此坐标变换,二次型中出现
经过此坐标变换,二次型中出现 后,再按第一步进行配方。 注:正交变换法化二次型为标准形时,标准形中平方项系数必须是矩阵A的n个特征值,而配方法没有这个属性。
后,再按第一步进行配方。 注:正交变换法化二次型为标准形时,标准形中平方项系数必须是矩阵A的n个特征值,而配方法没有这个属性。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















