信息资源配置效率的评价标准

2.1.3　信息资源配置效率的评价标准

在本书所做的关于信息资源配置效率的全部研究中，“效率”一词始终隐含“经济效率(economic efficiency)”这样一层解释。要想取得信息资源配置最大化的经济效率，不管在什么样的经济体制下，都要求在不同的生产目的之间合理地分配和使用有限的信息资源(包括妥善处理好信息资源与其他经济资源之间的关系)，最大限度地满足人们的各种需要。因此，如同其他经济资源一样，在信息资源配置过程中必须回答“生产什么”、“生产多少”、“如何生产”、“如何分配”以及“向谁分配”的问题。可见，提高信息资源配置效率，就是要在经济活动中的各种信息资源的各种不同的使用方向之间，分出轻重缓急，决定各种生产性资源的合理选择和安排、生产规模和生产方式的选择和安排等，并寻求一种最佳的分配方式，以实现社会福利最大化。信息资源最优配置是信息资源配置有效率的一个最佳状态，它意味着经济活动的每一种信息资源都能有效地配置于最适宜的地方。我们在研究信息资源配置时，所强调的主要是效率问题。因为信息资源配置活动本身主要是一种市场经济活动，它首先要求根据市场主体的需求来配置资源，以此满足或是保证信息资源配置效率的优化。只有其配置效率高，才能最大化社会福利，有利于整个社会的发展。

在信息资源配置过程中，当某种资源配置格局形成后，人们往往需要对该格局是否有效率做出客观、公正的评价，以决定是否有必要重新进行调整和优化。评价，就其本质而言，无非是主观标准与客观实际情况一致性程度的比较和判断。具体来说，就是人们依据其自身的价值观或道德观建立一套标准，对客观对象进行质和量的比较，并在此基础上做出恰如其分的判断。值得注意的是，由于各人的价值观或道德观不同，因此所建立的标准也就因人而异。正因为如此，能否建立一套为社会公认的评价标准，就成了能否有效配置信息资源的关键。

显然，要在众多因人而异的评价标准中提炼出一套为社会公认的标准是相当困难的。幸运的是，主观的评价标准虽然因人而异，但从最一般的观点出发，社会的某些愿望还是相当明显和趋于一致的，那就是，有效率的信息资源配置意味着社会福利达到最大化。按照这一思想，假如现实的经济生活中出现了下列情况之一，则信息资源配置肯定没有达到“有效率”的状态:

①部分信息产品滞销或脱销。

②低效率的生产者得到较多的信息资源。

这样，评价资源配置是否有效率的问题就可以转化为社会福利是否达到最大化的问题。由意大利经济学家帕累托(V.Pareto)提出的“帕累托最优”标准可称得上是这种评价思想的杰出代表。

作为衡量资源配置效率的基本评价标准，“帕累托最优”指的是这样一种资源配置状态:生产资源的任何重新配置都不可能使一个人的处境变好而又不使另一个人的处境变坏。也就是说，在给定的技术和消费者偏好下，如果不使一个人的满足水平下降，便不可能使其他人的满足水平提高。反过来，如果改变资源配置格局会使每个人的处境都较以前变好了，或者至少一个人的处境变好而没有一个人的处境变坏，则表明资源配置并没有达到“帕累托最优”，或者说资源配置是低效率或无效率的。此时，有必要进行相应的变革，如重新调整存量资源的使用方向、启用增量资源等，从而提高资源配置的效率。

利用“帕累托最优”标准，可以对资源配置状态的任意变化进行“好”与“坏”的判断:如果既定的资源配置状态的任意改变使得社会中至少有一个人的状况变好，同时又没有其他人的状况变坏，则认为这种资源配置状态的变化是“好”的;否则就是“坏”的。用福利经济学的观点来解释，“帕累托最优”实际上就是指社会福利达到最大。以“帕累托最优”标准衡量为“好”的状态改变被称为“帕累托改进”。“帕累托改进”是指这样一种状态，即一项社会变革使得一部分人的社会福利增加的同时，并不减少其他社会成员的福利。对于某种既定的资源配置状态，如果一项社会政策变革使得所有社会成员的福利都有所改善，则该项改革是最理想的;如果一项社会政策变革，在增加一部分社会成员福利的同时，给另一部分社会成员的福利造成不利的影响，则该项改革是否可取，就很难确定。如果对于某种既定的资源配置状态，所有的“帕累托改进”均不存在，则意味着资源配置已处于“帕累托最优”状态。

“帕累托最优”是一种理想境界，可作为一个判断社会经济资源配置状态的标准，而不一定是指现实中的资源配置状态。

就目前已有的研究成果来看，“帕累托最优”虽然最早被用于衡量传统资源的配置效率，但同样也被越来越多的学者认为是衡量信息资源配置效率的基本评价标准，“帕累托改进”也经常被用来泛指信息资源配置效率的优化过程。

霍国庆^[11]、黄丽霞^[12]等认为，信息资源配置的效率主要表现在以下三个方面:一是投资的效率;二是信息需求的效率，是投资效率的具体化;三是信息资源效率，它既是衡量信息资源配置效率的另一个指标，又是投资效率的另一个侧面。

孙瑞英和马海群^[13]则提出了如何综合衡量信息资源配置效率的问题。他们认为信息资源配置一方面必须服从于总体社会资源优化配置和社会福利最大化的宏观目标，另一方面又必须立足于信息生产、信息服务有效的微观基础。首先，宏观上要求整个社会的信息资源配置是有效率的;其次，要求个别信息企业的投入——产出效率是高效率的，同时X效率对所有信息机构的发展也至关重要;第三，在考虑信息资源配置的效率问题时，还要考虑平等的问题，即在追求效率的同时，应兼顾平等。

别传武在其博士学位论文中提到，^[14]衡量信息资源配置效率需要从宏观(总体)、中观(产业)和微观(生产者和消费者)三个不同的层次加以考察。他进一步认为，这种理解主要只是考察非智力型信息资源的配置层次与效率，还存在另外的角度，即考虑智力型信息资源的配置效率。这样就存在着文化或制度的效率、教育的效率、人力资本的效率和信息资源的效率。

1.“帕累托最优”的条件

达到“帕累托最优”状态需要具备一些条件，包括交换领域的“帕累托最优”条件、生产领域的“帕累托最优”条件以及交换和生产领域的“帕累托最优”条件。这三个领域的条件同时满足才意味着资源配置达到了“帕累托最优”状态。下面我们通过埃奇沃斯盒状图(Edgeworth box diagram)来分析各个领域的具体表现。埃奇沃斯盒状图是英国经济学家埃奇沃斯(F.Y.Edgeworth)于19世纪末建立的。盒子的长和高分别代表两个消费者(或生产者)所拥有的两种产品(或生产要素)的总量，盒状图中各点表示两种产品(或要素)的总供给量在两个消费者(生产者)之间的配置状态。埃奇沃斯盒状图揭示了当所有消费的总量或经济活动中使用的投入品总量固定时，如何配置稀缺的经济资源。

(1)交换领域的“帕累托最优”条件

交换领域的“帕累托最优”是指消费者之间产品的最优分配，它是通过产品交换实现的。

假设初始状态下社会只有两个消费者(假设分别为A、B)，他们分别拥有一定数量的产品(假设其数量分别为X、Y)。现在，A、B想通过相互之间交换产品X和Y来改善其福利水平，以实现每个人的福利最大化。

图2-1 是交换的埃奇沃斯盒状图。由于个人福利是通过个人的效用水平来衡量的，所以，实现每个人的福利最大化实际上就是要使每个人的效用达到最大化。

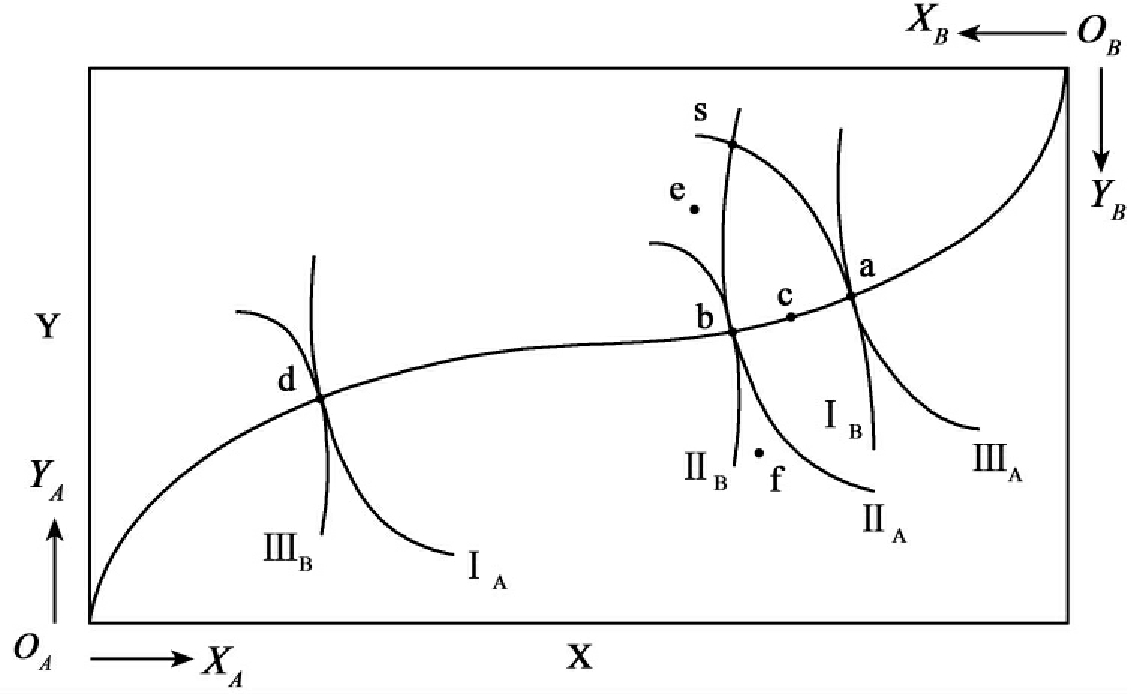
图2-1　交换的埃奇沃斯盒状图

图中，盒子的水平长度表示整个经济中第一种产品的数量X，盒子的垂直高度表示整个经济中第二种产品的数量Y。O_A为第一个消费者A的原点，O_B为第二个消费者B的原点。从O_A出发，水平向右测量消费者A对第一种产品X的消费量X_A，垂直向上测量其对第二种产品Y的消费量Y_A;从O_B出发，水平向左测量消费者B对第一种产品X的消费量X_B，垂直向下测量其对第二种产品Y的消费量Y_B。

考虑盒中的任意一点s，则s对应于消费者A、B，必有式2-1成立:

X_A+X_B=XY_A+Y_B=Y　　　　　　　(2-1)

也就是说，盒中任意一点确定了一组数据，这些数据揭示出每一个消费者对每一种产品的消费情况，而且满足上式要求。可见，埃奇沃斯盒状图中的盒子(包括盒子的边界)确定了两种产品在两个消费者之间的所有可能的分配情形的集合。

为了考察埃奇沃斯盒状图中符合“帕累托最优”状态的点，进一步引入无差异曲线(indifference curve)。无差异曲线是一条表示线上所有各点两种产品不同数量组合给消费者带来的满足程度相同的线。无差异曲线凸向原点，是一条向右下方倾斜的线，表明为实现同样的满足程度，增加一种产品的消费，必须减少另一种产品的消费。在同一个平面上可以有无数条不相交的无差异曲线。

图中，Ⅰ_A、Ⅱ_A、Ⅲ_A是消费者A的三条无差异曲线。其中，Ⅲ_A代表较高的效用水平，Ⅰ_A代表较低的效用水平。从O_A点向右移动，标志着消费者A的效用水平增加;Ⅰ_B、Ⅱ_B、Ⅲ_B是消费者B的三条无差异曲线。其中，Ⅲ_B代表较高的效用水平，Ⅰ_B代表较低的效用水平。从O_B点向左移动，标志着消费者B的效用水平增加。

仍然考虑盒中的任意一点，它揭示了两种产品在两个消费者之间的一种可能的初始分配情形。该点必然处于消费者A的某条无差异曲线上，同时也处于消费者B的某条无差异曲线上。换而言之，该点可能是这两条无差异曲线的交点，也可能是切点。

先考察初始分配状态处于两条无差异曲线的交点的情形，如两条无差异曲线Ⅱ_A、Ⅰ_B相交于s点。容易发现，s点不可能是“帕累托最优”点。因为通过改变初始分配状态，例如从s点变动到a点，则消费者A的效用水平从无差异曲线Ⅱ_A提高到Ⅲ_A，而消费者B的效用水平仍然维持在无差异曲线Ⅰ_B上。因此，在点s仍然存在“帕累托改进”的余地。类似地，从s点变动到b点，则消费者B的效用水平从无差异曲线Ⅰ_B提高到Ⅱ_B，而消费者A的效用水平仍然维持在无差异曲线Ⅱ_A上;从s点变动到c点，则消费者A和B的效用水平均会提高。可见:在交换的埃奇沃斯盒状图中，任意一点，如果它处于消费者A和B的两条无差异曲线的交点上，则就不是“帕累托最优”点，因为在这种情况下，总存在“帕累托改进”的余地。

接着考察初始分配状态处于两条无差异曲线的切点的情形，如两条无差异曲线Ⅱ_A、Ⅱ_B相切于b点。容易发现，b点是“帕累托最优”点。因为b点的任何变动，均不可能存在“帕累托改进”的余地。例如将b点向右上方移动，则消费者A的效用水平提高了，但消费者B的效用水平却下降了;将b点向左下方移动，则消费者B的效用水平提高了，但消费者A的效用水平却下降了;将b点移到e点或f点，则消费者A和B的效用水平均会下降。可见:在交换的埃奇沃斯盒状图中，任意一点，如果它处于消费者A和B的两条无差异曲线的切点上，则是“帕累托最优”点，因为在这种情况下，不存在任何“帕累托改进”的余地。

所有无差异曲线的切点的轨迹构成一条曲线，称做交换契约曲线，它代表两种产品在两个消费者之间分配的所有“帕累托最优”点的集合。由于无差异曲线切点的条件是在该点上的两条无差异曲线的斜率相等，而无差异曲线的斜率的绝对值又称作两种产品的边际替代率(marginal rate of substitution)，因此，交换领域的“帕累托最优”条件可以表述成:当两个消费者对两种产品的边际替代率相等时，就认为在交换领域实现了“帕累托最优”。此时，两个消费者的效用都达到最大化，即所有能够为交换主体带来利益的交换都已发生，在个人之间不存在进一步发生交换的可能性。用公式表示为:

式中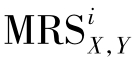，为对i(i为A或B)消费者而言，在维持满足程度不变的前提下，为增加一个单位的X产品而需要相应减少Y产品的消费量。

交换领域达到“帕累托最优”意味着所有消费者的福利都达到了最大。此时，任何消费者都无法在不损害他人福利的前提下通过继续交换提高自己的福利。

交换领域的“帕累托最优”条件是通过竞争性市场的价格机制实现的。在决定是否购买某种产品时，人们往往将从一个单位产品中得到的好处即效用，与获得该产品需要支付的成本即价格进行比较，交换成功意味着消费者得到了超过价格所度量的边际效用。此时，对价格机制的任何限制，均可能导致交换领域缺乏效率。

(2)生产领域的“帕累托最优”条件

生产领域的“帕累托最优”指生产者之间投入的最优配置，它是通过生产要素在不同生产者之间的投入实现的。

假设初始状态下社会只有两个生产者，分别为C、D;两种生产要素，其数量分别为L、K。下面我们用生产的埃奇沃斯盒状图(见图2-2)来探讨两种生产要素L、K在两个生产者C、D之间分配的情况，进而分析生产领域的“帕累托最优”条件。

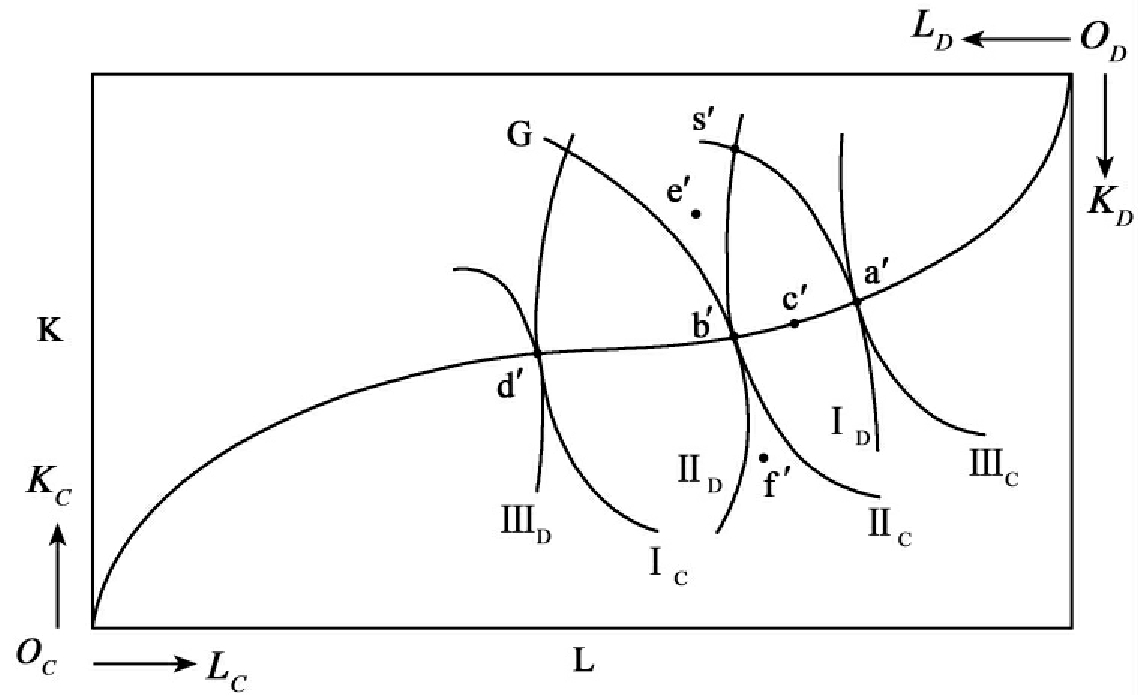
图2-2　生产的埃奇沃斯盒状图

图中，盒子的水平长度表示整个经济中第一种生产要素的数量L，盒子的垂直高度表示整个经济中第二种生产要素的数量K。O_C为第一个生产者C的原点，O_D为第二个生产者D的原点。从O_C出发，水平向右测量生产者C对第一种生产要素L的生产投入量L_C，垂直向上测量其对第二种生产要素K的生产投入量K_C;从O_D出发，水平向左测量生产者D对第一种生产要素L的生产投入量L_D，垂直向下测量其对第二种生产要素K的生产投入量K_D。

考虑盒中的任意一点s'，则s'对应于生产者C、D，必有式2-3成立:

L_C+L_D=L　　K_C+K_D=K　　　　　　　(2-3)

也就是说，盒中任意一点确定了一组数据，这些数据揭示出每一个生产者对每一种生产要素的生产投入情况，而且满足上式要求。可见，埃奇沃斯盒状图中的盒子(包括盒子的边界)确定了两种生产要素在两个生产者之间的所有可能的分配情形的集合。

为了考察埃奇沃斯盒状图中的符合“帕累托最优”状态的点，进一步引入等产量线(isoquant curve)。等产量线是指技术水平不变的条件下生产同一产量的两种生产要素投入量的所有不同组合的轨迹。等产量线凸向原点，是一条向右下方倾斜的线，表明为保持等产量，一种生产要素投入的增加是以另一种生产要素投入的减少作为前提的。在生产要素空间中，可以有无数条不相交的等产量线，它们分别代表了各种特定产量下生产要素L和K的不同数量的组合。距原点越远，等产量线所示的产量就越大。

图中，Ⅰ_C、Ⅱ_C、Ⅲ_C是生产者C的三条等产量线。其中，Ⅲ_C代表较高的产量水平，Ⅰ_C代表较低的产量水平。从O_C点向右移动，标志着生产者C的产量水平增加;Ⅰ_D、Ⅱ_D、Ⅲ_D是生产者D的三条等产量线。其中，Ⅲ_D代表较高的产量水平，Ⅰ_D代表较低的产量水平。从O_D点向左移动，标志着生产者D的产量水平增加。

仍然考虑盒中的任意一点，它揭示了两种生产要素在两个生产者之间的一种可能的初始分配情形。该点必然处于生产者C的某条等产量线上，同时也处于生产者D的某条等产量线上。换而言之，该点可能是这两条等产量线的交点，也可能是切点。

先考察初始分配状态处于两条等产量线的交点的情形，如两条等产量线Ⅱ_C、Ⅰ_D相交于s'点。容易发现，s'点不可能是“帕累托最优”点。因为通过改变初始分配状态，例如从s'点变动到a'点，则生产者C的产量水平从等产量线Ⅱ_C提高到Ⅲ_C，而生产者D的产量水平仍然维持在等产量线Ⅰ_D上。因此，在点s'仍然存在“帕累托改进”的余地。类似地，从s'点变动到b'点，则生产者D的产量水平从等产量线Ⅰ_D提高到Ⅱ_D，而生产者C的产量水平仍然维持在等产量线Ⅱ_C上;从s'点变动到c'点，则生产者C和D的产量水平均会提高。可见:在生产的埃奇沃斯盒状图中，任意一点，如果它处于生产者C和D的两条等产量线的交点上，则就不是“帕累托最优”点，因为在这种情况下，总存在“帕累托改进”的余地。

接着考察初始分配状态处于两条等产量线的切点的情形，如两条等产量线Ⅱ_C、Ⅱ_D相切于b'点。容易发现，b'点是“帕累托最优”点。因为b'点的任何变动，均不可能存在“帕累托改进”的余地。例如将b'点向右上方移动，则生产者C的产量水平提高了，但生产者D的产量水平却下降了;将b'点向左下方移动，则生产者D的产量水平提高了，但生产者C的产量水平却下降了;将b'点移到e'点或f'点，则生产者C和D的产量水平均会下降。可见:在生产的埃奇沃斯盒状图中，任意一点，如果它处于生产者C和D的两条等产量线的切点上，则是“帕累托最优”点，因为在这种情况下，不存在任何“帕累托改进”的余地。

所有等产量线的切点的轨迹构成一条曲线，称做生产契约曲线，它代表两种生产要素在两个生产者之间分配的所有“帕累托最优”点的集合。由于等产量线切点的条件是在该点上的两条无差异曲线的斜率相等，而无差异曲线的斜率的绝对值又称做两种产品的边际技术替代率(marginal rate of technical substitution)。一种生产要素对另一种生产要素的边际技术替代率是指在生产技术水平不变的条件下，维持同样的产量，增加一个单位的某种生产要素可以替代另一种生产要素的数量。因此，生产领域的“帕累托最优”条件可以表述成:对于两个生产者来说，当两种生产要素的边际技术替代率相等时，就认为在生产领域实现了“帕累托最优”。此时，两个生产者的产量都达到了最大化，即不可能生产出更多某些产品而不减少其他产品的产量。

对于生产者C和D，若L代替K的边际技术替代率分别用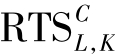和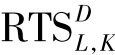来表示，则生产领域的“帕累托最优”条件可以用公式表示为:

当生产领域达到“帕累托最优”时，任何生产者都无法在不损害他人福利的前提下通过重新调整生产要素在不同使用方向上的分配来提高自己的福利。

(3)交换和生产领域的“帕累托最优”条件

交换领域和生产领域分别达到了“帕累托最优”还不能表明资源配置实现了“帕累托最优”。因为交换领域的最优只是说明消费是最有效率的，生产领域的最优只是说明生产是最有效率的。在这种情况下，还是有可能通过交换和生产领域的重新组合提高社会福利，例如在维持消费者满足程度不变的情况下提高产出水平，或者在维持产出水平不变的情况下提高消费者的满足程度，或者使消费者的满足程度和产出水平都提高等。交换和生产领域的“帕累托最优”正是就这两个领域的综合而言的。

我们将前面关于交换和生产的假设合并起来，即:假设整个经济只包括两个消费者A和B，他们在两种产品X和Y之间进行选择，以及两个生产者C和D，他们在两种生产要素L和K之间进行选择以生产两种产品X和Y(假设C生产X，D生产Y)。

我们引入生产可能性曲线(production possibilities curve)。生产可能性曲线用来表示经济社会在既定资源和技术条件下所能生产的各种产品最大数量的组合，反映了资源稀缺性与选择性的经济学特征。如图2-3所示，PP'为生产可能性曲线，它向右下方倾斜且向右上方凸出。

在生产可能性曲线上任意选一点(如B点)。根据生产可能性曲线的性质，该点是生产契约曲线上的一点，满足生产的“帕累托最优”条件;同时，该点又表示一对产出的最优组合，即(X₀，Y₀)。从B点出发，分别引一条垂直线到X₀和一条水平线到Y₀，则得到一个矩形AY₀BX₀A，该矩形对应着交换的埃奇沃斯盒状图:矩形的水平长度表示整个经济中第一种产品的数量X₀，垂直高度表示整个经济中第二种产品的数量Y₀;A为第一个消费者A的原点，B为第二个消费者B的原点;矩形中任意一点表示既定产出X₀和Y₀在两个消费者之间的一种分配情形。

根据前面的分析，埃奇沃斯盒状图AY₀BX₀A中交换契约曲线上的每一点均为交换的“帕累托最优”点。因此，给定生产契约曲线上的一点(即给定一个生产的“帕累托最优”点)，便有一条交换契约曲线(即有无穷多个交换的“帕累托最优”点)与之对应。在这条交换契约曲线上的任意一点(如C点)，均表示交换在单独看时已处于“帕累托最优”状态，但并不一定表示在与生产联合起来看时也处于“帕累托最优”状态。

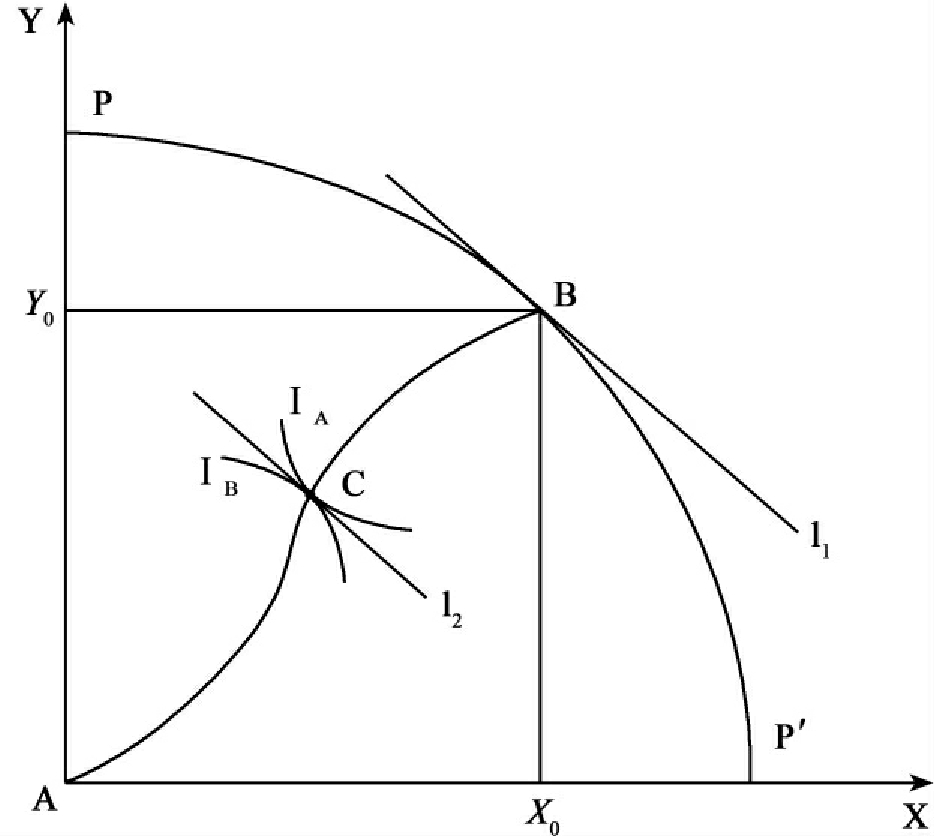
图2-3　交换和生产领域的“帕累托最优”

在上图中，生产可能性曲线上的B点的切线l₁的斜率的绝对值是产品X在该点上转换为产品Y的边际转换率(marginal rate of transformation)，交换契约曲线上的C点是无差异曲线Ⅰ_A和Ⅰ_B的切点。Ⅰ_A和Ⅰ_B的共同切线l₂的斜率的绝对值是产品X在该点上替代产品Y的边际替代率。切线l₁和l₂可能平行，也可能不平行。即:产品的边际转换率与边际替代率可能相等，也可能不等。可以证明，如果边际转换率与边际替代率不相等(边际转换率大于或小于边际替代率)，则意味着未达到交换和生产的“帕累托最优”状态，因为此时仍存在着“帕累托改进”的余地，社会福利会因某种努力而增加。由此，可以得出交换和生产领域的“帕累托最优”条件为:两种产品在交换中的边际替代率等于在生产中的边际转换率。用公式表示为:

MRS_X，Y=MRT_X，Y　　　　　　　　(2-5)

式中，MRT_X，Y为边际转换率，表示在既定的技术和资源条件下，为增加一个单位的X产品而需要相应减少Y产品的产出量。MRS_X，Y为边际替代率，表示在维持满足程度不变的前提下，为增加一个单位的X产品而需要相应减少Y产品的消费量。

交换和生产领域达到“帕累托最优”，意味着不仅要求交换在“帕累托最优”状态下进行，而且要求生产也要实现“帕累托最优”，即生产者之间的投入配置与消费者之间的产品分配都达到最优状态。

需要说明的是，前面对交换领域、生产领域以及交换和生产领域“帕累托最优”条件的讨论，是以整个经济中只有两个消费者、两种产品、两个生产者、两种生产要素为假设前提的，它同样也适用于多个消费者、多种产品、多个生产者、多种生产要素的一般情况。^[15]

2.完全竞争市场与“帕累托最优”的实现

亚当·斯密(Adam Smith)曾断言:经济组织或个人在追求各自的私利的同时，会在一只“看不见的手”的指挥下，去尽力达到一个并非其本意想达到的增进社会福利的社会目的。^[16]也就是说，市场机制像一只“看不见的手”能自动引导资源向最有效率的方向配置。当代西方经济学家将亚当·斯密的这一思想发展成为一个更加精致的“定理”:给定一些理想条件，经济组织或个人在完全竞争经济中的最优化行为将导致“帕累托最优”状态。

根据福利经济学的观点，完全竞争市场的一般均衡状态就是“帕累托最优”状态。也就是说，完全竞争市场的一般均衡符合“帕累托最优”所需要的条件，因而完全竞争市场的一般均衡就是“帕累托最优”状态。这就是福利经济学第一定理。该定理不仅说明了完全竞争市场经济的优越性，而且也反映了福利经济学理论的应用领域和方向。

根据福利经济学第一定理，自由竞争的市场经济体制是最有效的，因为资源配置可以通过价格信号进行灵活调节，并且市场决策由市场主体自主自发进行，具有时效性、目的性以及相关性等特征。

福利经济学第二定理是指，从任一个初始资源配置状态出发，通过市场竞争机制形成的均衡必然可以实现“帕累托最优”状态。也就是说，任意一个“帕累托最优”状态均可以通过市场竞争均衡实现。

完全竞争市场具备以下特点:自由的市场、小规模的经济主体、同质的商品、自由流动的资源、充分的信息。在完全竞争市场中，用户追求最大的效用，生产者追求最大的利润，且任何一个经济行为者(买方或卖方)的行为都不能对市场价格产生直接的影响。在这种情况下，价格是信息供需变化的指示器，价格体系给每个经济行为者提供了关于生产可能性、资源可获得性及所有其他决策者偏好的“信息摘要”。市场上信息供需热点的变化往往以价格信号反馈的方式表现出来，并通过价格体系对资源配置进行优化。

由于完全竞争市场的一般均衡状态就是“帕累托最优”状态，而每一种“帕累托最优”的资源配置格局也总能够通过完全竞争的一般均衡来实现，因此，完全竞争市场机制与资源的有效配置实际上是同一问题的两个不同侧面，用库普曼的话来说，就是“如同一枚硬币的两面”。^[17]即:在一定的条件下，完全竞争市场机制能够实现资源的有效配置，或者说，资源的有效配置可以通过完全竞争市场机制来实现。完全竞争市场机制是完全竞争的均衡状态。在这个状态里，每个消费者的满足达到最大，每个生产者的利润达到最大。

需要说明的是，由于完全竞争市场的上述特点在现实中很难满足，因此，完全竞争市场毕竟只是假想中的理想市场。在当今市场范围极其广泛、交易活动十分复杂、市场规模非常庞大的情况下，现实的市场是不可能具备完全竞争市场特点的，完全竞争的市场几乎是不存在的。也就是说，完全竞争市场的假设在真实世界中并不成立。在现实的经济中，垄断或竞争不完全现象的普遍存在会导致市场失灵，此时，价格体系不再是关于生产可能性、资源可获得性及所有其他决策者偏好的“信息摘要”，从而无法满足“帕累托最优”条件，使资源配置偏离最优配置状态。此外，外部性、公共物品的存在，也会导致类似的结果。关于这一点，我们在本书后续的章节中会作进一步的研究。在现实中，至多存在某些市场特征近似于完全竞争市场的市场，可以按照完全竞争市场的规律来进行分析。

更进一步地，上述论断是否意味着前面所提出的通过完全竞争的一般均衡来实现“帕累托最优”的资源配置格局没有现实意义呢?其实不然，因为完全竞争市场虽然只是一种理想的状况，但它却是整个微观经济分析的基础，借鉴对完全竞争市场的分析，我们还是可以间接地探求不完全竞争市场状态下资源有效配置的基本规律的。那么，现实的市场是否也能通过努力实现资源配置的“帕累托最优”呢?从理论上说是可以的，只不过与完全竞争市场相比，在改善资源配置方案方面需要投入更多的信息搜寻成本和付出更大的努力。^[18]