数据包络分析模型的建立

7.3.2　数据包络分析模型的建立

自从1978年C²R模型提出之后，它在各个领域得到了较多应用。出于研究的需要，不断扩充和完善DEA模型，现已形成巨大的模型集。大体上，这些模型可分为输入模型和输出模型，其中，输入模型研究的是在不减少输出的情况下，考虑输入是否还能减少;输出模型研究的是在不增加输入的情况下，考虑是否还能增加输出。这里，以输入模型为例，分别介绍C²R模型、BC²模型、C²SG²模型等基本模型和一些扩展模型。

1.基本模型

(1)C²R模型与DEA有效性

C²R模型主要用于判断信息资源配置的总体效率，即判断在技术和规模两方面是否同时有效，其中“技术有效”是指输出相对投入而言已达最大，即该决策单元位于生产函数的曲线上;所谓“规模有效”指投入量不偏大，也不过小，是介于规模收益由递增到递减之间的状态，即处于规模收益不变的最佳状态。C²R模型中的DEA有效的决策单元既是规模适当又是技术管理水平高的，它有两种表达形式:一种是最初基于工程效率的比率定义提出的分式规划形式，另一种是由分式规划变化而来的线性规划形式。

在实际评价时，假设有n个决策单元(DMU)，每个DMU都有m种输入和s种输出，分别用X_j=(x_1j，x_2j…x_mj)^T＞0，Y_j=(y_1j，y_2j…y_rj)^T＞0来表示，其中j=1，2…n。X_ij表示对第i种输入的投入量，Y_rj表示对r种输出的产出量(i=1，2…m;r=1，2…s)。为方便，记DMU_j0对应的输入、输出数据分别为X₀=X_j0，Y₀=Y_j0，1≤j₀≤n，评价DMU_j0的DEA分式规划模型(C²R)为:

其中，v=(v₁，v₂…v_m)^T，u=(u₁，u₂…u_s)^T

令，ω=tv，μ=tu，可将分式形式的(C²R)^I转化为等价的线性规划:

线性规划的对偶规划为:

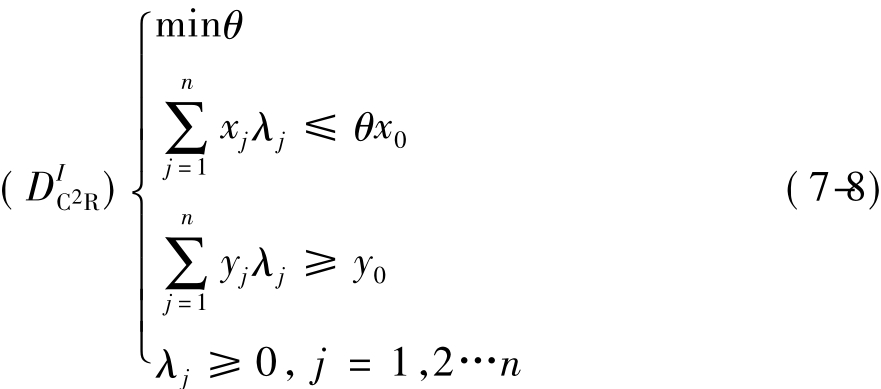
其中，θ∈E¹

利用和判断DMU的DEA有效性并不直接，Charnes和Cooper给出了具有非阿基米得无穷小ε的DEA模型:

其中，，e(1，1…1)∈E^s，λ_j为一般变量，m为输入指标数，r为输出指标数，未知量s^-，s⁺为松弛变量，θ为C²R模型的最优解，ε为非阿基米得无穷小量。设C²R模型的最优解为λ⁰，s^-0，s⁺⁰，θ⁰，则有以下结论。

当θ⁰=1时，则DMU_j0为弱DEA有效;说明在不减少信息资源配置产出的情况下，无法等比例地减少各种消耗，但可以把用于配置的某项资源消耗减少s^-仍可保持原产出不变，或是在消耗资源不变的情况下将某项产出提高s⁺。

当θ⁰=1，s^-0=0，s⁺⁰=0时，DMU_j0为DEA有效;说明在不减少信息资源配置产出的情况下，无法等比例地减少各种消耗，也不能单独减少某种资源消耗或增加某项产出，相对其他弱DEA有效和非DEA有效的信息资源配置单元来说，其运作绩效是最好的，消耗与产出比最优，规模也是最适合的。

利用C²R模型也可以判断信息资源配置是否规模有效，即判断其规模收益是递增、递减还是不变。当时，DMU_j0规模收益不变;说明规模收益递增，说明规模收益递减。

(2)BC²模型与技术有效

规模报酬不变条件下的C²R模型隐含着DMU可以通过增加投入等比例地扩大产出规模，即DMU规模的大小不影响其效率。对于信息资源配置来说，这一假设相当严格，信息市场的不完全竞争、经济环境以及信息产业政策等因素都可能导致DMU难以在理想化的规模下运行，因此规模收益不变的假设不符合信息资源配置实际。在C²R模型中增加限制条件，即变成BC²模型(C²SG²模型)，主要用于判断被评价单位在目前规模下的技术有效性，具体模型如下:

其中，θ∈E¹

引入非阿基米得无穷小ε后，原DEA模型为:

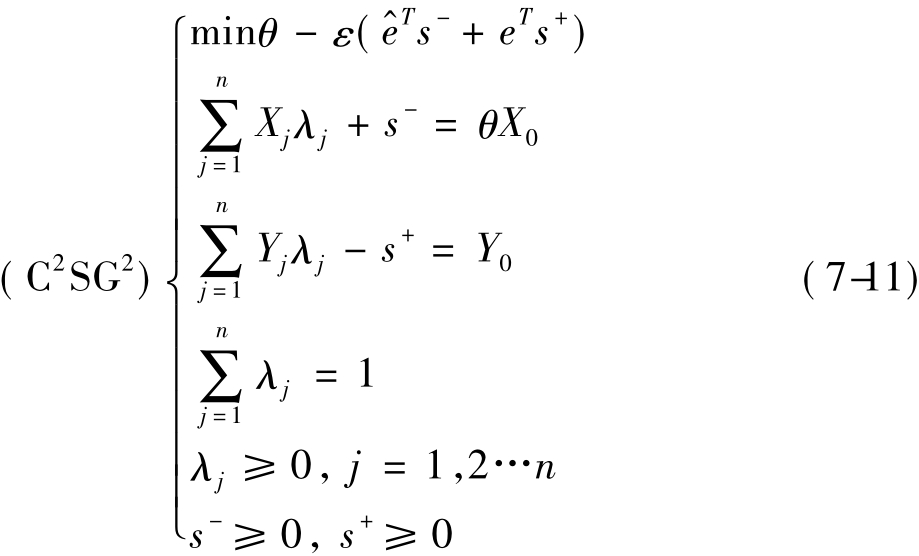
上述两个模型放松了规模报酬不变的假设，利用两者都可以计算出每个信息资源配置单元(DMU)的技术效率，而得到技术有效的DMU和技术无效的DMU，技术有效是指输出相对投入而言已达最大，即位于生产函数曲线上的被评价单元;反之，技术无效是指在不减少信息资源配置产出的情况下，可等比例地减少各种消耗，或是在不增加消耗的情况下，等比例增加各种产出。而规模收益这一概念主要是用来评价在一个生产过程中，投入增量相对百分比与对应的产出增量相对百分比究竟哪个大。由于规模效率=整体效率/技术效率，分别利用C²R和BC²(C²SG²)可计算出规模效率情况:若求得规模效率大于1说明对应的DMU规模收益递减，应该加大投资规模;相反，规模效率小于1，则说明对应的DMU规模收益递增，应减少各种资源的投入;当整体效率和技术效率相等时，说明该DMU是规模有效的，即规模收益不变。

2.扩展模型

从DEA模型的发展来看，DEA方法中两个最基本的模型是C²R模型和BC²模型。这两个模型的产生不仅扩大了人们对生产理论的认识，而且为评价多目标问题提供了有效的途径，使得研究生产函数理论的主要技术手段由参数方法发展成为参数与非参数方法并重。为了发展和完善DEA理论，使之更加符合客观现实的需要，人们在这两个模型的基础上，又发展了一些新的DEA模型，主要有以下几个类型。

(1)含有偏好的DEA模型

就DEA模型本身的特点而言，m种输入指标和s种输出指标在评价DMU的有效性时，所处的地位是等同的。各被评DMU输入、输出向量对应的权重是通过效率指数进行优化来决定的，每个评价对象都可以选取对它最有利的权向量。这一方面有利于处理那些输入、输出之间权重信息不清楚的问题，另一方面也有利于排除对权重施加某些主观随意性。但是，自从DEA第一个模型公开后，从事多目标决策的人就曾经提出过异议，认为DEA模型没有体现决策者的偏好。

A.Charnes、W.W.Cooper和魏权龄等人在1986年给出了一个含偏好的DEA模型——C²WH模型，^[15]该模型将偏好锥引进到DEA模型中，可以反映决策者的偏好，使得决策更能反映人的意愿。随后，A.Charnes等人又对C²WH模型做了一系列的推广，得到了具有锥结构的综合DEA模型，具有锥结构的离散DEA模型^[16]。该模型通过选取一定的权重系数，来确定各输入、输出指标的变化率，以获得令决策者满意的投影点，即DEA有效前沿面上的一个有效投影点。

(2)具有无穷多个DMU的DEA模型

原始的DEA模型是针对DMU有限的情况下进行讨论的，为了解决具有无限个决策单元的评价问题，A.Charnes、W.W.cooper和魏权龄等人利用半无限规划理论将C²R模型推广到具有无限多个DMU的情况，给出了C²W模型。该模型是国际上第一个非线性的DEA模型，它深刻地揭示了DEA在数学上和经济上的含义，被认为“提出了一个精美的研究结构，并且对DEA随机背景的进一步研究给出了一个简明完好的分析基础”。^[17]

(3)随机DEA模型

传统的DEA模型均假设DMU的输入输出数据精确可测，属于确定性DEA分析方法。但在实践中，由于测量误差、数据噪声、经济现象和经济规律的不确定性等因素，一个决策单元的评价指标往往无法精确确定，而是服从一定概率分布的随机变量。在随机DEA模型这一方面，美国计量经济学家和数理统计学家J.K.Sengupta做了大量的工作，将随机因子引入DEA分析之中，利用各种统计方法对单输出条件下随机DMU的相对有效性进行了深入的探讨。黄志民等人在研究所有的输入、输出均为随机变量时，给出了随机非支配点的概念，由此得到了含有随机因子的线性及非线性的数据包络模型即机会约束的DEA模型，^[18]并对这些数据包络模型解的存在性和规律性进行了讨论，得出了一些有意义的结论。

(4)含模糊因素的DEA模型

DEA评价中的另一类不确定性是评价中的模糊、灰色因素，在评价部门为相对有效性时，诸多的输入输出指标中，不免有一些定性指标难以量化成一个准确的数值。早在1970年，Bellman和Zaeh就研究过模糊决策问题，之后许多学者都对模糊线性规划问题做了研究，但大多数研究的结果都是确定的。2000年，Kao和Liu应用α分割法和Zaeh扩展原理将模糊DEA转化成一系列通常的确定型DEA模型，^[19]并且得到了用隶属函数表示的有效性度量，可以更为真实地反映出DMU的相对有效性。

(5)复合DEA模型

经验与理论都表明DEA方法中选择评价指标的重要性。由于在不同指标下DEA评价结果是不同的，因而随指标变化的DEA有效性变化中所包含的信息具有应用价值。基于这一思想，有学者设计了一种以不同指标下的有效性系数为基础，获取决策单元有效性和输入、输出指标之间关系的信息的方法，对DEA方法进行了推广，从不同指标下的有效性系数中综合出DMU的输入、输出特性的信息。

此外，还有多种其他的DEA模型，如:加法模型、逆DEA模型、动态DEA模型、具有不可控因素的DEA模型以及灰色DEA模型等。